Кривые второго порядка

ГБОУ РХ СПО «Училище (техникум) олимпийского резерва»

Отделение физической культуры

Реферат

Тема: «Кривые второго порядка»

Выполнил:

Студент 282группа

Рец Владимир

Г. Абакан

Содержание

Введение

.Кривые второго порядка

Окружноь

Эллипс

Гипербола

Парабола

Теоремы, связанные с кривыми второго порядка

Ломаная линия

Сплайн Эрмита

Кубический сплайн

Параллельный перенос системы координат

Литература

Введение

Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.

Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.

Кривые второго порядка

Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением

ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0

где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .

Вид кривой зависит от четырёх инвариантов:

инварианты относительно поворота и сдвига системы координат:

инвариант относительно поворота системы координат (полуинвариант):

Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:

Так, например, невырожденная кривая оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:

Или

λ2 − Iλ + D = 0.

Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:

Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.

Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.

Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:

Эллипс

Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.

Если эллипс описывается каноническим уравнением

где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где

Величина e = c/a называется эксцентриситетом эллипса.

По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам

Если фокусы эллипса совпадают, то эллипс является окружностью.

Окружность

ОпределениеОкружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.

Получим уравнение окружности, если известны ее центр и радиус.

ТеоремаОкружность радиуса с центром в точке имеет уравнение

(12.2)

Доказательство. Пусть -- текущая точка окружности. По определению окружности расстояние равно (рис. 12.1)

Рис.12.1.Окружность

По формуле (10.4) для плоскости получаем, что точки окружности и только они удовлетворяют уравнению

Обе части уравнения неотрицательны. Поэтому после возведения их в квадрат получим эквивалентное уравнение (12.2).

Если в уравнении (12.2) раскрыть скобки и привести подобные члены, то вид его изменится. Однако любое уравнение окружности с помощью тождественных преобразований можно привести к виду (12.2). Для этого достаточно выделить полные квадраты по переменным 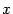и .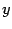

ПримерНарисуйте кривую .

Решение. Выделив полные квадраты, получим

Если выделение полных квадратов вызывает затруднение, то более подробные объяснения можно получить здесь.

Итак, центр окружности -- , радиус равен 2 (рис. 12.2).

Рис.12.2.Окружность, заданная уравнением

Гипербола

Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением

где a > 0, b > 0 — параметры гиперболы.

Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.

В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.

Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.

С осью OY гипербола не пересекается.

Отрезки a и b называются полуосями гиперболы.

Рис.1

Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.

Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).

Рис.2

Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.

Парабола

Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением

y2 = 2 px

где p > 0 — параметр параболы.

Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.

В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.

Рис.3

Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы: