Оценка остаточного члена в формуле Тейлора

Теоремы Ролля, Лагранжа, Коши

Мы продолжаем изучение свойств дифференцируемых функций. Первой мы изучили теорему Ферма, суть которой заключается в том, что в точке экстремума производная функции или не существует, или равна 0.

Теорема 1. (Теорема Ролля) Пусть функция непрерывна на отрезке , имеет производную на интервале и при этом . Тогда существует точка , в которой выполнено условие .

Доказательство. Функция непрерывна на отрезке и, следовательно, достигает на этом отрезке свое наибольшее и наименьшее значения. Если эти значения совпадают, то функция равна константе, и ее производная равна 0 в каждой точке интервала . Если же наибольшее и наименьшее значения функции не совпадают, то хотя бы одно из них не совпадает со значением функции на границах отрезка. Пусть в точке достигается наибольшее или наименьшее значение функции на отрезке . Тогда эта точка является точкой экстремума и в этой точке по теореме Ферма производная равна 0. Теорема доказана.

Теорема 2. (Теорема Лагранжа) Пусть функция непрерывна на отрезке и имеет производную на интервале . Тогда существует точка , в которой выполнено условие , (1)

Формула (1) называется формулой Лагранжа. Иногда ее записывают в виде и называют формулой конечных приращений Лагранжа.

Теорема 3. (Теорема Коши) Пусть функции и непрерывны на отрезке , имеют производные , на интервале и при этом при . Тогда существует точка , в которой выполнено условие (2).

Формула (2) называется формулой Коши.

Доказательство. Заметим, что теорема Лагранжа является частным случаем теоремы Коши, если в качестве функции взять функцию . Для доказательства теоремы Коши рассмотрим вспомогательную функцию . Заметим, что функция непрерывна на отрезке и имеет производную на интервале , при этом . Итак, для функции выполнены все условия теоремы Ролля. Отсюда существует точка , в которой выполнено условие . Следовательно, , что и равносильно условию (2). Теоремы Коши и Лагранжа доказаны.

Правило Лопиталя

Что надо сделать при вычислении предела функции ? Если функция непрерывна, то мы просто подставляем предельное значение. Случаи, когда для вычисления нельзя подставить предельные значения, называются неопределенностями. При вычислении предела вида возможна ситуация, когда и предел числителя, и предел знаменателя равны 0. Ясно, что в этом случае нельзя применить теорему о том, что предел частного равен частному от пределов. Такого рода ситуация называется неопределенностью вида . Если числитель и знаменатель стремятся к бесконечности, то это неопределенность вида . Бывают и другие виды неопределенностей, например, , , . Правило Лопиталя применимо только для неопределенностей вида и . Другие виды неопределенностей могут быть преобразованы к неопределенностям этих видов.

Теорема 4. (Теорема Лопиталя) Пусть функции и определены, непрерывны и дифференцируемы в некоторой окрестности точки , за исключением, быть может, самой точки , при этом предел является неопределенностью вида . Тогда , (3) если предел существует.

Доказательство. Так как и , то функции и можно доопределить условиями . Таким образом доопределенные функции становятся непрерывными на отрезке, соединяющем точки и . Поэтому для отношения применима теорема Коши и, следовательно, существует точка , лежащая на этом отрезке такая, что . Отсюда и следует утверждение теоремы.

Пример 1. Вычислите предел .

Решение. Так как это неопределенность вида , то является законным применения правила Лопиталя. Следовательно, . Ответ. -8.

Сделаем комментарий к этой краткой записи решения примера. Отметим, что, прежде всего, мы проверили, что пределы по отдельности числителя и знаменателя равны 0, т. е. что у нас неопределенность вида . Обратите внимание, что полученный после применения правила Лопиталя предел также является неопределенностью вида . Является ли в этой ситуации законным вторичное применение этого правила? Безусловно, да. По правилу Лопиталя, при соответствующих условиях предел отношения функций равен пределу отношения производных, если предел отношения производных существует. При таких обстоятельствах нам нет необходимости заранее проверять существования предела отношения производных. Поэтому правило Лопиталя можно применять неоднократно, пока не исчезнет неопределенность. В данном случае выражение можно преобразовать к виду и вычислить предел, как предел произведении.

Отметим, что под бесконечно большой величиной понимается величина, обратная к которой является величиной б. м. Отсюда несложно показать, что и к отношению б. б. величин также применимо правило Лопиталя.

Правило Лопиталя. Предел отношения бесконечно малых или бесконечно больших величин равен пределу отношению производных, если предел отношения производных существует.

Пример 2. Вычислите предел .

Решение. Так как это неопределенность вида , то является законным применения правила Лопиталя. Следовательно, . Ответ. 0.

Формула Тейлора

Как мы с вами уже отмечали, рычагом к созданию в 17, 18 веках теории дифференциального исчисления явилось необходимость приближения сложной функции более простыми функциями. В качестве таких простых функций английский математик Брук Тейлор (1685-1731) стал использовать многочлены.

Рассмотрим многочлен степени , определяемый параметрами: . Пусть задана функция , имеющую производных в точке . Рассмотрим чисел: , , , …, . Они однозначно определяют многочлен Тейлора степени не выше , обладающий тем свойством, что , ,…, :

(4)

Многочлен Тейлора (4) и его производных совпадают в точке с функцией и ее производными. Разумно предположить, что многочлен Тейлора (4) приближает функцию в окрестности точки . Этот факт отражается формулой

, (5)

которая называется формулой Тейлора. При формула Тейлора (5) принимает вид (6) и называется формулой Маклорена.

Обратите внимание, что формула Тейлора (5) не нуждается в доказательстве, вопрос состоит лишь в оценке для конкретной функции величины , которая называется остаточным членом в формуле Тейлора. Применение формулы Тейлора разумно в том случае, когда остаточный член является малой величиной и стремится к 0 при . Для непосредственного применения формулы Тейлора необходимо вычислить производные функции в точке .

Пример 3. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

Решение. Так как функция совпадает со всеми своими производными, то выполнено условие 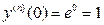и формула (6) принимает вид . (7)

Пример 4. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

Решение. Если , то , , , и далее производные функции повторяются. Значения синуса и его производных в точке 0 соответственно равны числам: 0, 1, 0, -1, 0 и т. д. Это можно записать в виде формул: , , . Следовательно, искомая формула принимает вид . (8)

Пример 5. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

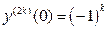Решение. Если , то , , , и далее производные функции повторяются. Значения косинуса и его производных в точке 0 соответственно равны числам: 1, 0, -1, 0, 1 и т. д. Это можно записать в виде формул: , , . Следовательно, искомая формула принимает вид . (9)

Обратите внимание, что формула (9) может быть получена из формулы (8) дифференцированием ее левой и правой частей. И это не случайно. Не обязательно каждый раз вычислять все производные исследуемой функции.

Пример 6. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

Решение. Искомую формулу мы получим, заменив в формуле (7) аргумент на аргумент . Учитывая, что , мы приходим к искомой формуле . (10)

Сопоставляя формулы (7), (8), (9), (10), мы приходим к формуле Эйлера , (11) которая упоминалась в лекции 1. Полностью формула Эйлера будет доказана, когда будет установлено, что в формулах (7), (8), (9) остаточные члены с ростом стремятся к 0 при всех значениях аргумента.

Пример 7. Напишите формулу Тейлора для функции в точке (формулу Маклорена для функции ).

Решение. Если , то , , , , …, ( ). Следовательно, искомая формула принимает вид . (12)

Оценка остаточного члена в формуле Тейлора

Неотъемлемой частью использования формулы Тейлора является оценка ее остаточного члена. Красивые и практичные формулы появлялись в работах выдающихся математиков 18, 19 и да в 20 веках. Отметим некоторые результаты без доказательства.

Теорема 5. (Теорема Лагранжа) Пусть функция имеет в некоторой окрестности точки производную -го порядка. Тогда для произвольной точки из этой окрестности найдется точка , принадлежащая интервалу, соединяющую точки и , обладающую тем свойством, что в формуле (5) выполнено соотношение , (13)

Теорема 6. (Теорема Коши) Пусть функция имеет в некоторой окрестности точки производную -го порядка. Тогда для произвольной точки из этой окрестности найдется точка , принадлежащая интервалу, соединяющую точки и , обладающую тем свойством, что в формуле (5) выполнено соотношение , (14)

Теорема 5. (Теорема Пеано) Пусть функция имеет в некоторой окрестности точки производную -го порядка. Тогда в формуле (5) выполнено соотношение , (15)