Векторное произведение двух векторов

его свойства и применение*

Векторным произведениемвекторов и (рис. 10) называется вектор , удовлетворяющий следующим условиям:

1) модуль вектора равен , где – угол между векторами и , т.е. численно равен площади параллелограмма, построенного на векторах и , как на сторонах;

2) вектор ортогонален векторам и ;

3)векторы , и в указанном порядкеобразуют правую тройку векторов, т.е. если смотреть на векторы и с конечной точки вектора , то кратчайший поворот от к будет осуществляться против часовой стрелки.

Обозначается векторное произведение как ,или .

Векторное произведение векторов обладает следующими свой­ствами:

1. ;

2. , есл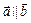и или = , или = ;

3. (l )´ = ´(l )=l( ´ );

4. ´( + ) = ´ + ´ .

В частности, векторное произведение единичных векторов , образующих прямоугольный базис, определяется по следующей схеме (рис. 11):векторное произведение совпадающих сомножителей равно нулю; векторное произведение несовпадающих сомножителей равно третьему не задействованному в произведении орту, взятому с положительным знаком, если направление кратчайшего поворота от первого сомножителя до второго совпадает с направлением часовой стрелки, и со знаком минус в противном случае.

´

В координатной форме векторное произведение векторов 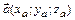и равно:

´ = .

Применение векторного произведения векторов.

1.Проверка векторов на коллинеарность. Если 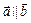, то и наоборот.

Пример 1.Проверить векторы и на коллинеарность.

Решение.Запишем векторы в координатной форме (2; 5; 1), (1; 2;–3)и найдем их векторное произведение:

.

Так как , то эти векторы не коллинеарны.

2. Нахождение площадей параллелограмма и треугольника. Согласно определению векторного произведения векторов и модуль этого произведения численно равен площади параллелограмма, построенного на векторах и , как на сторонах, т.е.

,

а значит площадь соответствующего треугольника будет равна

.

Пример 2. Найти площадь параллелограмма, построенного на векторах , если

Решение. Площадь параллелограмма определяется по формуле

. Найдем .

Тогда (ед.²).

Пример 3. Вычислить площадь треугольника с вершинамиА(2;2;2), В(4; 0; 3),С(0; 1; 0).

Решение.Найдем координаты векторов и :

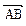или

или .

Тогда

а его модуль равен

Следовательно, площадь треугольника равна (ед.²).

3. Определение момента силы относительно точки.*Пусть в точке А приложена сила и пусть О – некоторая точка пространства (рис. 12).

Из физики известно, что моментом силы относительно точки О называется вектор , который проходит через точку О и удовлетворяет следующим условиям:

1) перпендикулярен плоскости, проходящей через точки О, А, В;

2) численно равен произведению силы на плечо:

;

3) образует правую тройку векторов с векторами и .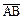

Из вышесказанного можно сделать вывод, что

.

Пример 4.Найти величину момента силы относительно точки , если сила приложена к точке .

Решение.Определим координаты вектора , Момент силы относительно точки А найдем как

, .

Тогда величина момента силы равна модулю вектора .

Литература: [3, гл.2, п. 12.12]; [4, гл. 2, §7].