Линейные диф. уравнения n-го порядка. Теорема об общем решении неоднородного линейного уравнения n-го порядка

Системы линейных диф. уравнений.

Система диф.уравнений называется линейной,если она линейна относительно неизвестных ф-ий и их производных. Систему n-линейных уравнений 1-го порядка записывают в виде:

коэф-ты системы являются const.

Эту систему удобно записывать в матричной форме: ,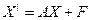

где 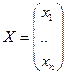- вектор-столбец неизвестных ф-ий, зависящих от одного аргумента.

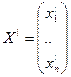- вектор-столбец производных этих ф-ий.

- вектор-столбец свободных членов.

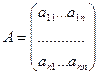- матрица коэффициентов.

Теорема 1: Если все коэф-ты матрицы А непрерывны на некотором промежутке и , то в некоторой окрестности каждой т. 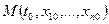выполнены условия ТСиЕ. Следовательно, через каждую такую точку проходит единственная интегральная кривая.

Действительно, в таком случае правые части системы непрерывны по совокупности аргументов и их частные производные по 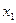(равные коэф-там матрицы А) ограничены, в силу непрерывности на замкнутом промежутке.

Методы решения СЛДУ

1. Систему диф.уравнений можно свести путем исключения неизвестных к одному уравнению.

Пример: Решить систему уравнений: (1)

Решение: исключаем z из данных уравнений. Из первого уравнения имеем 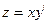. Подставляя во второе уравнение, 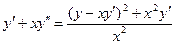получаем после упрощения: .

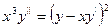Данная система уравнений (1)приведена к одному уравнению второго порядка. После того, как из этого уравнения будет найдено y, следует найти z, пользуясь равенством .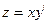

2.При решении системы уравнений путем исключения неизвестных обычно получается уравнение более высокого порядка, поэтому во многих случаях удобнее решать систему путем отыскания интегрируемых комбинаций.

Продолжение 27б

Пример:Решить систему

Решение:

Решим данную систему методом Эйлера. Запишем определитель для нахождения характеристического

уравнения: 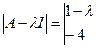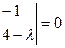, (поскольку система однородная, то для того, чтобы она имела не тривиальное решение, надо, чтобы этот определитель был равен нулю). Получаем харак-кое уравнение и находим его корни: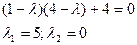

Общее решение имеет вид: ;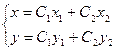

1)

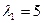
- собственный вектор.

Записываем решение для : ;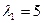

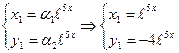2)

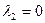
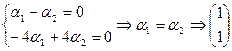- собственный вектор.

Записываем решение для : ;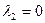

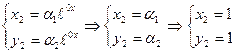Получаем общее решение: .

Выполним проверку:

найдем : 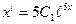и подставляем в первое уравнение данной системы, т.е. .

Получаем: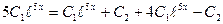

- верное равенство.

Линейные диф. уравнения n-го порядка. Теорема об общем решении неоднородного линейного уравнения n-го порядка.

Линейным диф.уравнением n-го порядка наз-ся уравнение вида: 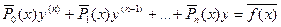(1)

Если в этом ур-ии коэф-т , то, поделив на него, мы приходим к уравнению: (2).

Обычно рассматриваются уравнения типа (2).Предположим, что в ур-и (2)все коэф-ты , а также f(x) непрерывны на некотором промежутке (a,b). Тогда согласно ТСиЕ уравнение (2)имеет единственное решение, удовлетворяющее начальным условиям: 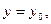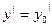, , …, при 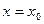. Здесь - любая точка из промежутка (a,b), а все - любые заданные числа. Уравнение (2)удовлетворяет ТСиЕ,поэтому не имеет особых решений.

Опр.: особыми точками являются те, в которых =0.

Свойства линейного уравнения:

1. Линейное уравнение остается таковым при любой замене независимой переменной.
2. Линейное уравнение остается таковым при любой линейной замене искомой функции.

Опр.:если в уравнение (2)положить f(x)=0, то получится уравнение вида: 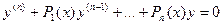(3), которое наз-ся однородным уравнением относительно неоднородного уравнения (2).

Введем в рассмотрение линейный диф-й оператор: (4).С помощью этого оператора можно переписать в краткой форме уравнения (2)и(3):L(y)=f(x), L(y)=0. Оператор (4)обладает следующими простыми свойствами:

1. L(ky)=kL(y);
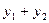2. L( )=L( )+L( )

Из этих двух свойств можно вывести следствие: .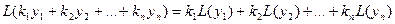

Функция y=y(x) является решением неоднородного уравнения (2),если L(y(x))=f(x), тогда f(x) наз-ся решением уравнения. Значит решением уравнения (3) наз-ся функция y(x), если L(y(x))=0 на рассмотренных промежутках.

Рассм. неоднородное линейное уравнение: , L(y)=f(x).

Будем считать, что все , а также f(x) – непрерывны на (а,b).

Предположим, что мы нашли каким-либо способом частное решение , тогда .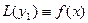

Введем новую неизвестную функцию z по формул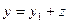е: , где - частное решение.

Подставим её в уравнение: , раскрываем скобки и получаем: .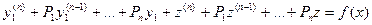

Полученное уравнение можно переписать в виде: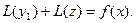

Поскольку - частное решение исходного уравнения, то 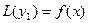, тогда .

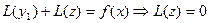Таким образом, мы получили однородное уравнение относительно z. Общим решением этого однородного уравнения является линейная комбинация: , где функции 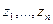- составляют фундаментальную систему решений однородного уравнения. Подставляя z в формулу замены, мы получим: (*) для функции y – неизвестная функция исходного уравнения. Все решения исходного уравнения будут содержаться в (*).

Таким образом, общее решение неоднородного лин. уравнения представляется в виде суммы общего решения однородного линейного уравнения и какого-нибудь частного решения неоднородного уравнения.

(продолжение на той стороне)

30. Теорема существования и единственности решения диф. уравнения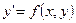

Теорема:Если в уравнении 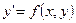правая часть непрерывна в прямоугольнике 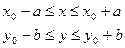и ограничена, а также удовлетворяет условию Липшица: 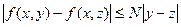, N=const, то существует единственное решение 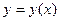, удовлетворяющее начальным условиям и определенное на отрезк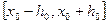е , где .

Доказательство:

Рассмотрим полное метрическое пространство С,точками которого являются всевозможные непрерывные функции y(x), определенные на отрезке 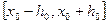, графики которых лежат внутри прямоугольника, а расстояние определяется равенством: 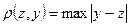. Это пространство часто используется в мат.анализе и называется пространством равномерной сходимости, поскольку сходимость по метрике этого пространства является равномерной.

Заменим диф. уравнение с данными начальными условиями на равносильное ему интегральное уравнение: и рассмотрим оператор А(y), равный правой части этого уравнения: . Этот оператор ставит в соответствие каждой непрерывной функции y функцию А(y), которая также непрерывна и не выходит за пределы прямоугольника, т.к. выполняется следующее неравенство: , тогда оператор Аудовлетворяет 1-му условию принципа сжимающих отображений, т.е. переводит всякую функцию пространства Св функцию из этого же пространства. Исходное уравнение можно записать так: y=A(y)и для доказательства теоремы требуется доказать, что выполняется 2-е условие принципа сжимающих отображений (т.е. сближает точки – условие сжатия), т.е. 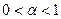. Запишем расстояние между A(y) и A(z), т.е. 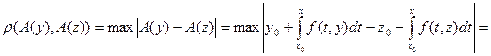( по построению оператора) = .

Пользуясь неравенством Липшица, мы можем записать, что расстояние 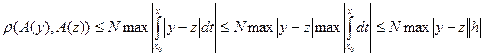. Теперь выберем такое , для которого выполнялось бы следующее неравенство: .

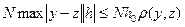следует выбрать так, что 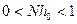, тогда 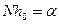. Таким образом мы показали, что .

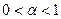Согласно принципу сжимающих отображений существует единственная точка или, что то же самое, единственная функция – решение диф.уравнения, удовлетворяющее заданным начальным условиям.