Методы одномерной оптимизации. Метод «золотого сечения»
В некоторых задачах вычисление значений производной функции представляет существенную трудность, например, когда аналитическое выражение функции неизвестно. В этих случаях рекомендуется применять численные методы, не использующие производных.
Рассмотрим задачу по отысканию экстремума функции одной переменной. Поиск экстремума разделен на два этапа. На первом из них выделяют интервалы значений аргумента 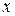 , в которых существует единственная точка экстремума
, в которых существует единственная точка экстремума 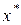 . Этот этап не поддается строгой алгоритмизации и здесь могут быть рекомендованы графический метод, методы подгонки или анализа упрощенной модели. На втором этапе осуществляется уточнение местоположения экстремума.
. Этот этап не поддается строгой алгоритмизации и здесь могут быть рекомендованы графический метод, методы подгонки или анализа упрощенной модели. На втором этапе осуществляется уточнение местоположения экстремума.
Предположим, отыскивается минимум функции 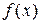 , расположенный на интервале
, расположенный на интервале  . В методе дихотомии при уточнении положения минимума пользуются следующей стратегией. Вычисляют значения функции в двух точках:
. В методе дихотомии при уточнении положения минимума пользуются следующей стратегией. Вычисляют значения функции в двух точках:
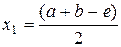 ,
,  ,
,
где е - малая величина, например, требуемая точность нахождения точки экстремума. Пусть оказалось, что 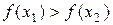 . Тогда точка минимума лежит на интервале
. Тогда точка минимума лежит на интервале  . Если же
. Если же  , то - на интервале
, то - на интервале  . Далее изложенный вычислительный алгоритм повторяется для найденного интервала расположения корня и так до тех пор, пока ширина интервала станет меньше
. Далее изложенный вычислительный алгоритм повторяется для найденного интервала расположения корня и так до тех пор, пока ширина интервала станет меньше  . Решением задачи будет середина заключительного интервала.
. Решением задачи будет середина заключительного интервала.
Более экономичным является метод золотого сечения. В основе этого метода лежит понятие «золотого сечения», введенного Леонардо да Винчи и используемого, в частности, при построении архитектурных сооружений античности и эпохи Возрождения.
В данном методе значения функции вычисляются в точке  , делящей интервал
, делящей интервал  в отношении
в отношении  , и в точке
, и в точке 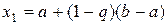 , симметричной точке
, симметричной точке 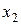 относительно середины интервала. При
относительно середины интервала. При 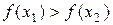 будет
будет  , если же
, если же  , то
, то 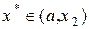 , где
, где 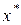 - минимум функции
- минимум функции 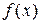 . Предположим оказалось, что
. Предположим оказалось, что 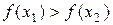 и
и  . Тогда, на второй итерации следует вычислять значения функции в точках
. Тогда, на второй итерации следует вычислять значения функции в точках

Выберем такое  , чтобы
, чтобы 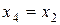 , следовательно
, следовательно  , откуда
, откуда 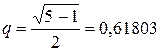 .
.
Деление отрезка в отношении  называют золотым сечением. Это дано название методу. Достоинство метода «золотого сечения» состоит в том, что на второй и последующих итерациях требуется вычисление только одного значения функции.
называют золотым сечением. Это дано название методу. Достоинство метода «золотого сечения» состоит в том, что на второй и последующих итерациях требуется вычисление только одного значения функции.
После каждой итерации происходит сужение интервала неопределенности расположения минимума в  раз. Вычисления прекращаются, когда ширина интервала станет меньше
раз. Вычисления прекращаются, когда ширина интервала станет меньше  . Решением задачи считают середину интервала.
. Решением задачи считают середину интервала.
Пример. Найти минимум функции  методом «золотого сечения» с погрешностью до
методом «золотого сечения» с погрешностью до  .
.
Локализуем минимум. С этой целью определим нули функции из уравнения 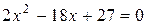 , решая которое находим
, решая которое находим 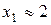 ,
, 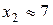 . Минимум функции обязательно расположен между ее нулями. Дальнейшее уточнение минимума осуществим, составив таблицу значений функции с шагом 0,5.
. Минимум функции обязательно расположен между ее нулями. Дальнейшее уточнение минимума осуществим, составив таблицу значений функции с шагом 0,5.
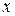 | 2 | 2,5 | 3,5 | ||
 | -2,390 | -3,31 | -3,581 | -3,426 |
Заполнение таблицы прекращается после того, как происходит изменение поведения функции. До  значения функции убывают, а затем начинают возрастать. Это значит, что экстремум функции расположен в окрестности этой точки. Принимаем
значения функции убывают, а затем начинают возрастать. Это значит, что экстремум функции расположен в окрестности этой точки. Принимаем 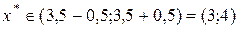 .
.
Уточняем расположение минимума, пользуясь методом золотого сечения. Вычисляем 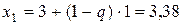 ,
,  ,
, 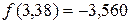 ,
, 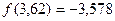 .
.
Имеем 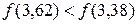 , следовательно
, следовательно  .
.
Вычисляем  и
и 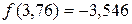 . Так как
. Так как  , то
, то  . Вследствие того, что ширина интервала
. Вследствие того, что ширина интервала 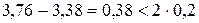 , процесс вычислений прекращаем и принимаем
, процесс вычислений прекращаем и принимаем
 .
.
