Элементарные преобразования матрицы

Определение. Элементарными преобразованиями строк матрицы А называются преобразования следующих трех типов:

1) перестановка двух строк;

2) умножение элементов какой-либо строки на одно и то же число, отличное от нуля;

3) прибавление к элементам одной строки матрицы соответствующих элементов другой строки, умноженных на число, отличное от нуля;

Аналогично определяются элементарные преобразования столбцов матрицы.

Определение. Матрица вида

называется ступенчатой.

Определение . Матрица В называется эквивалентной матрице А, если она получена из матрицы А путем конечного числа элементарных преобразований матрицы А. При этом пишут А ~ В.

Т е о р е м а 1.1. Любую матрицу можно привести к ступенчатой матрице при помощи конечного числа элементарных преобразований строк.

Обратная матрица. Матричные уравнения.

Определение. Обратной матрицей для квадратной матрицы А называется такая матрица А^-1, которая при умножении как слева, так и справа на матрицу А, дает в произведении единичную матрицу Е

А∙А^{– 1} = А^{– 1}∙А = Е.

Определение. Квадратная матрица называется невырожденной, если ее определитель не равен нулю. В противном случае матрица называется вырожденной.

Т е о р е м а 1.2. Для того чтобы матрица была обратимой необходимо и достаточно, чтобы она была невырожденной.

Свойства обратной матрицы:

1. .

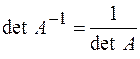2. (A∙B)^{– 1} = B^{– 1}∙A^{– 1}.

3. .

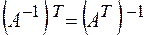Обратная матрица вычисляется по формуле:

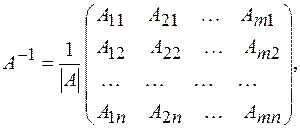(1.1)

где А_ij – алгебраические дополнения элементов а_ij данной матрицы, |А| – определитель матрицы А, причем |А| ¹ 0.

Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом

А∙Х = В (1.2)

Х∙А = В (1.3)

В этих уравнениях А, В, Х – матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров.

Если в уравнениях (1.2) и (1.3) матрица А невырожденная, то их решения соответственно записываются следующим образом:

Х = А^{– 1}∙В.

Х = В∙А^{– 1}.

1.6. Системы линейных алгебраических уравнений(СЛАУ)

Определение. Системы уравнений, содержащие неизвестные только в первой степени называются линейными.

Рассмотрим систему уравнений, у которой число уравнений равно числу неизвестных

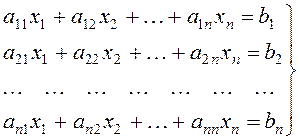, (1.4)

где х₁, х₂, …, х_п – неизвестные, а₁₁, а₁₂, …, а_пп – коэффициенты (заданные числа), b₁, b₂, …, b_n – свободные члены (заданные числа).

Если в (1.4) все свободные члены равны нулю, то система, имеющая вид

, (1.5)

называется однородной.

Система (1.4), в которой хотя бы один из свободных членов не равен нулю, называется неоднородной.

Решение систем линейных алгебраических уравнений

По формулам Крамера

Введем следующие обозначения:

, ,

, …,

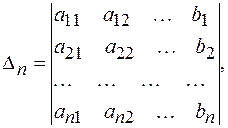
где ∆ – главный определитель системы (1.4), ∆₁, ∆₂, ∆₃, …, ∆_п – дополнительные определители, которые получаются из ∆ путем замены столбцом свободных членов элементов соответственно первого, второго, …, п – го столбцов.

Тогда формулы Крамера запишутся в виде

(1.6)

Т е о р е м а 1. 3. (о решении неоднородной системы).

Если:

а) главный определитель системы (1.4) ∆ ¹ 0, то она имеет единственное решение;

б) ∆ = 0 и все дополнительные определители равны нулю, то система (1.4) имеет бесчисленное множество решений.

в) ∆ = 0 и хотя бы один из дополнительных определителей не равен нулю, то система (1.4) решений не имеет и называется несовместной.

Т е о р е м а 1.4. (о решении однородной системы)

Если:

а) главный определитель однородной системы (1.5) не равен нулю, то эта система имеет единственное решение

х₁ = х₂ = … = х_п = 0

называемое тривиальным;

б) определитель однородной системы равен нулю, то эта система имеет бесчисленное множество нетривиальных решений.

Замечание. Теоремы 1.3, 1.4 играют очень важную роль, как в различных разделах математики, так и во многих практических приложениях.