Краткие теоретические сведения. В соответствии с принципом суперпозиции ток в любой ветви сложной линейной цепи равен алгебраической сумме частичных токов
В соответствии с принципом суперпозиции ток в любой ветви сложной линейной цепи равен алгебраической сумме частичных токов, вызываемых в этой ветви каждым источником ЭДС в отдельности. Аналитическое доказательство этого принципа осуществляется на базе метода контурных токов, по которому
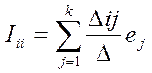 , (4.1)
, (4.1)
где Ii – ток в i-й ветви;
к – число ветвей, содержащих ЭДС;
 – коэффициент пропорциональности (взаимная проводимость между ветвями i и j, где включен источник ej).
– коэффициент пропорциональности (взаимная проводимость между ветвями i и j, где включен источник ej).
Аналитически, пользуясь этим методом расчета, находят составляющие полного тока, вызванные каждой ЭДC в отдельности. Для этого исключают все ЭДС, кроме одной, оставляя внутренние сопротивления реальных источников. Проводят расчет токов с этой ЭДС. Затем исключают все источники, кроме второго, и т.д. Реальный ток определяется как алгебраическая сумма частичных токов.
Методом эквивалентного генератора, называемого еще методом холостого хода и короткого замыкания, определяют ток в какой-то одной ветви. В этом методе интересующая нас ветвь представляется нагрузкой для эквивалентного источника, которым заменяется вся остальная часть цепи с выходными зажимами «ав» (рис.18), совпадающими с началом и концом ветви, где требуется определить ток.
Для эквивалентной схемы замещения (рис. 18) ток в ветви «ав»
 . (4.2)
. (4.2)
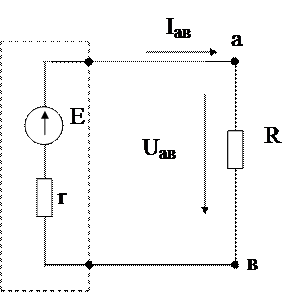 |
Рисунок 18 – Схема замещения электрической цепи для расчета
или исследования методом эквивалентного генератора
Здесь Uaвхх = E – ЭДC эквивалентного генератор; r – внутреннее сопротивление эквивалентного генератора, оно является входным сопротивлением цепи относительно ветви "ав".
При аналитическом расчете этим методом нужно:
1) разомкнуть ветвь "ав" и любым известным методом определить напряжение Uaвхх при Iaв = 0;
2) исключить из оставшейся части цепи все источники ЭДC, оставляя их внутренние сопротивления (если они есть), и вычислить входное сопротивление двухполюсника относительно зажимов "ав" Rвхав. Это и будет внутренним сопротивлением эквивалентного генератора. Используя соотношение (3.1), определить ток в ветви "ав".
Еще можно определить ЭДC эквивалентного генератора и его внутреннее сопротивление экспериментально. Для этого необходимо разорвать ветвь "ав" и измерить напряжение Uaвхх вольтметром, имеющим большое внутреннее сопротивление. Эта величина и будет считаться ЭДС эквивалентного генератора E = Uaвхх. Затем замкнуть накоротко ветвь "ав" и измерить в ней ток короткого замыкания. Внутреннее сопротивление r определяют из соотношения
r = 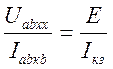 . (4.3)
. (4.3)
Этими двумя опытами и объясняется второе название метода эквивалентного генератора.
