Коэффициенты эластичности для ряда математических функций
Работа № 1
В первой работе рассматривается парнаялинейнаярегрессия:
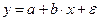(1)
Построение уравнения регрессии сводится к оценке его параметров. Для оценки параметров регрессий, линейных по параметрам, используется метод наименьших квадратов (МНК). Длялинейного уравнениястроится следующая система уравнений относительно параметров а и b:
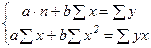
Его решение имеет вид:
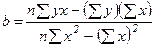или 
, 
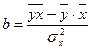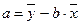, (2)
где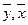 
- средние значения результативного признака у и фактора х, s2х – дисперсия фактора х, п - объем выборки.
Тесноту связи между переменными в линейной регрессии оценивает линейный коэффициент парной корреляции:
, 
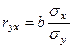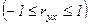(3)
Коэффициент детерминации R2 определяется как квадрат показателя корреляции (линейного коэффициента) и имеет смысл доли факторного среднего квадратического отклонения (СКО) в общем СКО:
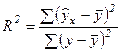(4)
здесь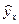 
- значение результативного признака, рассчитанное по уравнению регрессии при подстановке в него заданных значений х.
R2 характеризует качество подгонки кривой под измеренные значения у и изменяется от 0 до 1. В пределе при R2=1 уравнение регрессии точно аппроксимирует заданные значения, т.е. все точки на графике точно ложатся на регрессионную кривую, остаточное СКО равно нулю. Другое предельное значение, R2=0, означает, что уравнение регрессии ничего не дает по сравнению с тривиальным предсказанием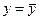 
, и остаточное СКО равно общему; при этом факторное СКО равно нулю. Однако обычные значения R2 находятся между нулем и единицей. Для констатации хорошего качества подготовки кривой нужно, чтобы значение R2было не меньше 0,8. Ошибка аппроксимации для каждого измеренного значения у определяется как относительная (выраженная в процентах) разность между значением у и значением 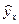, полученным по уравнению регрессии:
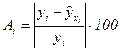(5)
Осреднение этой величины по всем измеренным значениям у дает среднюю ошибку аппроксимации:
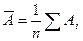(6)
Таким образом, эта величина характеризует среднее отклонение расчетных значений от фактических. Она должна составлять не более 8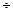 
10%. Большее значение свидетельствует о плохом качестве аппроксимации.
По уравнению регрессии можно определить значение коэффициента эластичности. Для линейного уравнения этот коэффициент рассчитывается следующим образом:
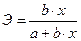(7)
Средний коэффициент эластичности получается при подстановке в формулу среднего значения фактора x.
Статистическая надежность уравнения регрессии в целом оценивается с помощью F- критерия Фишера:
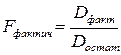(8)
В числителе и в знаменателе этого выражения стоят значения СКО на одну степень свободы (т.е. дисперсии на одну степень свободы). Факторная дисперсия имеет одну степень свободы и не отличается от значения факторной СКО:
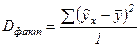(9)
Остаточная дисперсия имеет число степеней свободы, равное (n-2):
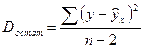(10)
При анализе достоверности уравнения регрессии в целом фактическое значение F-критерия сравнивается с табличным, которое берется при некотором уровне значимости (например, 0,05) и двух степенях свободы - числителя, равной 1, и знаменателя, равной (n - 2):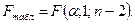 
(см. Таблица F-критерия Фишера)
Далее выдвигается нулевая гипотеза Но том, что остаточная дисперсия равна факторной, т.е.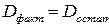 
. Это эквивалентно утверждению статистической незначимости уравнения регрессии. Альтернативная гипотеза Н1 говорит о том, что факторная дисперсия превосходит остаточную, что и означает обоснованность предложенного уравнения и статистическую значимость связи между у и х.
Если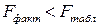 
, Но не отвергается (т.е. принимается), и уравнение регрессии считается статистически незначимым. В противном случае, т.е. 
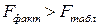превышение факторной дисперсии над остаточной считается неслучайным, и Но отвергается. При этом принимается H1, уравнение регрессии признается статистически значимым.
Прогнозное значение результативного признака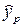 
получается при подстановке в уравнение регрессии прогнозного значения фактора 
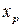. Доверительный интервал прогноза значения 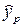для вероятности 
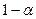определяется по выражению:
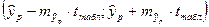(11)
Значение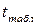 
определяется по таблице t-распределения Стьюдента 
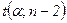при уровне значимости 
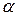и числе степеней свободы 
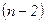. Стандартная ошибка прогноза определяется по формуле:
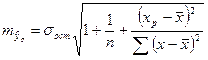(12)
где 
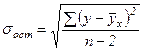(13)
Решение типового задания 1.
По семи территориям Уральского районаза 1995г. известны значения двух признаков:
| Район | Расходы на покупку продовольственных товаров в общих расходах, % (у) | Среднедневная заработная плата одного работающего, руб., (х) |
| Удмуртская республика | 68,8 | 45,1 |
| Свердловская обл | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
1. Рассчитать параметры парной линейной регрессии.
2. Оценить тесноту связи с помощью показателей корреляции и детерминации.
3. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
4. Оценить с помощью средней ошибки аппроксимации качество уравнений.
5. Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования.
6. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости 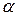=0,05.
Решение.
1. Для расчета параметров а и b линейной регрессии у = а + bх решаем систему нормальных уравнений относительно а и b:
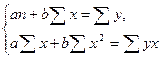
По исходным данным рассчитываем значение всех сумм:
| N п/п | y | x | ух | x2 | y2 |  |  |  |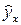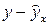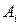
| 68,8 | 45,1 | 3102,88 | 2034,01 | 4733,44 | 61,3 | 7,5 | 10,9 | |
| 61,2 | 59,0 | 3610,80 | 3481,00 | 3745,44 | 56,5 | 4,7 | 7,7 | |
| 59,9 | 57,2 | 3426,28 | 3271,84 | 3588,01 | 57,1 | 2.8 | 4,7 | |
| 56,7 | 61,8 | 3504,06 | 3819,24 | 3214,89 | 55,5 | 1,2 | 2,1 | |
| 55,0 | 58,8 | 3234,00 | 3457,44 | 3025,00 | 56,5 | -1,5 | 2,7 | |
| 54,3 | 47,2 | 2562,96 | 2227,84 | 2948,49 | 60,5 | -6,2 | 11,4 | |
| 49,3 | 55,2 | 2121,36 | 3047,04 | 2430,49 | 57,8 | -8,5 | 17,2 | |
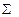 | 405,2 | 384,3 | 22162,34 | 21338,41 | 23685,76 | 405,2 | 0,0 | 56,7 |
Определяем значение параметра b
= 
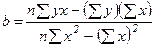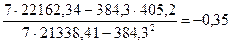
Среднее значение переменных
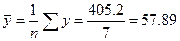(14)
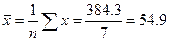(15)
С их помощью определим параметр а: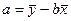 
= 57,89 + 0,35 × 54,9 = 77,11
Получаем уравнение линейной регрессии: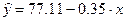 
С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 процентных пункта.
Линейный коэффициент парной корреляции: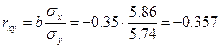 
Здесь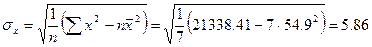 
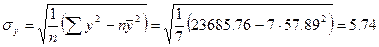
Cвязь умеренная обратная.
Коэффициент детерминации рассчитывается как квадрат коэффициента корреляции:
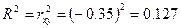
Вариация результата на 12,7% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения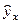 
(колонка 7), а также разности между измеренными значениями и рассчитанными (колонка 8). Величины ошибок аппроксимации в колонке 9 рассчитаем как абсолютную величину значений в колонке 8 по отношению к измеренным значениям в колонке 2 в процентах: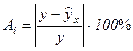 
Найдем величину средней ошибки аппроксимации: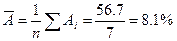 
В среднем расчетные значения отклоняются от фактических на 8,1%
Рассчитаем средний коэффициент эластичности линейной регрессии:
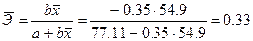
В среднем при увеличении х на 1% значение у уменьшается на 0.33%
Рассчитаем значение F-критерия: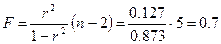 
Поскольку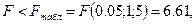 
гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения следует принять.
Теперь рассчитаем прогнозное значение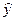 
по линейной модели при прогнозном значении фактора 
.
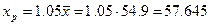Прогноз результата: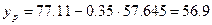 
.
Определим доверительный интервал для этого прогноза. Для этого нам надо рассчитать стандартную ошибку прогноза по формуле:
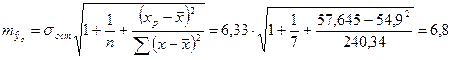
Здесь: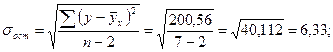 
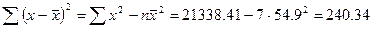
Доверительный интервал рассчитывается так: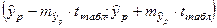 
Здесь: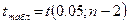 
(берем двухстороннее значение t-критерия Стьюдента): t(0,05;5)=2,57
Доверительный интервал равен: (39,42;74,38). Истинное значение прогноза с вероятностью 0,95 попадает в этот интервал.
Работа № 2
Во второй работе рассматривается парная нелинейная регрессия. Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
- полиномы разных степеней у = а + b1 х + b2 х2 + b3 х3 + e;
- равносторонняя гипербола у = а+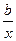 
+ e.
Регрессии, нелинейные по оцениваемым параметрам:
- степенная у = а∙ хb∙ e;
- показательная у = а ∙ bх ∙ e;
- экспоненциальная у = еа+bх ∙ e.
Построение уравнения регрессии сводится к оценке его параметров. Для оценки параметров регрессий используется метод наименьших квадратов (МНК). Перед использованием МНК необходимо произвести линеаризацию (с помощью преобразований нелинейную связь переводится в линейную) нелинейной регрессии.
Дляпреобразованноголинейного уравнениястроится следующая система уравнений относительно параметров а и b:
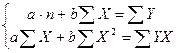
Его решение имеет вид: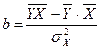 
, 
,
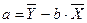где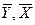 
- средние значения ln у и ln х, s2х – дисперсия ln х, п - объем выборки.
Тесноту связи между переменными в нелинейной регрессии оценивает индекс корреляции (0£ rxy £ 1):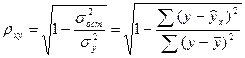 
.
Оценку качества построенной модели даст индекс детерминации – квадрат индекса корреляции - и средняя ошибка аппроксимации.
Остальные показатели рассчитываются также как в линейной регрессии, используя аналогичные формулы (4-6, 8-13).
Средний коэффициент эластичности Э показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения: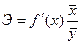 
.
Коэффициенты эластичности для ряда математических функций
| Вид функции, y | Первая производная, 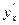 | Коэффициент эластичности,  |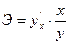
| Линейная y=a+b·x+ε | b |  |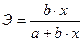
| Парабола второго порядка y=a+b·x+с·x2+ε | B+2·c·x |  |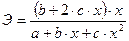
Гипербола  |  |  |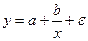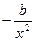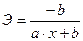
| Показательная y=a·bx·ε | lnb·a·bx | Э=x·lnb |
| Степенная y=a·xb·ε | a·b·xb-1 | Э=b |
| Полулогарифмическая y=a+b·lnx+ε | |  |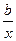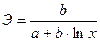
Логистическая  |  |  |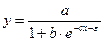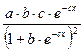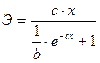
Обратная  |  |  |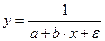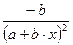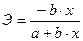
Решение типового задания 2.
По семи территориям Уральского районаза 1995г. известны значения двух признаков:
| Район | Расходы на покупку продовольственных товаров в общих расходах, % (у) | Среднедневная заработная плата одного работающего, руб., (х) |
| Удмуртская республика | 68,8 | 45,1 |
| Свердловская обл | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55.0 | 58,8 |
| Курганская обл | 54,3 | 47,2 |
| Оренбургская обл. | 49.3 | 55,2 |
1. Рассчитать параметры парной степенной регрессии и равносторонней гиперболы..
2. Оценить тесноту связи с помощью показателей корреляции и детерминации.
3. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
4. Оценить с помощью средней ошибки аппроксимации качество уравнений.
5. Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования.
6. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α =0,05.
Решение.
1а. Построению степенной модели у = а ∙ хb предшествует процедура линеаризации переменных. Она производится путем логарифмирования обеих частей уравнения:
lg y = lg a + b∙ lg x;
Y = C + b ∙X,
где Y = lg y, C = lg a, X = lg x.
Для расчетов используем данные:
| Y | X | YX | Y2 | X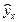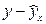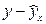2 |  |  | ( )2 | | |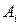
| 1,8376 1,7868 1,7774 1,7536 1,7404 1,7348 1,6928 | 1,6542 1,7709 1,7574 1,7910 1,7694 1,6739 1,7419 | 3,0398 3,1642 3,1236 3,1407 3,0795 2,9039 2,9487 | 3,3768 3,1927 3,1592 3,0751 3,0290 3,0095 2,8656 | 2,7364 3,1361 3,0885 3,2077 3,1308 2,8019 3,0342 | 61,0 56,3 56,8 55,5 56,3 60,2 57,4 | 7,8 4,9 3,1 1,2 -1,3 -5,9 -8,1 | 60,8 9,6 1,4 1,7 34,8 65,6 | 11,3 5,2 2,1 2,4 10,9 16,4 | |
| Итого | 12,3234 | 12,1587 | 21,4003 | 21,7078 | 21,1355 | 403,5 | 1,7 | 197,9 | 56,3 |
| Ср. знач. | 1,7605 | 1,7370 | 3,0572 | 3,1011 | 3,0194 | х | х | 28,27 | 8,0 |
| s | 0,0425 | 0,0484 | х | х | х | х | х | х | х |
| s2 | 0,0018 | 0,0023 | х | х | х | х | х | х | х |
Рассчитаем С и b:
; 
.
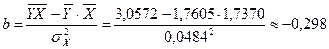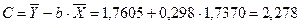Получим линейное уравнение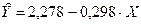 
. Выполнив его потенцирование, получим 
.
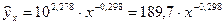Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 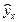. По ним рассчитываем показатели:
- тесноты связи – индекс корреляции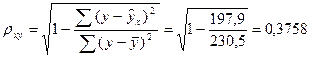 
;
- индекс детерминации R2 = r2xy = 0,1412 ;
- среднюю ошибку аппроксимации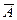 
= 8,0%.
Рассчитаем средний коэффициент эластичности: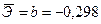 
В среднем при увеличении х на 1% значение у уменьшается на 0,298%
Рассчитаем значение F-критерия: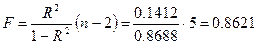 
Поскольку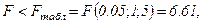 
гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения следует принять.
Теперь рассчитаем прогнозное значение 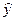по степенной модели при прогнозном значении фактора 
.
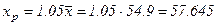Прогноз результата: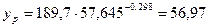 
.
Определим доверительный интервал для этого прогноза. Для этого нам надо рассчитать стандартную ошибку прогноза по формуле:
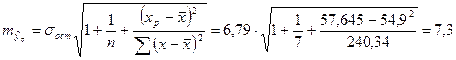
Здесь: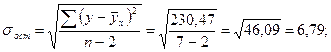 
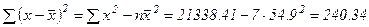
Доверительный интервал рассчитывается так: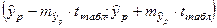
Здесь: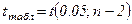 
(берем двухстороннее значение t-критерия Стьюдента): t(0,05;5)= 2,57
Доверительный интервал равен: (38,47;75,64).
Истинное значение прогноза с вероятностью 0,95 попадает в этот интервал.
1б. Уравнение равносторонней гиперболы у = а + 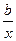линеаризуется при замене z = 
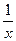, тогда у = а + b ∙ z.
Для расчетов используем данные:
| y | z | уz | z2 | y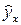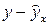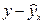2 | | | (  )2 | | |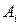
| 68,8 | 0,0222 | 1,5255 | 0,000492 | 4733.44 | 61,8 | 7,0 | 49,0 | 10,2 | |
| 61,2 | 0,0169 | 1,0373 | 0,000287 | 3745,44 | 56,3 | 4,9 | 24,01 | 8,0 | |
| 59,9 | 0,0175 | 1,0472 | 0,000306 | 3588,01 | 56,9 | 3,0 | 9,0 | 5,0 | |
| 56,7 | 0,0162 | 0,9175 | 0,000262 | 3214,89 | 55,5 | 1,2 | 1,44 | 2,1 | |
| 55,0 | 0,0170 | 0,9354 | 0,000289 | 3025,00 | 56,4 | -1,4 | 1,96 | 2,5 | |
| 54,3 | 0,0212 | 1,1504 | 0,000449 | 2948,49 | 60,8 | -6,5 | 42,25 | 12,0 | |
| 49,3 | 0,0181 | 0,8931 | 0,000328 | 2430,49 | 57,5 | -8,2 | 67,24 | 16,6 | |
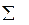 | 405,2 | 0,1291 | 7,5064 | 0,002413 | 23685,76 | 405,2 | 0,0 | 194,9 | 56,5 |
| Среднее значение | 57,9 | 0,0184 | 1,0723 | 0,000345 | 3383,68 | х | х | 27,84 | 8,1 |
| s | 5,74 | 0,002145 | х | х | х | х | х | х | х |
| s2 | 32,9476 | 0,000005 | х | х | х | х | х | х | х |
Значения параметров регрессии а и b составили:
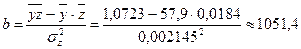
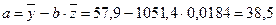
Получено уравнение: 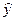= 38,5 +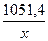 
.
Индекс корреляции: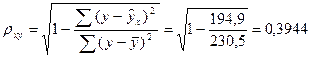 
.
Средняя ошибка аппроксимации 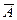= 8,1%.
Рассчитаем средний коэффициент эластичности: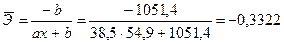 
В среднем при увеличении х на 1% значение у уменьшается на 0,332%
Рассчитаем значение F-критерия: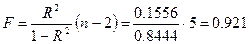 
Поскольку 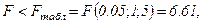гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения следует принять. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.