Розв’язання завдань з теми «Ряди».
Завдання 1.
Довести розбіжність ряду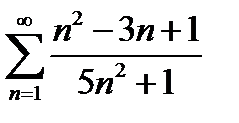 
.
Розв’язання. Перевіримо необхідну умову збіжності ряду, тобто обчислимо
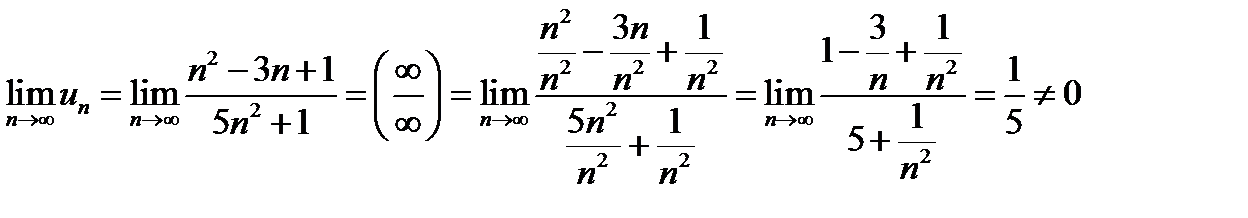. Необхідна умова збіжності ( 
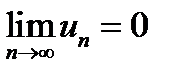) не виконується, тобто ряд розбігається.
Завдання 2.
Перевірити, чи збігаються або розбігаються ряди.
а1)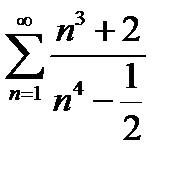 
.
Розв’язання. Порівняємо даний ряд з рядом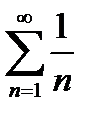 
, який розбігається. Для цього обчислимо
.
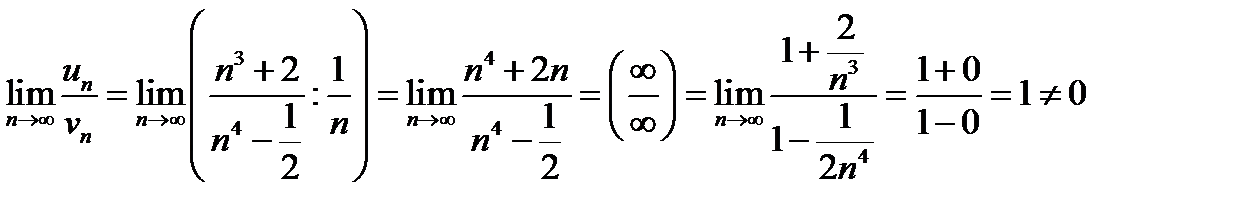Оскільки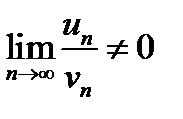 
, то заданий ряд також розбігається згідно граничної ознаки порівняння рядів.
Відповідь. Ряд розбігається.
Зауваження. Якщо загальний член ряду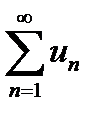 
є дробово-раціональною функцією відносно 
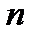, то загальний член ряду для порівняння зручно брати у вигляді 
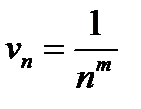, де 
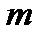- різниця між степенями многочленів знаменника і чисельника у 
.
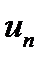а2)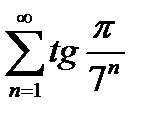 
.
Розв’язання. Порівняємо цей ряд з рядом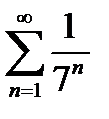 
, який є геометричною прогресією із знаменником 
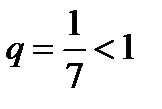і збігається.
.
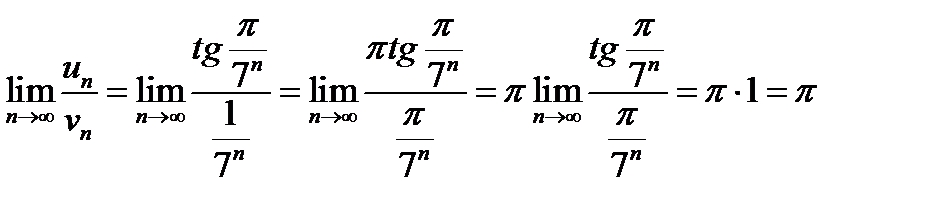Оскільки границя скінченна, то заданий ряд, як і допоміжний, збігається.
Відповідь. Ряд збігається.
б)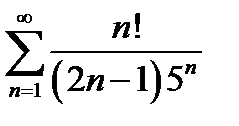 
.
Розв’язання. Для перевірки збіжності або розбіжності цього ряду застосуємо ознаку Даламбера. За умовою маємо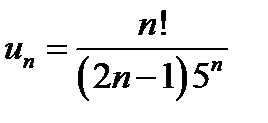 
, тоді 
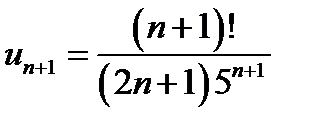. Обчислимо границю відношення 
:
.
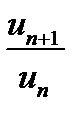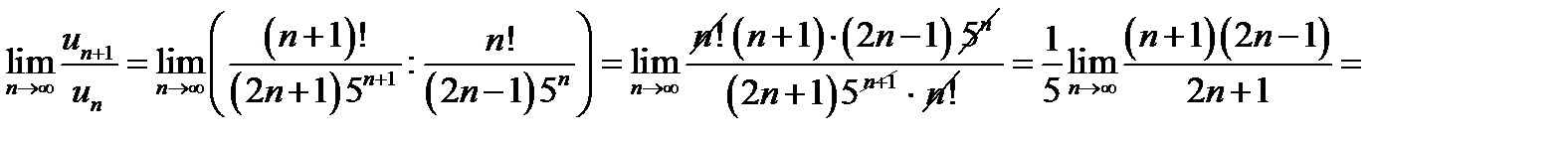
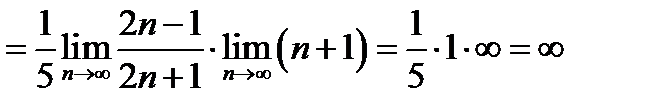За ознакою Даламбера ряд розбігається.
Відповідь. Ряд розбігається.
в)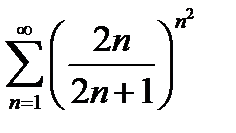 
.
Розв’язання. В цьому випадку зручно скористатися радикальною ознакою Коші:
.
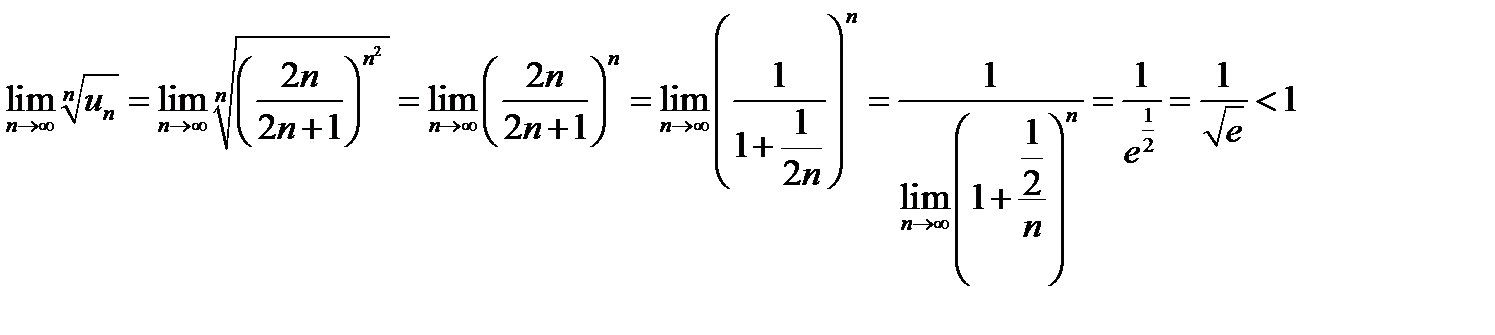Отже, заданий ряд збігається.
Відповідь. Ряд збігається.
г)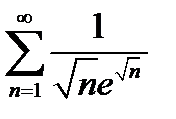 
.
Розв’язання. Оскільки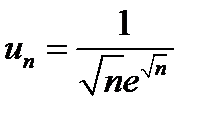 
є значенням функції 
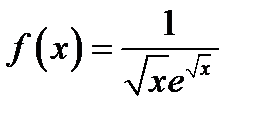при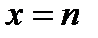 
і ця функція неперервна і монотонно спадає в проміжку 
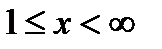, то обчислимо невласний інтеграл
.
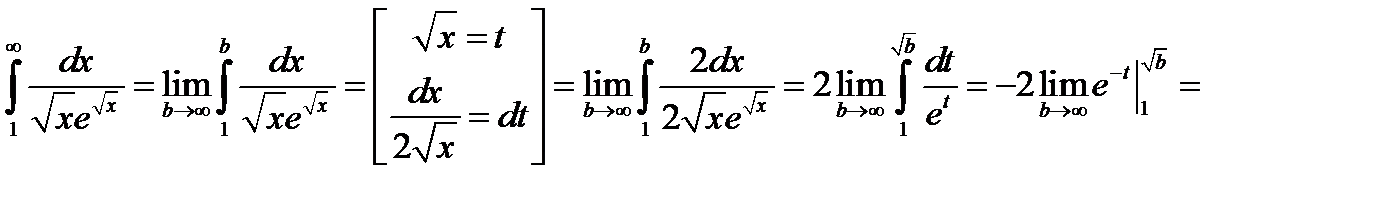
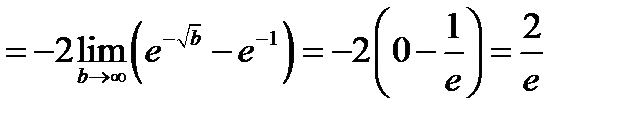Невласний інтеграл збігається, отже, за інтегральною ознакою Коші збігається і заданий ряд.
Відповідь. Ряд збігається.
Завдання 3.
Визначити радіус та інтервал збіжності степеневого ряду.
а)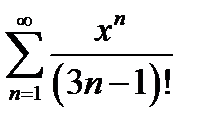 
.
Розв’язання. Знайдемо радіус збіжності за формулою Даламбера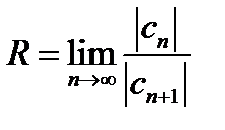 
. За умовою 
, 
.
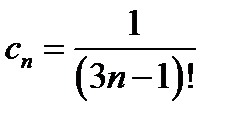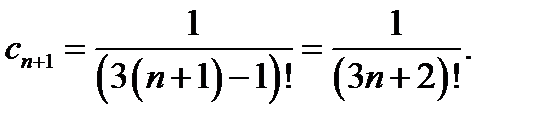
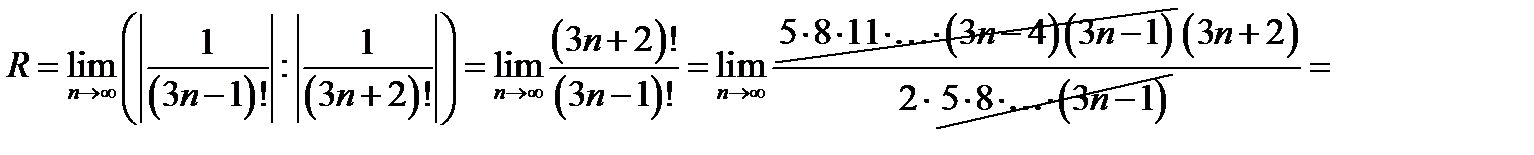
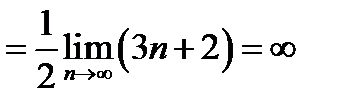Оскільки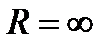 
, то ряд збігається на всій числовій осі.
Відповідь. ,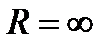 
.
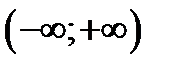б)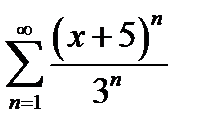 
.
Розв’язання. За ознакою Даламбера ряд збігається, якщо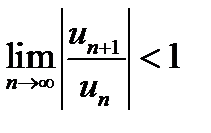 
. За умовою 
, 
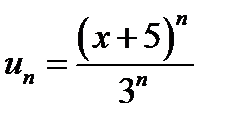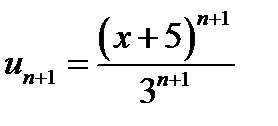. Обчислимо
.
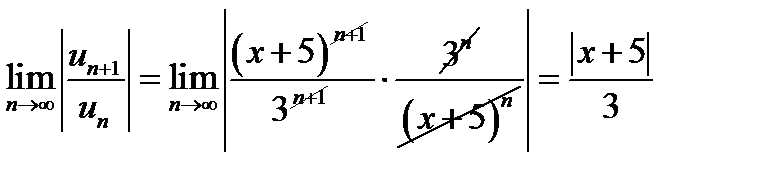Заданий ряд збігається, якщ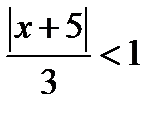о 
або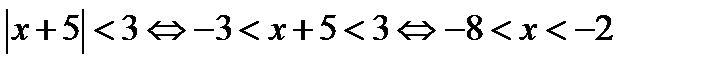 
. Отже, інтервал збіжності 
, 
.
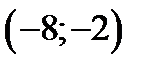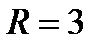Відповідь. , .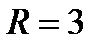
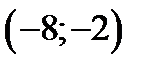Завдання 4.
Розкласти у степеневий ряд функцію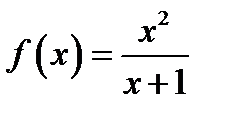 
і визначити його область збіжності.
Розв’язання. Перетворимо задану функцію:
.
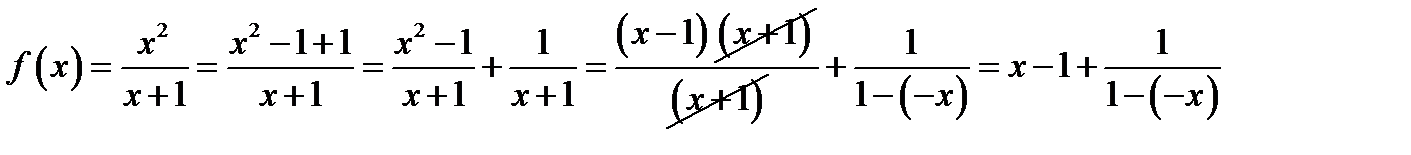Застосуємо формулу: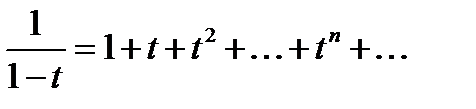 
, 
.
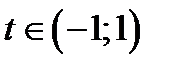Зробимо в цій формулі заміну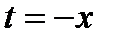 
, отримаємо:
, 
.
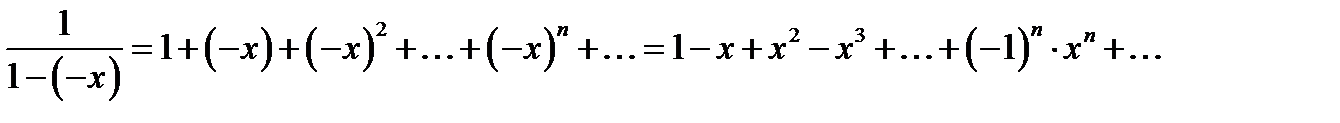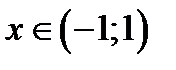Тоді
, .
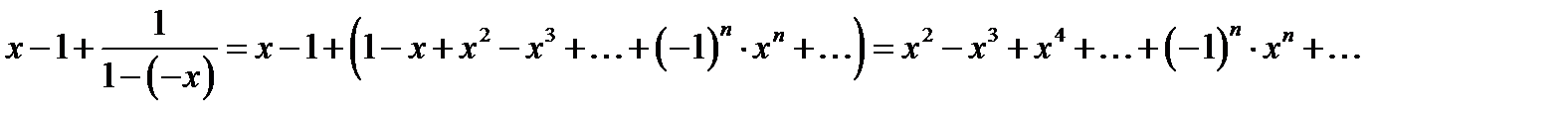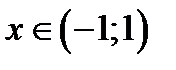Відповідь.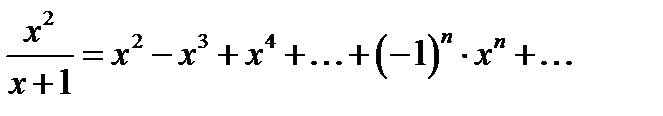 
, область збіжності ряду .
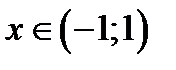Завдання 5.
а) Функцію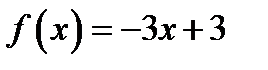 
, що задана на проміжку 
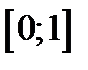, розкласти в ряд Фур’є за синусами.
Розв’язання. Довизначимо задану функцію на проміжку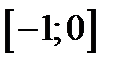 
непарним способом. Тоді її ряд Фур’є буде містити тільки синуси, тобто
,
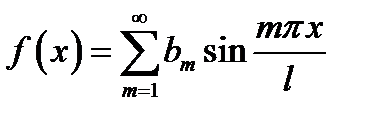де
.
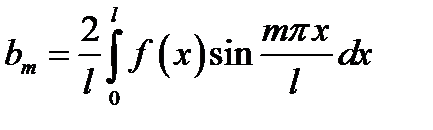За умовою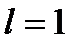 
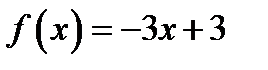, . Тоді
, 
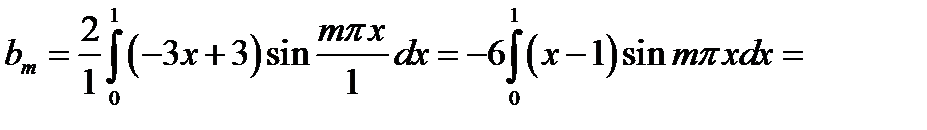
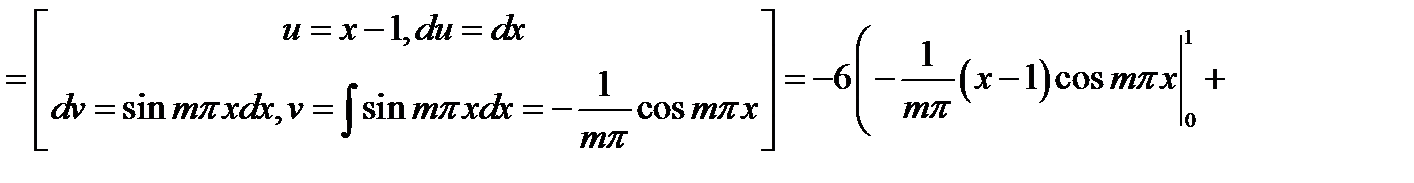
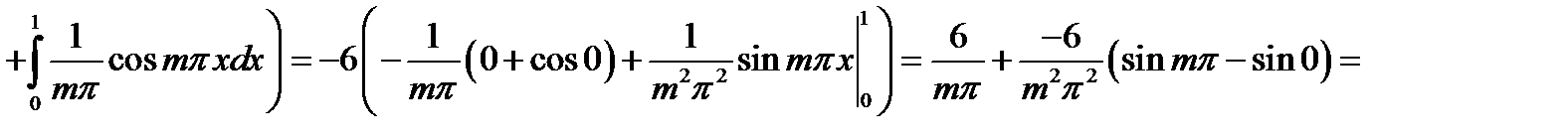
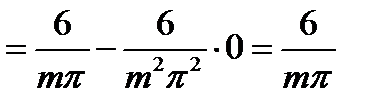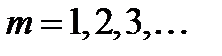
Таким чином,
.
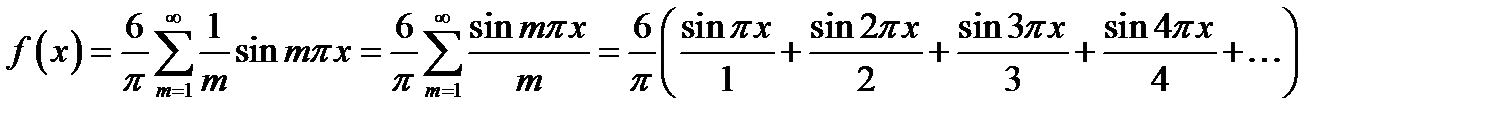Відповідь.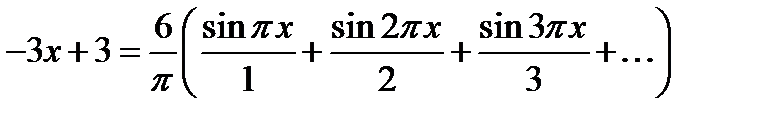 
.
б) Функцію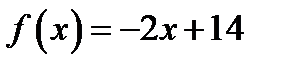 
, що задана на проміжку 
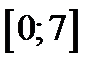, розкласти в ряд Фур’є за косинусами.
Розв’язання. Довизначимо задану функцію на проміжку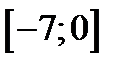 
парним способом. Ряд Фур’є при цьому містить тільки вільний член і косинуси, тобто
,
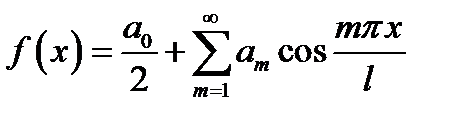де
, 
.
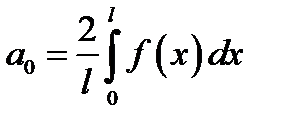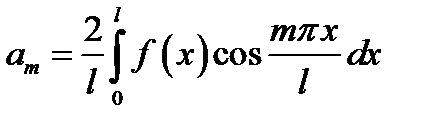За умовою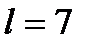 
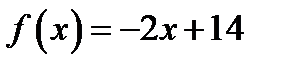, . Тому
.
, 
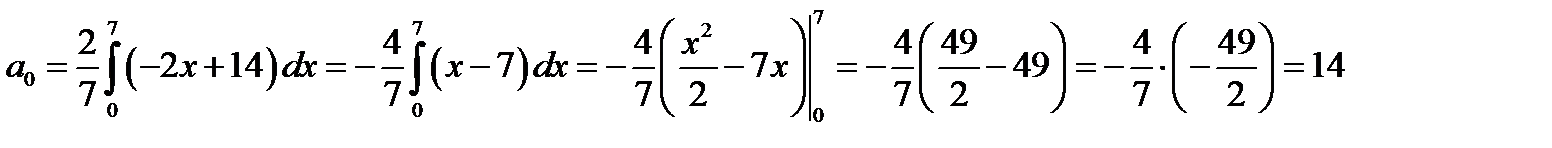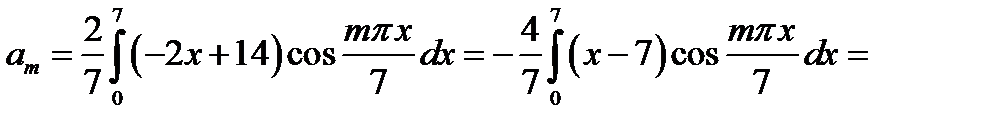
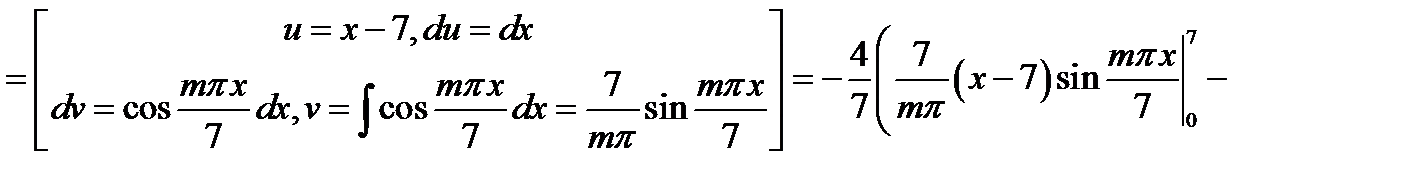
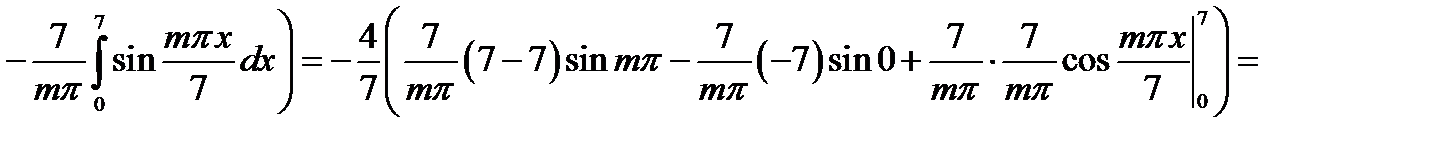
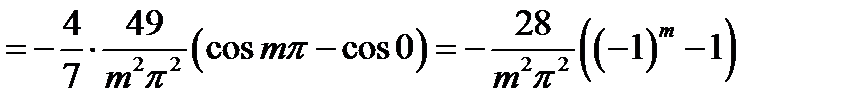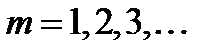
Таким чином,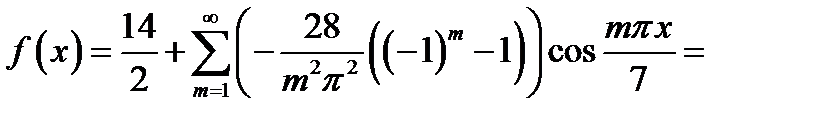 
.
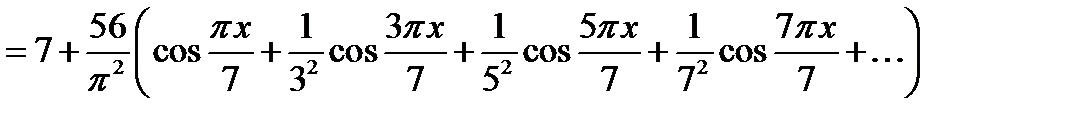Відповідь.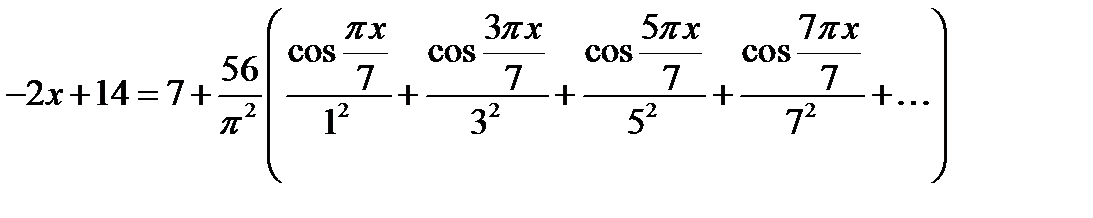 
.
Література
1. Письменный Д.Т. Конспект лекций по высшей математике. Ч.1. – М.: Рольф, 2000.
2. Письменный Д.Т. Конспект лекций по высшей математике. Ч.2. – М.: Рольф, 2000.
3. Дубовик В.П., Юрик І.І. Вища математика. – К.: Видавництво А.С.К., 2003.
4. Беклемешев Д.В. Курс аналитической геометрии и линейной алгебры. – М. Наука, 1984.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1. – М.: Высшая школа, 1986.
6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.2. – М.: Высшая школа, 1986.
7. Герасимчук В.С., Васильченко Г.С., Кравцов В.И. Курс классической математики в примерах и задачах. Ч.1. – Донецк, 2004.
8. Герасимчук В.С., Васильченко Г.С., Кравцов В.И. Курс классической математики в примерах и задачах. Ч.2. – Донецк, 2004.
9. Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1969.
10. Ковалішина І.В. Елементи лінійної алгебри та аналітичної геометрії. – Харків, ХарДАЗТ, 2000.
11. Ковалішина І.В. Диференціальне числення функцій однієї і кількох змінних. – Харків, ХарДАЗТ, 2001.
12. Горбатенко Ж.К. Функції, їх дослідження та побудова графіків. – Донецьк, ДонІЗТ, 2001.
13. Горбатенко Ж.К. Невизначений та визначений інтеграли. – Донецьк, ДонІЗТ, 2000.
14. Горбатенко Ж.К. Диференціальні рівняння. – Донецьк, ДонІЗТ, 2002.