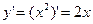Общее определение производной

Лекция 5. Производная. Основные теоремы о производных. Основные формулы дифференцирования функций

Задача о касательной

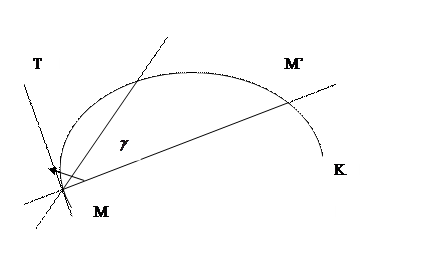
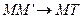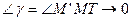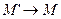Пусть М – фиксированная точка кривой К. MM’ – секущая, проходящая через точки М и М’. Может случиться, что М’ стремится к М, секущая , где МТ – предельное положение, то есть при , тогда предельная прямая МТ называется касательной.

Определение

Касательной к данной непрерывной кривой в данной ее точке М (точка касания) называется предельное положение секущей ММ’, проходящей через точку М, когда вторая точка пересечения М’ неограниченно приближается по кривой к первой.

Если секущая ММ’ при 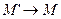не имеет предельного положения, то говорят, что касательной к данной линии в точке М не существует.

Задача

Зная уравнение непрерывной линии y=f(x) найти уравнение касательной в данной точке ее M(x,y), предполагая, что касательная существует.

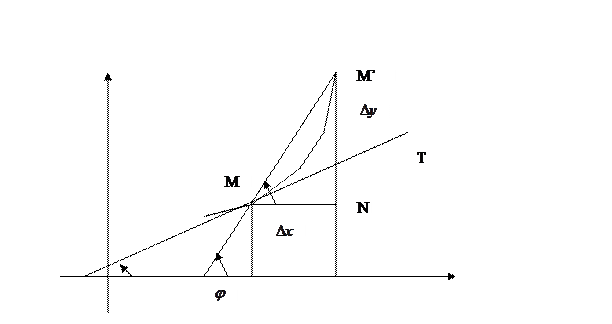
Наряду с точкой M(x,y) возьмем на линии другую точку 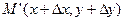. Проведем секущую MM’ и прямые MN||OX,M’N||OY получим прямоугольный треугольник MNM’ с катетам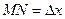и и .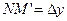

Пусть секущая MM’ составляет с ОХ угол 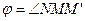. Из 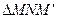определяем угловой коэффициент секущей 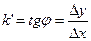(1).

Пусть 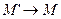, тогда 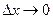и секущая 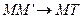(предельное положение секущей). Обозначим через 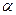угол образованный касательной МТ с положительным направлением оси ОХ. При 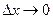, 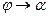. Если касательная МТ не перпендикулярна ОХ, то в силу непрерывности тангенса получим .

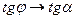Отсюда переходя к пределу при 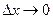в равенстве (1) найдем угловой коэффициент 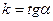касательной МТ.

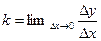(2)

Предел, стоящий в правой части равенства (2), называется производной функции y=f(x) в точке х и сокращенно обозначается следующим образом

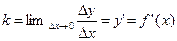(3)

Таким образом, угловой коэффициент касательной к графику функции равен значению ее производной в точке касания.

Зная угловой коэффициент касательной, легко написать ее уравнение.

Обозначим через 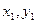коэффициенты точки касания, а x,y – текущие координаты, то уравнение касательной к линии y=f(x) в точке 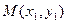имеет вид 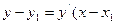), где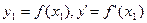

Общее определение производной

Рассмотрим вопрос о производной в общем виде

Предполагаем, что функция y=f(x) определена на некотором конечном или бесконечном интервале 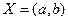и непрерывна на этом интервале. Пусть 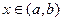- фиксированная точка на этом интервале. Даем х приращение 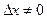такое, что 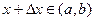. Тогда функция y=f(x) получает соответствующее приращение

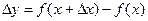(1)

Составим отношение 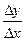(2)

Это отношение показывает во сколько раз на данном промежутке 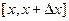приращение функции y больше приращения аргумента х.

Пусть 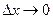. Тогда 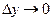в силу непрерывности функции y.

Обозначим 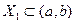- множество точек интервала (a,b) для которых имеет смысл предельный переход 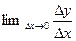(3).

Тогда формула 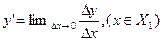(4)

Определяет некоторую функцию y’=f’(x), носящую название производной функции f(x).

Определение

Производной функции y=f(x) называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю. Если этот предел существует.

Функция, имеющая производную на множестве 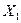называется дифференцируемой на этом множестве.

Если 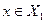фиксировано, то в силу (4) производная y’ представляет собой скорость изменения функции y относительно аргумента х в точке х.

Приняты обозначения:

y’=f’(x) – Лагранж;

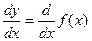- Лейбниц;

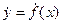- Ньютон.

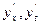- дифференцирование функций по определенному аргументу.

Для значения производной функции y=f(x) в фиксированной точке используются обозначения

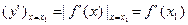- это число.

Используя формулу (1) можно записать

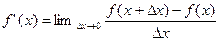(5).

С помощью формулы (5), опираясь на теоремы о пределах можно находить производные функции.

Пример

Найти производную функции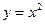

Решение

Х – произвольное фиксированное значение аргумента. Давая 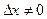имеем

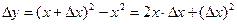и следовательно 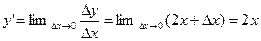, то есть