Производная по направлению
В п. 5.9 были даны определения скалярного поля и способ его геометрического изображения. Выясним, какими характеристиками обладает такое поле.
Рассмотрим трехмерное скалярное поле 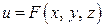 и построим величину, которая характеризует скорость изменения этого поля в некоторой точке
и построим величину, которая характеризует скорость изменения этого поля в некоторой точке 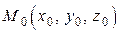 в направлении вектора
в направлении вектора 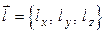 .
.
Пусть функция 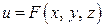 является дифференцируемой в области
является дифференцируемой в области 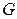 . Проведем из точки
. Проведем из точки 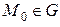 вектор
вектор 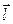 и возьмем на нем какую-нибудь точку
и возьмем на нем какую-нибудь точку 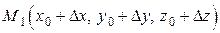 . Построим на отрезке
. Построим на отрезке 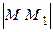 как на диагонали параллелепипед, ребра которого параллельны осям прямоугольной декартовой системы координат (рис. 5.10.1). Угол с осью
как на диагонали параллелепипед, ребра которого параллельны осям прямоугольной декартовой системы координат (рис. 5.10.1). Угол с осью 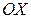 обозначим
обозначим 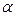 , с осью
, с осью 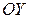 –
– 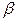 , с осью
, с осью 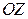 –
– 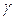 .
.
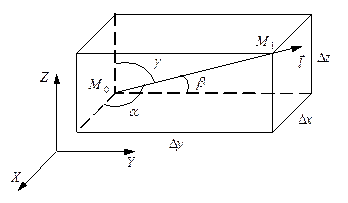
Рис. 5.10.1
Составим разность 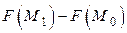 , которая характеризует изменение скалярного поля при переходе из точки
, которая характеризует изменение скалярного поля при переходе из точки 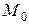 в точку
в точку 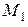 . Эту разность разделим на расстояние между точками
. Эту разность разделим на расстояние между точками 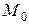 и
и 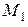 :
: 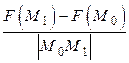 . С точки зрения физики данная величина характеризует среднюю скорость изменения скалярного поля на отрезке
. С точки зрения физики данная величина характеризует среднюю скорость изменения скалярного поля на отрезке 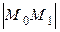 .
.
Устремим теперь точку 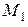 к
к 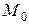 так, чтобы точка
так, чтобы точка 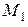 постоянно оставалась на векторе
постоянно оставалась на векторе 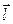 и при этом
и при этом 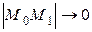 .
.
Определение. Если существует предел отношения приращения скалярного поля 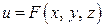 в точке
в точке 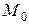 в направлении вектора
в направлении вектора 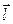 к длине отрезка
к длине отрезка 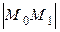 , когда
, когда 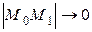 , то этот предел называется производной скалярного поля в точке
, то этот предел называется производной скалярного поля в точке 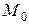 в направлении
в направлении 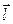 и обозначается:
и обозначается: 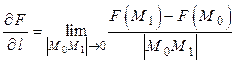 .
.
Очевидно, что производная скалярного поля по направлению 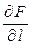 равна скорости изменения скалярного поля
равна скорости изменения скалярного поля 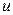 в направлении
в направлении 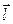 . Если
. Если 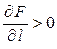 , то поле в данном направлении возрастает, если
, то поле в данном направлении возрастает, если 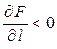 – убывает.
– убывает.
Найдем правило для вычисления производной по направлению. В нашем случае
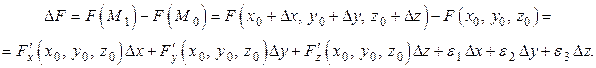
Поскольку три последних слагаемых в полученном выражении бесконечно малые величины, то их сумма также является бесконечно малой величиной 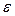 . Кроме того, выразим
. Кроме того, выразим 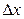 ,
, 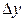 и
и 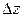 через величину отрезка
через величину отрезка 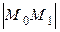 . Таким образом,
. Таким образом,
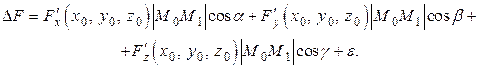 .
.
Разделив полное приращение скалярного поля на длину отрезка 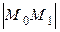 , получим:
, получим:
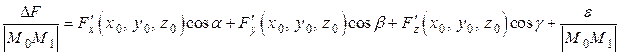 .
.
Перейдем к пределу в полученном выражении:
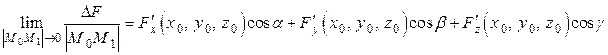 .
.
Итак,
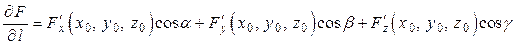 ,
,
то есть для вычисления производной по направлению необходимо знать значения частных производных в точке 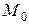 и направляющие косинусы вектора, по направлению которого вычисляется производная.
и направляющие косинусы вектора, по направлению которого вычисляется производная.
В частности, если 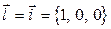 , то
, то 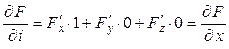 , если
, если 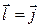 , то
, то 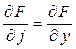 , если
, если 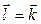 , то
, то 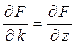 . Следовательно, частные производные функции
. Следовательно, частные производные функции 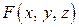 – это производные скалярного поля
– это производные скалярного поля 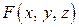 в направлении соответствующих ортов.
в направлении соответствующих ортов.
В плоском случае  .
.
Градиент
Пусть в некоторой трехмерной области  задано скалярное поле
задано скалярное поле  , которое дифференцируемо во всех его точках.
, которое дифференцируемо во всех его точках.
Определение 5.11.1. Градиентом скалярного поля в точке 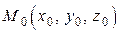 называется вектор
называется вектор 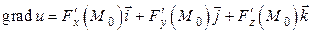 .
.
Из определения 5.11.1 следует, что каждой точке скалярного поля соответствует не только значение функции, но и вполне определенный вектор 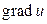 . Между градиентом функции
. Между градиентом функции  в некоторой точке и производной по выбранному направлению в этой же точке существует определенная связь.
в некоторой точке и производной по выбранному направлению в этой же точке существует определенная связь.
Теорема. Проекция градиента скалярного поля 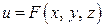 в точке
в точке 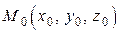 на направление орта
на направление орта 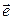 равна производной этого поля в точке
равна производной этого поля в точке 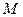 по направлению орта
по направлению орта 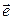 .
.
Доказательство. Как известно, координаты единичного вектора 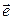 в прямоугольной декартовой системе координат равны направляющим косинусам этого вектора, то есть
в прямоугольной декартовой системе координат равны направляющим косинусам этого вектора, то есть 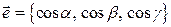 . Найдем проекцию вектора
. Найдем проекцию вектора 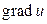 на орт
на орт 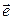 (п. 7):
(п. 7):
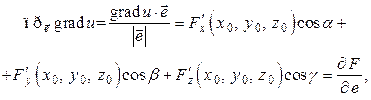
что и требовалось доказать.
Вычислим теперь 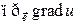 или, что то же самое,
или, что то же самое, 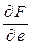 , воспользовавшись другим способом вычисления скалярного произведения:
, воспользовавшись другим способом вычисления скалярного произведения:
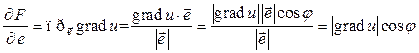 , (5.11.1)
, (5.11.1)
где 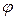 – угол между направлением орта
– угол между направлением орта 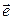 и вектора
и вектора 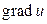 . Анализ выражения (5.11.1) показывает, что наибольшее значение производная по направлению будет иметь тогда, когда
. Анализ выражения (5.11.1) показывает, что наибольшее значение производная по направлению будет иметь тогда, когда 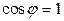 , то есть
, то есть 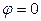 . Таким образом, производная по направлению максимальна, когда это направление совпадает с вектором
. Таким образом, производная по направлению максимальна, когда это направление совпадает с вектором 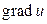 .
.
Определение 5.11.2. 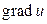 – есть вектор, указывающий направление наибольшего возрастания скалярного поля в данной точке и имеющий модуль, равный скорости этого возрастания.
– есть вектор, указывающий направление наибольшего возрастания скалярного поля в данной точке и имеющий модуль, равный скорости этого возрастания.
Выяснив физический смысл градиента, определим ориентацию вектора 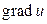 в скалярном поле. Как было сказано в п. 5.9, если скалярное поле имеет вид
в скалярном поле. Как было сказано в п. 5.9, если скалярное поле имеет вид 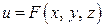 , то его геометрическим образом будет поверхность уровня
, то его геометрическим образом будет поверхность уровня 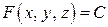 . Нормаль к данной поверхности в точке
. Нормаль к данной поверхности в точке 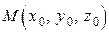 имеет уравнение (п. 5.8):
имеет уравнение (п. 5.8):
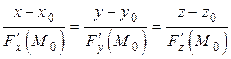 .
.
Направляющий вектор этой нормали равен 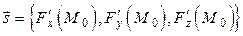 . Но эти же компоненты имеет и вектор
. Но эти же компоненты имеет и вектор 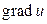 , следовательно, он направлен нормально к поверхности уровня скалярного поля.
, следовательно, он направлен нормально к поверхности уровня скалярного поля.
В плоском случае 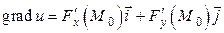 , и он ориентирован нормально к линиям уровня.
, и он ориентирован нормально к линиям уровня.
Для обозначения градиента скалярного поля часто используют векторный дифференциальный оператор 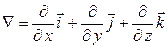 , который называется оператором Гамильтона или оператором набла. Формально умножив вектор набла на скалярное поле
, который называется оператором Гамильтона или оператором набла. Формально умножив вектор набла на скалярное поле 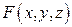 , получим равенство
, получим равенство
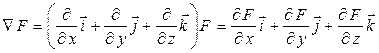
или
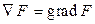 .
.
Следует иметь в виду свойства градиента, которые часто облегчают его вычисление:
1) 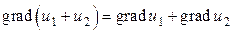 ;
;
2) 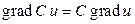 , где
, где  – константа;
– константа;
3) 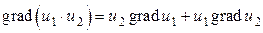 ;
;
4) 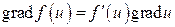 .
.
