Приближение геометрической оптики
При рассмотрении выражений для плоской (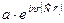 
) или сферической (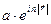 
) волн можно заметить, что в показателе экспоненты при множителе 
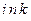находится выражение, являющееся функцией, описывающей 3х мерное уравнение поверхности, представляющей форму волнового фронта. Действительно 
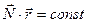и 
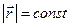представляют собой уравнения плоскости и сферы соответственно. Составим уравнение для произвольной функции 
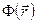волновой поверхности, называемой эйконалом при условии, что 
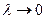. Выражение для комплексной амплитуды 
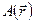будет
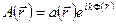. (5.1)
В случае больших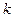 
(малых 
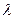) величина 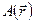изменяется очень быстро, из-за наличия в показателе комплексной экспоненты большого числа перед аргументом, в то время как амплитуда 
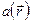и фаза (в данном случае эйконал) 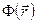меняются значительно медленнее. В этом случае, замена точного значения функции 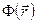ее приближенным значением скажется значительно слабее: влияние ошибки приближения уменьшится в отношении скоростей изменения функци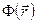й и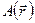 
. Раскладывая функцию 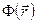в ряд Тейлора вблизи произвольной точки 
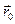и ограничиваясь первым членом, получим
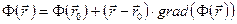. (5.2)
Теперь выражение (5.1) можно записать в виде
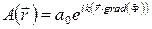, (5.3)
где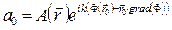 
.
На малых участках волнового фронта волну можно считать плоской
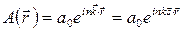. (5.4)
где введен единичный вектор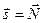 
, указывающий направления распространения волны. Сравнивая (5.4) и (5.3) получим
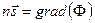. (5.5)
Вычисляя квадрат модуля от обеих частей (5.5) и учитывая, что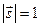 
. получим уравнение, эквивалентное (5.5)
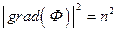. (5.6)
Получилось так называемое уравнение эйконала, причем 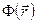входит в него в виде градиента. Из математики известно, что вектор градиента к функции в некоторой точке 
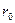направлен по нормали к ней, т.е. перпендикулярен касательной плоскости в этой точке. Таким образом, фактически, решение данного уравнения описывает траекторию луча, который может быть интерпретирован как нормаль к волновой поверхности. Именно это и лежит в основе математической модели геометрической оптики и в определении луча света, так как эти уравнения не содержат длины волны света.
Уравнение эйконала методами вариационного исчисления можно получить из принципа Ферма, который также может быть взят в виде основного постулата геометрической оптики. Этот принцип гласит, что между двумя точками свет распространяется по такой траектории, что бы затратить на это минимальное время, или что тоже самое, оптическая длина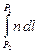 
луча между двумя точкам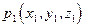и 
и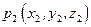 
короче любой другой кривой, соединяющей эти точки, лежащей в области, которую можно заполнить лучами так, что бы через каждую точку проходил только один луч.
С помощью принципа Ферма можно получить два основных закона оптики: закон отражения и закон преломления.
 |
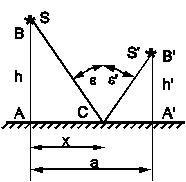Закон отражения. Пусть имеется отражающая поверхность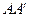 
. Построим траекторию луча между точкам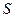и 
и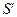 
. Оптическая длина между этими точками
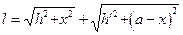. (5.7)
Минимум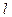 
достигается при условии равенства производной нулю, т.е.
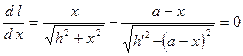. (5.8)
 |
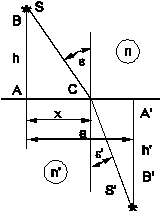Полученное равенство представляет собой пропорциональность соответственных сторон треугольников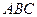 
и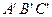 
, откуда следует равенство углов 
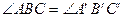и откуда непосредственно 
.
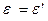Преломление. По аналогии с отражением, сумма длины оптических путей от 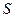до 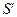определяется выражением (в соответствии с, принципом Ферма, оптическая длина пути равна геометрической, умноженной на показатель преломления)
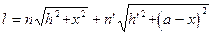
. (5.9)
Минимум оптического пути из равенства нулю производной
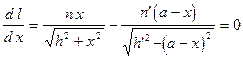. (5.10)
откуда, т.к.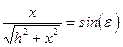 
, а 
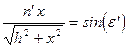, следует, что
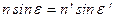. (5.11)
Данное выражение представляет собой закон преломления или закон Снеллиуса.
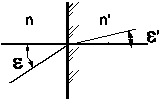
Отметим идентичность вывода формул для отражения и преломления: отражение можно считать частным случаем преломления, если положить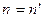 
, однако при этом как бы исчезает граница между средами и никакого преломления или отражения быть не должно. Это обстоятельство стало одной из причин введения в оптике правила знаков для углов, которое гласит, что если мысленно вращать к нормали по часовой стрелке, то этот угол положительный и наоборот. Например на рисунке 
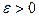, а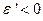 
. Тогда закон отражения можно записать как
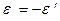. (5.12)
и считать, что показатель преломления среды после преломления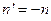 
.
 |
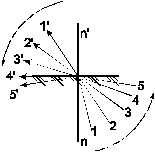
С помощью закона Снеллиуса можно объяснить явление полного внутреннего отражения. Прежде всего, из этого выражения следует, что угол преломления имеет обратную зависимость от показателя преломления, откуда вытекает правило - в более плотной среде луч прижимается к нормали. Т.е. если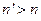 
, то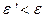 
. Если луч выходит из более плотной среды, то может наступить момент, когда 
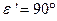, в этом случае преломленный луч пойдет по линии раздела двух сред; при дальнейшем увеличении угла 
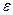луч будет отражаться и возвращаться в более плотную среду. Этот эффект и называется полным внутренним отражением. Предельный угол 
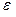получается из условия 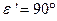. Подставляя это значение в (5.11), найдем что
 |
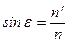
. (5.13а)
Если вторая среда - воздух, где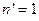 
, то
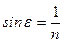. (5.13б)
В частности, для стекла марки К8, одного из самых распространенных в оптическом приборостроении, где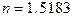 
, предельный угол будет
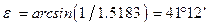. (5.14)
 |
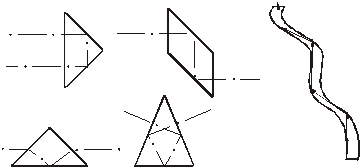Полное внутреннее отражение отличается тем, что энергетические потери при этом крайне малы и составляют доли процентов, в отличие от отражения от зеркал, где эти потери порядка нескольких десятков процентов. Это свойство используется в отражательных призмах, а также в волоконной оптике, где излучение распространяется на большие расстояния, отражаясь от стенок световода, испытывая полное внутреннее отражение. Явление полного внутреннего отражения применяется также при определения с большой точностью показателей преломления, например в рефрактометрах Пульфриха или Аббе.
Траектория (ход) луча
Одной из наиболее главных задач геометрической оптики является расчет хода луча. Под этим термином подразумевается нахождение траектории луча по оптической системе. Оптическая система же представляет собой ряд подпространств, ограниченных некоторыми поверхностями и заполненных однородными (иное специально оговаривается) средами с различными показателями преломления. Определим основные математические зависимости для такого расчета на основе уже сделанного физического обоснования. Ими являются траектория луча в среде между поверхностями и изменение направления на поверхностях - границах сред.
Рассмотрим уравнение эйконала (5.5)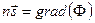 
. По определению 
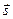перпендикулярен волновой поверхности 
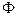(что, собственно и выражает это уравнение) и, соответственно, является касательным к лучу, т.е.
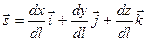 , | (6.1) |
так как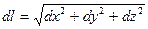 
. Таким образом уравнение эйконала можно записать в виде
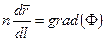 | (6.2) |
Если это уравнение продифференцировать по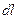 
, то (6.2) примет вид
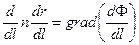 | (6.3) |
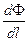можно преобразовать следующим образом:
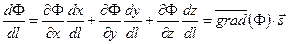 . | (6.4) |
Умножая обе стороны уравнения эйконала (5.5) скалярно на 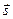и учитывая, что 
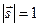, получим, что 
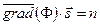. Подставляя в (3.6) окончательно получим дифференциальное уравнение
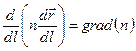 , | (6.5) |
решением которого является траектория луча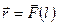 
как функция длины луча (т.н. натуральное уравнение) при любых заданных распределениях 
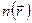показателя преломления в пространстве. Это уравнение используется для расчета хода луча в системах с неравномерным распределением показателя преломления, таких как линзоподобные среды, градиентные среды, турбулентная атмосфера и т.д. и т.п. В случае однородной среды 
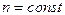, решение находится без труда, т.к. в этом случае 
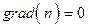, то решение очевидно
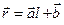. (6.6)
Получилось параметрическое уравнение прямой линии в пространстве, где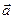 
и 
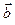произвольные векторы, которые являются постоянными интегрирования и могут быть получены из граничных условий. Их можно задать, полагая, что луч выходит из точки 
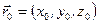в направлении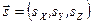 
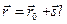, (6.7)
где параметр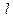 
имеет смысл длины луча от точки 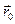до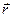 
, т.к. 
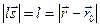. Приведенные выше рассуждение является доказательством прямолинейности распространения света в однородных средах, а так же дает способ задания луча в пространстве.
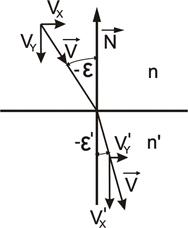
Выведем закон преломления для произвольно ориентированной поверхности раздела двух сред и луча. Направление луча (в изотропной среде) 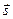определяется его скоростью 
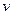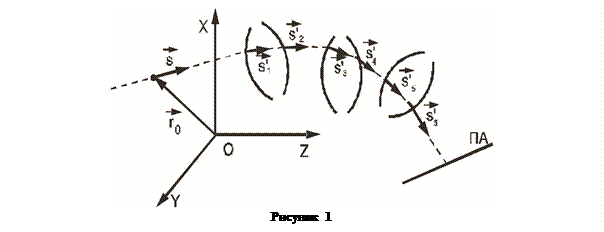
, т.е.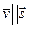 
. Из этого соотношения следует также и параллельность компононент скоростей и направляющих векторов в обоих подпространствах (рис 1).
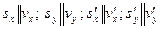 . | (6.8) |
Так как векторы 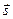и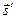 
единичные, то
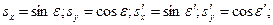 | (6.9) |
Вычислим выражение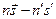 
. В компонентах это будет выглядеть следующим образом
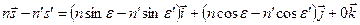 . | (6.10) |
В силу закона преломления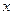 
компонента равна нулю, и искомое выражение имеет только 
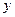компоненту, откуда следует, что вектор 
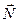коллинеарен 
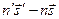и можно найти такую константу 
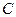, что
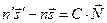. (6.11)
Откуда
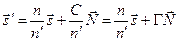, (6.12)
где константа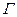 
носит название астигматической постоянной. Ее можно определить из условия, что 
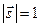. Вычисляя квадрат модуля обеих частей (6.12) и учитывая, что 
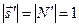, получим квадратное уравнение для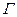
рис.1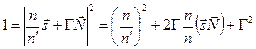 
(6.13)
Решая это уравнения и выбирая знак + перед радикалом, так как при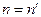 
направление луча не должно изменяться и подставляя 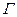в (6.12) получим
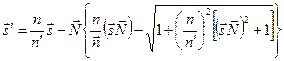(6.14)
Полученное выражение представляет собой так называемый закон преломления в векторной форме.
Для отражения можно поступить так же, как при выводе законов преломления и отражения, т.е. положив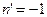 
(5.11-5.12), однако этого недостаточно, так как необходимо еще учесть преобразование пространства при зеркальном отражении. Это осуществится, если у 
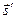изменить знак. Таким образом, закон отражения в векторном виде, т.е. при произвольных ориентациях луча и отражающей поверхности будет
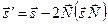. (6.15)
Формул (6.7),(6.13) и (6.15) оказывается достаточно для построения математической модели геометрической оптики, которая выглядит следующим образом. В некоторой, общей системе координат, своими уравнениями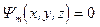 
задаются поверхности, где 
, ( 
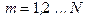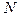число поверхностей), разделяющие области пространства,
заполненные однородными оптическими средами с заданными показателями преломлений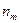 
(номер 
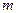присваивается подпространству и, соответственно, показателю преломления, следующему за поверхностью с номером 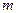по ходу луча). В этой же системе задается луч своей исходной точкой 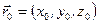(точкой предмета) и направлением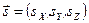 
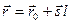, (6.16)
где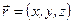 
.
В результате совместного решения уравнения луча (6.16) и уравнения первой поверхности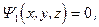 
находится точка их пересечения 
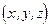, так называемая точка встречи. ( Как правило, после подстановки компонентов вектора 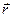в уравнение поверхности, сначала находят параметр 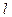- длину этого отрезка луча, а затем после подстановки его в (6.16), определяют и 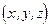). Затем, с помощью (6.13) или (6.15), находят направление отраженного или преломленного луча .
 |
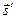Полагая найденные точку встречи 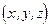и направление 
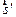в качестве исходных 
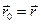и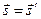 
повторяем процедуру нахождения точек встреч и новых направлений преломленного луча пока не достигнем последней поверхности оптической системы, после прохождения которой определим точку пересечения луча с поверхностью анализа (ПА) (поверхностью изображения). Затем, делая такие же вычисления для других лучей , найдем необходимое число таких точек пересечений, после чего проводится интерпретация результата.
Несмотря на относительную простоту модели геометрической оптики, аналитические выражения для компонент луча представляют собой чрезвычайно громоздкие формулы, сложность которых многократно возрастает при увеличении числа поверхностей. Существенные упрощения этих выражений наступает при использовании так называемых систем координат Федера, а также при расчете центрированных оптических систем с поверхностями не выше второй степени (в этом случае система уравнений сводится к квадратному уравнению), однако даже в этих случаях получаемые формулы практически непригодны для “ручного счета” и их используют для составления программ. Получение упрощенных выражений для расчета и анализа оптических систем и использование их является одной из основных задач прикладной оптики.
Однако имеется случай построения математической модели в виде аналитических выражений для реальной оптической системы состоящей из произвольного числа элементов. Это система из плоских зеркал, при этом в выражении (6.15) вектор нормали 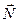постоянен, а направляющий вектор 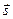входит в выражение линейно его как бы можно “вынести за скобки”. Благодаря этому удается разделить факторы, определяющие сигнал, в нашем случае луч света ( 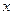компонента), и систему - зеркало ( 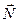). Это “вынесение” можно осуществить, используя методы и символику векторно-матричной алгебры, в которой обычный вектор представляется в виде матрицы, состоящей из одного столбца и 
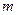строк (в нашем случае 
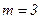). В такой записи выражение (6.15) примет вид
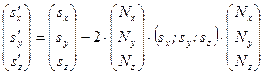. (6.17)
Второе слагаемое (без коэффициента 2) можно преобразовать, изменив порядок сомножителей, согласно правилу умножения матриц (сделав циклическую перестановку).
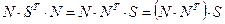, (6.18)
где -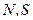 
-матрицы - столбцы, соответствующие векторам 
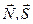- соответственно; индекс Т - означает транспонирование (в нашем случае эта операция переводит вектор - строку в вектор - столбец и наоборот). Результат умножения столбца на строку представляет собой квадратную матрицу, которая в нашем случае имеет вид
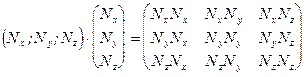. (6.19)
В такой форме, выражения (6.15) или (6.17) можно записать как
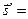
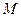
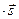, (6.20)
где 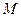- т.н. матрица отражений. Как следует из (6.14), выражение для нее имеет вид
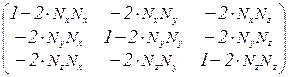. (6.21)
Если система состоит из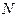 
плоских зеркал и каждое имеет свою матрицу отражений 
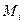, то всю систему можно представить в виде (6.21), где в качестве матрицы отражений будет матрица всей системы, которая получится как произведение матриц всех зеркал. Такое представление имеет большие преимущества при проектировании, анализе и оптимизации зеркальных систем.