Движение свободной микрочастицы
ФИЗИЧЕСКИЕ ОСНОВЫ НАНОЭЛЕКТРОНИКИ
Корпускулярно-волновой дуализм и принцип Гейзенберга.
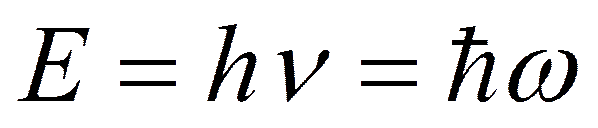
h- постоянная Планка
(h=6.62∙10-34Дж∙с, ħ=h/2𝛑);
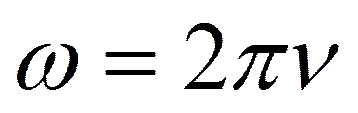- угловая частота
,
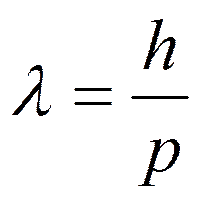
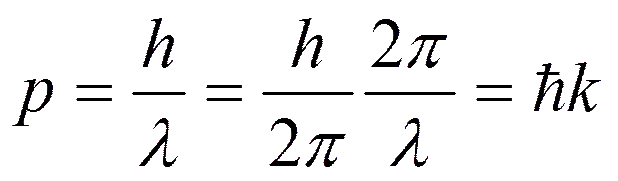где k- волновое число
Принцип неопределенности Гейзенберга, в соответствии с которым в любом эксперименте произведение ошибок измерения импульса частицы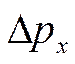 
и ее координаты 
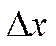всегда должно превышать 
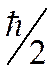, т.е.
· 
,
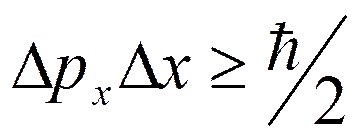
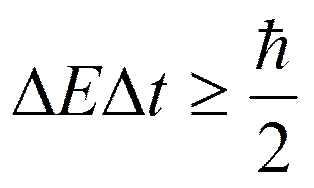
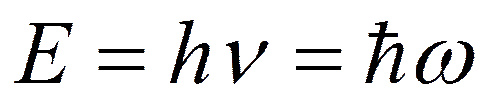где Е – энергия частицы,
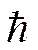- постоянная Планка.
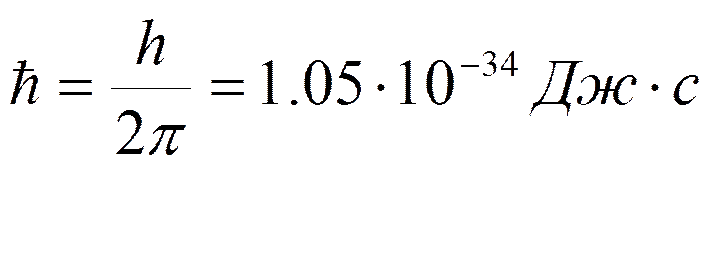
· Волновой вектор определяется импульсом
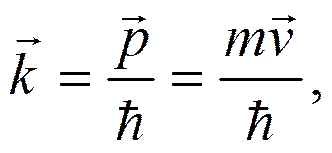
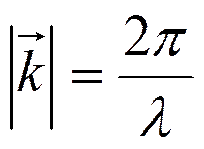
· Длина волны де Бройля
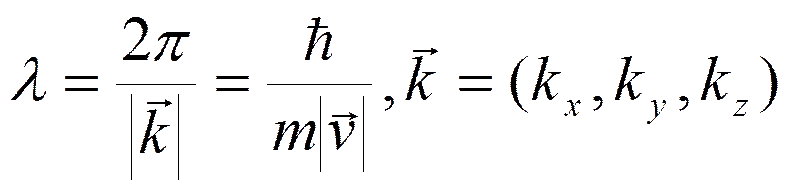
Т.о. де Бройль отождествил движущуюся материальную частицу с плоской электромагнитной волной следующего вида:
,
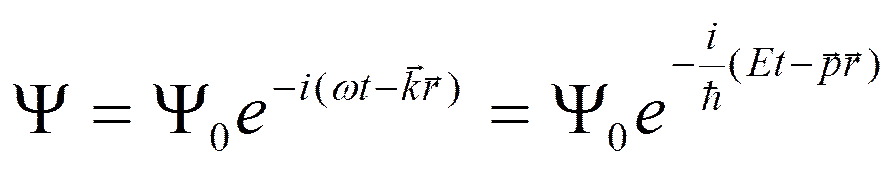где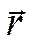 
- радиус-вектор
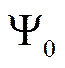- амплитуда плоской волны
Нанообъекты и волны де Бройля
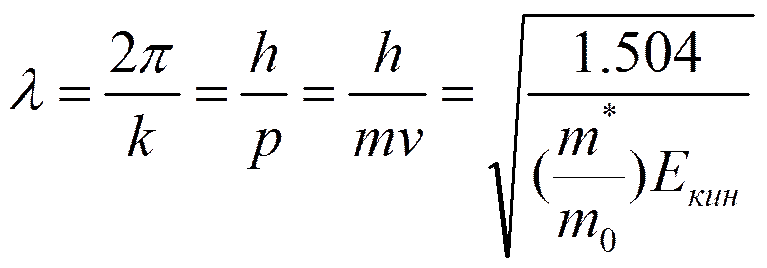
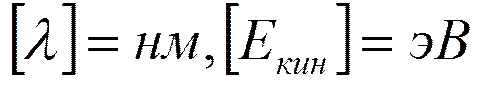
m0 – масса свободного электрона
m*- эффективная масса электрона
Кинетическая энергия при 300К Екин=kT=0.0259 эВ,
тогда λ=25 нм=250 Å
Т.о. если толщина тонких пленок или структур, из которых состоят нанообъекты соизмеримы с длиной волны де Бройля, то в таких объектах, называемых нанообъектами, можно ожидать проявления волновых свойств электрона
Волновые функции и уравнение Шредингера
Главная особенность квантово-механического описания электрона состоит в том, что электрон, оставаясь частицей, подобен волне (принцип де Бройля).
При этом его пространственные координаты и величину импульса невозможно определить с высокой точностью, т.е. невозможно предсказать направление, если известно, что в данный момент он расположен в какой-либо области пространства.
Поведение электрона теряет детерминированный характер, т.е. если в некоторый момент времени частица находилась в ограниченной области пространства, то в будущем невозможно достоверно предсказать ее местонахождение. Можно говорить лишь о распределении частиц в пространстве, о вероятности обнаружить ее в заданном месте.
Волновая функция –это функция, которая задает вероятностное статистическое описание местонахождения электрона в пространстве.
В общем случае уравнение Шрёдингера:
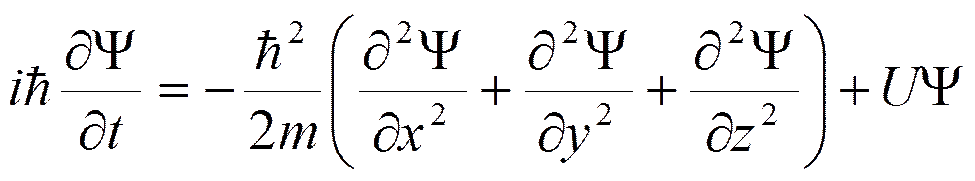
где
m- масса частицы,
U- потенциал поля, в котором движутся частицы
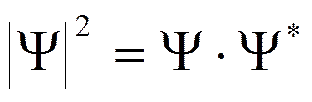
Вероятность обнаружения частицы в элементе объема
,
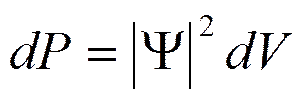если проинтегрировать это выражение по всему объему, получим условие нормировки уравнения Шредингера:
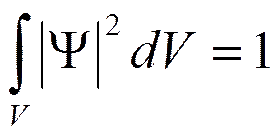
Если U не зависит от времени, то решение этого уравнения можно записать в виде
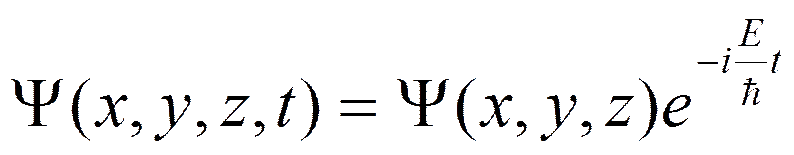
А стационарное уравнение Шредингера (не зависящее от времени) примет вид
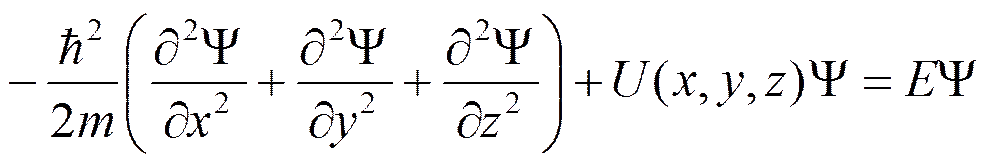
Движение свободной микрочастицы
Микрочастица называется свободной, если на нее не действуют никакие силы, т.е. U=0, тогда стационарное уравнение Шредингера можно записать в виде
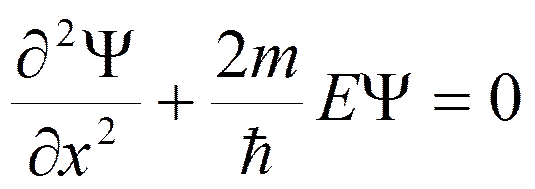
Если решать это уравнение относительно x, получим:
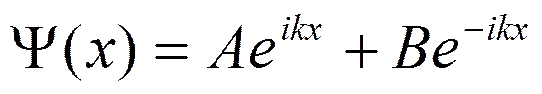
Для микрочастицы можно записать:
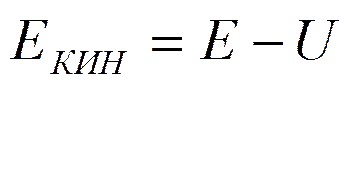
где Е- полная энергия электрона,
U- потенциальная энергия электрона
Для свободной частицы U=0, значит,
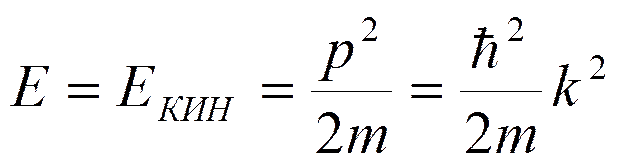
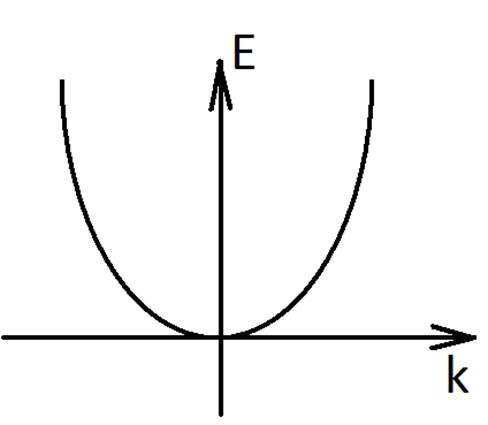
Зависимости энергии от волнового числа называются законами дисперсии.