Свойства сходящихся рядов.

Определение

Выражение называется рядом, а числа - элементы (члены) ряда.

Короткая форма записи 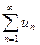, 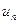- общий элемент ряда.

Ряд считается заданным, если известно правило, по которому для любого номера n можно записать соответствующий элемент ряда: . Если формула дана, то можно сразу записать любой элемент ряда.

Примеры:

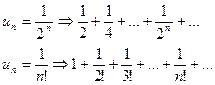
Иногда ряд задается при помощи рекурентного соотношения, которое связывает последующий член с предыдущими. Например

. Последовательно находим

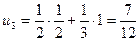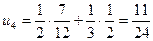, и так далее. Получаем ряд

Пусть дан ряд

- частичная сумма ряда.

Образуем последовательность частичных сумм ряда

С неограниченным увеличением числа n в сумме 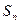учитывается все большее и большее число элементов ряда.

Определение

Если при 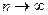существует предел последовательности частичных сумм данного ряда 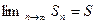, ряд называется сходящимся, число S - его суммой.

Запись

Если последовательность частичных сумм не стремится к пределу, то ряд называется расходящимся.

Замечание Ряд может расходиться в двух случаях:

1) Если последовательность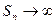

2) Если последовательность 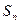вообще не имеет предела (ни конечного, ни бесконечного)

Пример

Рассмотрим сумму элементов бесконечной геометрической прогрессии

Если |q|<1, то . Следовательно, при |q|<1 бесконечная геометрическая прогрессия образует сходящийся ряд, сумма которого равна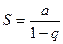

Если же |q|>1, то , то есть ряд расходится.

Пусть q=1. Ряд имеет . Ряд расходится.

Пусть q=-1. Ряд имеет , то есть 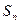не стремится ни к какому пределу.

Согласно определению это ряд расходится.

Таким образом, бесконечная геометрическая прогрессия представляет ряд, который сходится при |q|<1 и расходится, при .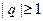

В рассмотренном примере сходимость и расходимость устанавливалась непосредственным определением сходимости и известной формулой для частичной суммы.

Однако в большинстве случаев это способ не применим, так как очень трудно найти компактную форму для 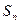, а значит и предел .

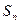Выяснять сходимость ряда можно с помощью признаков сходимости.

Рассмотрим сходящийся ряд

Определение

Разность между суммой ряда и его n-ой частичной суммой называется n-ым остатком ряда. Остаток ряда в свою очередь есть сумма бесконечного ряда. Обозначение

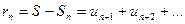
Исходный ряд по определению сходится, то есть 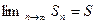следовательно, будет как угодно мало, если n взять достаточно большим.

Таким образом можно приближенно подсчитать сумму сходящегося ряда, взяв достаточно большое число первых его элементов. Однако большую трудность представляет выяснение величины возникающей ошибки.

Свойства сходящихся рядов.

1.Если ряд сходится и имеет сумму S, то ряд образованный из произведений всех элементов данного ряда на одно и то же число k:

также сходится и имеет сумму kS.

Доказательство

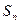- частичная сумма первого ряда;

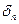- частичная сумма второго ряда.

2.Если сходятся ряды

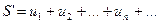
То ряд образованный сложением соответствующих элементов данных рядов то же сходится и его сумма равна S’+S”

Доказательство

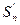- частичная сумма первого ряда;

- частичная сумма второго ряда;

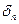- частичная сумма полученного ряда;

Тогда

Замечание

3.Если ряд сходится, то сходится и ряд, полученный из данного путем приписывания или отбрасывания любого конечного числа элементов.

Доказательство

Пусть ряд сходящийся.

Выбросим из него конечное число элементов, например, 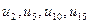(не меняя нумерации считаем, что на их места поставлены 0). Тогда при n>15 частичные суммы будут отличаться друг от друга на постоянное слагаемое . Если существует предел одной частичной суммы, то существует и предел второй, причем они отличаются друг от друга на постоянное слагаемое.

Совершенно аналогичные рассуждения в случае приписывания к ряду новых элементов.

Следствие Если сходится ряд, то сходится и любой его остаток, и наоборот.