Формулы и функции алгебры логики
Высказывания, образованные из элементарных переменных высказываний путем применения операций алгебры логики, называются сложнымивысказываниями или формуламиалгебры логики.
Если переменным, входящим в формулу задать определенные значения из множества {0,1},то и формула примет определенное значение из того же самого множества, отсюда, каждая формула алгебры логики определяет некоторую свою функцию,причем и аргументы и сама функция могут принимать лишь два значения 0 или 1.
Функцию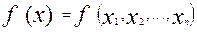 , принимающую значения 0 или 1 и определенную на всевозможных n-мерных наборах из 0 и 1, называют логической функциейили функцией алгебры логикиот n переменных.
, принимающую значения 0 или 1 и определенную на всевозможных n-мерных наборах из 0 и 1, называют логической функциейили функцией алгебры логикиот n переменных.
Любую функцию алгебры логики от n переменных можно представить с помощью специальной таблицы (таблицы истинности), в которой, для удобства, строки (их всего  ) располагаются в порядке возрастания двоичных чисел:
) располагаются в порядке возрастания двоичных чисел:
 |  | . . . . . |  |  |
| . . . . . |  | |||
| . . . . . |  | |||
| ... | ... | . . . . . | ... | . . . . . |
| . . . . . |  |
Теорема о числе функций алгебры логики от n переменных.
Числовсех функций алгебры логики от n переменных равно  .
.
Из теоремы о числе функций алгебры логики следует, что всех функций алгебры логики от двух переменных 16.
Рассмотрим эти функции.
| X | y |  |  |  |  |  |  |  | 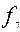 |  |  |  |  | 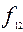 | 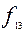 |  |  |
Здесь:
 =0 - “константа 0”,
=0 - “константа 0”,
 =x&y -“конъюнкция” (x и y)
=x&y -“конъюнкция” (x и y)
 =
=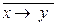 - “левая коимпликация” (не если x, то y).
- “левая коимпликация” (не если x, то y).
 =x - “переменная x”
=x - “переменная x”
 =
=  - “ правая коимпликация” (не если y, то x).
- “ правая коимпликация” (не если y, то x).
 =y - “переменная y”.
=y - “переменная y”.
 =x
=x  y=(
y=( 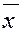 &y)V(x&
&y)V(x&  )- “сложение по модулю 2” (x плюс y по модулю 2).
)- “сложение по модулю 2” (x плюс y по модулю 2).
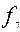 =xVy- “дизъюнкция” (x или y).
=xVy- “дизъюнкция” (x или y).
 =x
=x 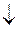 y=
y= 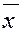 &
&  - “стрелка Пирса” (x стрелка y).
- “стрелка Пирса” (x стрелка y).
 =x~y= (
=x~y= ( 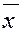 Vy)&(xV
Vy)&(xV  )- “эквивалентноcть” (x эквивалентно y).
)- “эквивалентноcть” (x эквивалентно y).
 =
= - “отрицание “ (не y).
- “отрицание “ (не y).
 =y
=y  x=
x=  Vx- “x правая импликация y, или y импликация x”
Vx- “x правая импликация y, или y импликация x”
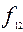 =
=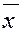 -“отрицание”(не x).
-“отрицание”(не x).
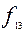 =x
=x  y=
y= 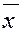 Vy - “ импликация ” (если x, то y).
Vy - “ импликация ” (если x, то y).
 =x|y=
=x|y= 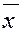 V
V  - “ штрих Шеффера” (x штрих y).
- “ штрих Шеффера” (x штрих y).
 =1- “константа 1”.
=1- “константа 1”.
Равносильные формулы. Законы алгебры логики.
Две формулы алгебры логики называются равносильными,если они принимают одинаковые значения при всех возможных значениях входящих в них переменных высказываний.
Законы алгебры логики.
Коммутативность
относительно конъюнкции относительно дизъюнкции
x&y=y&x xVy=yVx
Ассоциативность
относительно конъюнкции относительно дизъюнкции
(x&y)&z=x&(y&z) (xVy)Vz=xV(yVz)
Дистрибутивность
конъюнкции относительно дизъюнкции дизъюнкции относительно конъюнкции
x&(yVz)=(x&y)V(x&z) xV(y&z)=(xVy)&(xVz)
Закон де Моргана.
относительно конъюнкции относительно дизъюнкции


Законы поглощения
xV(x&y)=x
xV(  Vy)=xVy
Vy)=xVy
Законы идемпотентности
относительно конъюнкции относительно дизъюнкции
xVx=x x&x=x
Законы противоречия
относительно конъюнкции относительно дизъюнкции
x&  =0 xV
=0 xV  =1
=1
Законы констант
xV1=1
x&1=x
x&0=0
xV0=x
Для удобства записей выражений в алгебре логике в дальнейшем мы будем придерживаться следующих правил:
- если над некоторым выражением стоит отрицание, то это выражение мы не будем заключать в скобки;
- знак & мы будем иногда опускать (как знак операции пересечения в алгебре множеств);
- будем считать, что знак & “сильнее”, чем знаки дизъюнкции, сложения по модулю 2, эквивалентности, импликации, стрелки Пирса и штриха Шеффера, тем самым мы будем где это возможно, опускать скобки;
- на основании закона ассоциативности мы будем опускать скобки при записи нескольких идущих подряд дизъюнкций и конъюнкций.
