Кривые второго порядка
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных, называемых фокусами, есть величина постоянная, равная 2a, и большая чем расстояние между фокусами, равное 2c (рисунок 6).
 |
| Рисунок 6 |
Простейшее каноническое уравнение эллипса получается в системе координат, в которой за ось абсцисс выбрана прямая, соединяющая фокусы, начало координат 0 − середина отрезка, концами которого служат фокусы, ось ординат – прямая, проходящая перпендикулярно оси ОX через точку 0. Тогда уравнение эллипса примет следую-
щий вид:

где 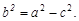
При таком выборе системы координат оси координат совпадают с осями симметрии эллипса, а начало координат − с центром симметрии. Точки А1(a; 0), А2(–a; 0), В1(0; b), В2(0; –b) называются вершинами эллипса. Отрезки, заключенные между вершинами, называются осями эллипса: большая (фокальная) ось А1А2 = 2a, малая ось В1В2 = 2b. Параметры a и b уравнения равны полуосям эллипса. Эксцентриситетом (e) эллипса называется отношение расстояния (2c) между фокусами к большей оси (2a), т. е. 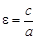 ; очевидно, что e< 1. Директрисами эллипса называются две прямые, параллельные малой оси и отстоящие от нее на расстоянии, равном
; очевидно, что e< 1. Директрисами эллипса называются две прямые, параллельные малой оси и отстоящие от нее на расстоянии, равном 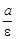 . Уравнения директрис сле-
. Уравнения директрис сле-
дующие: 
Пример 11. Составить каноническое уравнение эллипса, зная, что малая полуось равна 3 и эксцентриситет 
Решение
Уравнение будем искать в виде 
Из условия b = 3. Так как с одной стороны  , а с другой стороны по условию
, а с другой стороны по условию  то
то 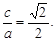 Откуда
Откуда 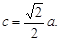 Для эллипса параметры a, b, c связаны соотношением
Для эллипса параметры a, b, c связаны соотношением 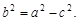 Поэтому, подставляя значения b и c, получим уравнение
Поэтому, подставляя значения b и c, получим уравнение
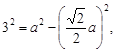
или
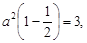
или
а2 = 6.
Ответ: 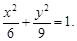
Тест 22. Уравнение эллипса, полуоси которого равны a = 3, b = 2, имеет вид:
1) 
2) 
3) 
Тест 23. Дано уравнение эллипса 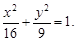
Вычислить длину осей, фокусное расстояние, эксцентриситет:
1) 16; 9; 25; 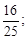
2) 8; 6; 2 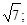

3) 4; 3; 1; 8.
Пример 12. Дан эллипс  Написать уравнение его директрис.
Написать уравнение его директрис.
Решение
Уравнения директрис следующие: 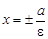 . Из уравнения а2 = 36,
. Из уравнения а2 = 36,
b2 = 20. Следовательно, a = 6, 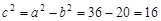 или с = 4. Найдем e =
или с = 4. Найдем e =  Подставим в уравнения
Подставим в уравнения 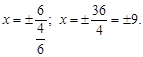
Ответ: x = ±9.
Уравнение эллипса, центр которого находится в точке (х0; у0), а оси симметрии параллельны осям координат, имеет вид

Тест 24. Центр эллипса 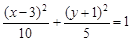 находится в точке:
находится в точке:
1) (3; 1);
2) (3; –1);
3) (10; 5);
4) (5; 10).
Гиперболой называется множество точек плоскости, модуль разности от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2a, и меньшая чем расстояние между фокусами, равное 2c (рисунок 7).
 |
Рисунок 7
Простейшее каноническое уравнение гиперболы имеет вид
 (1)
(1)
где b2 = c2 – a2.
Прямая, соединяющая фокусы F1, F2 гиперболы, служит осью абсцисс, начало координат находится в середине между фокусами; при этом оси координат совпадают с осями симметрии гиперболы, начало координат – с ее центром симметрии (оси и центр гиперболы).
Гипербола имеет две действительные вершины А1(a; 0), А2(–a; 0) на фокальной оси; отрезок А1А2 = 2a называется действительной осью гиперболы, отрезок В1В2 = 2b – мнимой осью гиперболы. Таким образом, параметры a и b в уравнении гиперболы равны длинам действительной и мнимой полуосей соответственно.
Если a = b, то гипербола называется равносторонней.
Если мнимая ось гиперболы имеет длину 2a и направление по оси x, а действительная ось, длиной 2b, совпадает с осью y, то уравнение такой гиперболы имеет следующий вид:
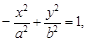 (2)
(2)
где 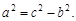
Гиперболы (1) и (2) называются сопряженными гиперболами.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к действительной оси: e =  и при этом e > 1. Директрисами гиперболы называются прямые, перпендикулярные к фокальной оси и отстоящие на расстоянии, равном
и при этом e > 1. Директрисами гиперболы называются прямые, перпендикулярные к фокальной оси и отстоящие на расстоянии, равном  Уравнения директрис следующие:
Уравнения директрис следующие: 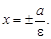 Асимптоты гиперболы определяются равенствами
Асимптоты гиперболы определяются равенствами 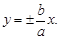
Если точка, двигаясь по гиперболе, неограниченно удаляется, то расстояние ее от одной из асимптот стремится к нулю. Асимптоты являются диагоналями прямоугольника со сторонами 2a, 2b (рисунок 7).
Пример 13.Составить уравнение гиперболы, оси которой совпадают с осями координат, зная, что:
1. Расстояние между вершинами равно 8, а расстояние между фокусами – 10.
2. Действительная ось равна 6, гипербола проходит через точку
(9; –4).
Решение
1. Уравнение гиперболы имеет вид 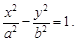
Так как расстояние между вершинами равно 8, то 2a = 8 или a = 4. Учитывая, что расстояние между фокусами равно 10, имеем 2c = 10, откуда c = 5. Найдем b2 из соотношения b2 = c2 – а2, т. е. b2 = 52 – 42 =
= 25 – 16 = 9.
Ответ: 
2. Так как действительная ось равна 6, то 2a = 6 или a =3. Поэтому уравнение гиперболы принимает вид  Поскольку гипербола проходит через точку (9; –4), то ординаты этой точки обращают уравнение в истинное равенство, т. е.
Поскольку гипербола проходит через точку (9; –4), то ординаты этой точки обращают уравнение в истинное равенство, т. е. 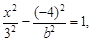 или
или 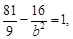 или 9 – 1 =
или 9 – 1 =  или b2 =
или b2 =  = 2.
= 2.
Ответ: 
Тест 25. Уравнение гиперболы, действительная ось которой равна 10 и лежит на оси ОX, а мнимая ось равна 16 и лежит на оси ОY, имеет вид:
1) 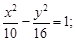
2) 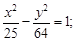
3) 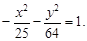
Тест 26. Дано уравнение гиперболы 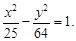 Вычислить длину осей, фокусное расстояние, эксцентриситет:
Вычислить длину осей, фокусное расстояние, эксцентриситет:
1) 10; 16; 2 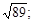
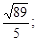
2) 4; 5; 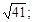

3) 5; 4; 
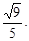
Пример 14. Дана гипербола 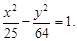 Написать уравнение ее директрис и асимптот.
Написать уравнение ее директрис и асимптот.
Решение
Из уравнения а2 = 16, b2 = 25. Откуда a =4, b =5. Найдем 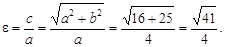 Тогда уравнения директрис следующие:
Тогда уравнения директрис следующие: 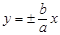 , или x =
, или x =  , или x =
, или x = 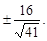
Уравнения асимптот  после подстановки a, b принимают вид y =
после подстановки a, b принимают вид y = 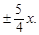
Ответ: x = 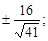 y =
y = 
Тест 27. Указать, принадлежит ли точка (0; 2) гиперболе  = 1:
= 1:
1) да;
2) нет.
Уравнение гиперболы, центр которой находится в точке (х0; у0), действительная ось совпадает с осью ОX, мнимая – с осью ОY, имеет вид
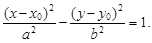
Тест 28. Центр гиперболы  находится в точке:
находится в точке:
1) (5; 7);
2) (–5; –7);
3) (9; 16);
4) (3; 4).
Ответы на тестовые задания
| Номер теста | |||||||
| Правильный ответ |
Парабола
Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом параболы, и данной прямой, называемой директрисой параболы (рисунок 8).
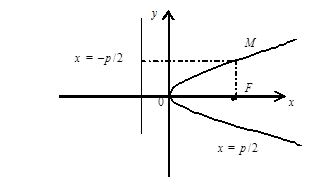 |
| Рисунок 8 |
Если за ось абсцисс принять перпендикулярную прямую, проведенную из фокуса к директрисе, а начало координат поместить посередине между фокусом и директрисой, то уравнение параболы примет вид
у2 = 2рх,
где р – параметр параболы, расстояние от фокуса параболы до ее директрисы.
Парабола имеет одну ось симметрии, которая совпадает при таком выборе системы координат с осью X. Единственная вершина параболы совпадает с началом координат и является единственной точкой пересечения параболы с осями.
Пример 15. Составить уравнение параболы, зная, что фокусы имеют координаты (0; 5), ось ординат служит осью симметрии, а вершина находится в начале координат.
Решение
Так как осью симметрии является ось ОY, то уравнение будет иметь вид х2 = 2ру, так как фокус в общем случае имеет координаты 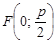 , то исходя из условия имеем
, то исходя из условия имеем 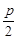 = 5, откуда p = 10. Таким образом, х2 = 2 × 10 × у или х2 = 20у – искомое уравнение.
= 5, откуда p = 10. Таким образом, х2 = 2 × 10 × у или х2 = 20у – искомое уравнение.
Тест 29. В уравнении параболы у 2 = 3х значение параметра p равно:
1) 3;
2) 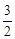 ;
;
3) 1;
4) 3x.
Тест 30. Среди уравнений второго порядка указать уравнение гиперболы:
1) 
2) 
3) 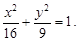
Если вершина параболы находится в точке (x0; y0), то ее каноническое уравнение примет следующий вид:

Ответы на тестовые задания
| Номер теста | ||
| Правильный ответ |
Векторная алгебра
При изучении различных разделов экономики, механики, физики, других учебных дисциплин приходится иметь дело с величинами, для характеризации которых в выбранной системе единиц достаточно указать их численные значения. Эти величины называются скалярными. К числу скалярных величин можно отнести длину, площадь, объем, массу, температуру и т. п. Встречаются, тем не менее, такие величины, для определения которых необходимо знать их направления в пространстве. Указанные величины будем называть векторными. Примерами векторных величин являются сила, скорость, ускорение.
Геометрические векторные величины изображаются с помощью направленных отрезков.
Связанным вектором (или направленным отрезком) называется любой отрезок прямой, если только указано, какая из двух ограничивающих его точек является начальной, какая – конечной. Если точка А – начало отрезка, а точка В – его конец, то связанный вектор будем обозначать 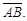 Его направление будем указывать стрелкой, идущей от начала А к концу В.
Его направление будем указывать стрелкой, идущей от начала А к концу В.
Длиной 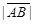 (или модулем) связанного вектора
(или модулем) связанного вектора 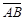 называется длина отрезка АВ. Связанный вектор, у которого начало и конец совпадают, называется нулевым. Нулевой вектор обозначается 0, его длина равна 0:
называется длина отрезка АВ. Связанный вектор, у которого начало и конец совпадают, называется нулевым. Нулевой вектор обозначается 0, его длина равна 0: 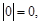 он направления не имеет.
он направления не имеет.
Связанные векторы 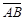 и
и 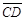 называются сонаправленными, если являются сонаправленными лучи
называются сонаправленными, если являются сонаправленными лучи 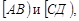 и противоположно направленными – если противоположно направлены эти лучи.
и противоположно направленными – если противоположно направлены эти лучи.
Два ненулевых связанных вектора 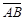 и
и 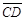 назовем равными (это обозначается
назовем равными (это обозначается 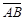 =
= 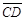 ), если они сонаправлены и имеют одинаковую длину.
), если они сонаправлены и имеют одинаковую длину.
Свободным вектором а (или просто вектором) назовем множество равных между собой связанных векторов. При дальнейшем из контекста будет ясно, какой вектор имеется в виду (связанный или свободный). Для задания вектора достаточно указать какой-либо один вектор из всего множества {AB, CD, MN, ¼} равных связанных векторов, например, 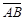 (рисунок 9).
(рисунок 9).
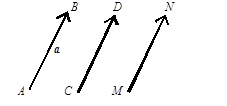
Рисунок 9
Рассмотренные понятия (длина, направление и т. п.), которые введены для связанных векторов, имеют аналоги также и для свободных. Часто векторы обозначают одной жирной строчной буквой: 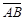 = а (рисунок 10).
= а (рисунок 10).
Линейные операции над векторами
Определим для свободных векторов операции их сложения, вычитания, умножения вектора на действительное число.
Суммой двух векторов a и b по правилу треугольника называется такой третий вектор с, что начало его совпадает с началом вектора а, а конец – с концом вектора b.
Иногда вместо с = а+bпишут 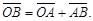 Суммой а1 +а2 +…
Суммой а1 +а2 +…
… + аn конечного числа векторов называется такой вектор а, который замыкает ломаную линию, построенную из данных векторов а1, а2,…, аn таким образом, что начало каждого последующего вектора совпадает с концом предыдущего. Указанный вектор а направлен из начала первого вектора суммы в конец последнего (правило многоугольника) (рисунок 10).
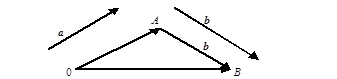
c = a + b
Рисунок 10
На рисунке 11 изображена сумма а = а1 + а2 + а3 + а4 + а5 векторов а1, а2, а3, а4, а5.
Произведением вектора а на число a называется вектор b = a а, длина которого равна 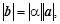 направление которого совпадает с направлением а, если a > 0, и противоположно направлению а, если
направление которого совпадает с направлением а, если a > 0, и противоположно направлению а, если
a < 0. По определению a а × 0 = 0 для любого a и 0 × а = 0 для любого а. На рисунке 12 изображены векторы а, 3а,–2а.
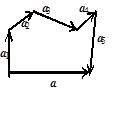 Рисунок 11 Рисунок 11 |  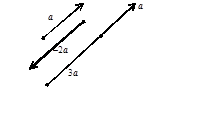 Рисунок 12 Рисунок 12 |
Векторы а, b, с называются коллинеарными, еслиих соответ-
ствующие связанные векторы параллельны одной и той же прямой. На рисунке 12 изображены коллинеарные векторы а, –2а, 3а.
Векторы а, b, с называют компланарными, если их соответствующие связанные векторы параллельны одной и той же плоскости (рисунок 13).
Углом jмежду векторами а и bназывается величина наименьшего угла между связанными векторами 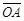 и
и  (рисунок 14). Понятно, что 0 £ j £ 0. Если
(рисунок 14). Понятно, что 0 £ j £ 0. Если 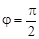 , то векторы а и b называются ортогональными (перпендикулярными, это обозначается а ^ b).
, то векторы а и b называются ортогональными (перпендикулярными, это обозначается а ^ b).

Разностью а – bназывается вектор с, равный сумме векторов а и
–1b = –b, т. е. с = а–b = а+(–b). Итак, по определению, чтобы вычесть из вектора а вектор b, необходимо к вектору а прибавить вектор –b, который называется противоположным вектору b. Из рисунка 15 следует, что если на векторах а и b, приведенных к общему началу, построить параллелограмм как на сторонах и провести диагонали, то диагональ параллелограмма, исходящая из общего начала векторов а и b,равна их сумме а + b, а другая диагональ – их разности а– b.
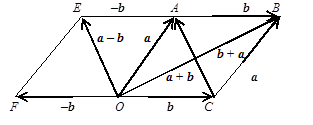
Рисунок 15
Данный способ нахождения суммы а+ b векторов аи b называется правилом параллелограмма.
Вектор, длина которого равна единице, будем называть единичным вектором, или ортом. Через а0 будем обозначать единичный вектор, имеющий направление вектора а.
