Расчет балки, подверженной косому

Н. Б. ЛЕВЧЕНКО

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

ЧАСТЬ 3

Санкт-Петербург

Министерство образования и науки Российской Федерации

Санкт-Петербургский государственный архитектурно-строительный

университет

Автомобильно-дорожный факультет

Кафедра сопротивления материалов

Н. Б. ЛЕВЧЕНКО

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Учебное пособие по выполнению расчетно-графических

работ для студентов всех специальностей и форм обучения

ЧАСТЬ 3

Задачи № 28–38

Под редакцией д-ра техн. наук, проф. В. Д. Харлаба

Санкт-Петербург

УДК 539.3/8(07)

Сопротивление материалов:Учебное пособие по выполнению расчетно-графических работ для студентов всех специальностей и форм обучения. Ч. 3./ Н. Б. Левченко; СПбГАСУ. СПб., 2011. с.

В пособии даны краткие сведения из теории, необходимые для решения задач, и приводятся примеры решения задач, входящих в расчетно-графические работы, по 3 темам: "Сложное сопротивление", "Устойчивость", "Расчет на динамическую нагрузку". Решение задач снабжено подробными объяснениями.

Ил. 49. Библиогр.: 9 назв.

Рецензенты:

д-р техн. наук, проф. В. З. Васильев (Санкт-Петербургский государственный университет путей сообщения);

д-р техн. наук, проф. В. В. Улитин (Санкт-Петербургский государственный университет низкотемпературных и пищевых технологий)

Рекомендовано Редакционно-издательским советом СПбГАСУ в качестве учебного пособия

© Н. Б. Левченко, 2011

© Санкт-Петербургский государственный

архитектурно-строительный университет, 2011

ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ

В процессе изучения курса "Сопротивление материалов" студенты выполняют расчетно-графические работы (РГР). Количество РГР и задач, входящих в каждую из этих работ, зависит от специальности и количества часов, отведенных в учебном плане на изучение курса. Цель РГР – сознательное усвоение теоретического курса и приобретение навыков решения задач, имеющих как академический, так и практический характер.

Данное учебное пособие предназначено для оказания помощи студентам при выполнении расчетно-графических работ. Номера задач, решение которых объясняется в данном пособии, соответствуют номерам задач в методических указаниях [4], по которым студенты выбирают схемы решаемых задач.

В данном пособии приводятся краткие теоретические сведения и основные формулы, необходимые для выполнения задач, объясняются смысл и порядок решения задач. Решение одних задач сопровождается численными расчетами, решение других приведено в общем виде. Ни в коем случае не следует копировать решение задач, не разобравшись со смыслом того, что Вы делаете. Пособие не заменяет учебник, поэтому перед выполнением задач прочитайте те разделы учебников, которые приведены в перечне литературы по изучаемой теме. В процессе расчетов обращайте внимание на единицы измерения величин, входящих в формулы. Не забывайте писать, в каких единицах Вы получили результат. Рекомендуемые единицы измерения приведены в перечне используемых обозначений. Все арифметические вычисления следует выполнять с точностью до трех значащих цифр – точностью, достаточной для инженерных расчетов.

Расчетно-графические работы оформляются на одной стороне стандартных листов писчей бумаги формата А-4 (210х297). Перед решением задачи необходимо нарисовать расчетную схему задачи в масштабе в соответствии со своими данными. Решение задачи должно сопровождаться короткими пояснениями, рисунки желательно делать карандашом, на листах должны быть оставлены поля для замечаний преподавателя. После выполнения всех задач, входящих в расчетно-графическую работу, листы с решением следует сброшюровать и снабдить титульным листом.

ИСПОЛЬЗУЕМЫЕ ОБОЗНАЧЕНИЯ

Нагрузки:

F – сосредоточенная сила, кН;

M – сосредоточенная пара сил (момент), кН×м;

q – интенсивность распределенной по длине стержня нагрузки, кН/м.

Обозначение осей:

x – продольная ось стержня;

y, z – главные центральные оси инерции поперечного сечения стержня.

Геометрические характеристики поперечного сечения стержня:

A – площадь поперечного сечения, см²;

S_y, S_z – статические моменты относительно осей 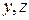, см³;

I_y, I_z – осевые моменты инерции относительно осей 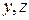, см⁴;

I_p – полярный момент инерции, см⁴.

Внутренние усилия:

N – продольная сила, кН;

Q_y , Q_z , (Q)– поперечные силы, кН;

M_y , M_z, (M)– изгибающие моменты, кН×м;

M_к – крутящий момент, кН×м.

Напряжения:

s_x, s_y, s_z, (s) – нормальные напряжения, МПа;

t_xy, t_yz, t_zx, (t) – касательные напряжения, МПа;

s₁, s₂, s₃, (s_гл) – главные напряжения, МПа.

Деформации и перемещения:

e_x, e_y, e_z, (e) – относительные линейные деформации;

g_xy, g_yz, g_zx, (g) – угловые деформации (углы сдвига);

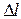– абсолютная деформация стержня при растяжении-сжатии (перемещение точек оси вдоль оси x), см;

v, w – прогибы оси стержня (балки) при изгибе (перемещения точек оси вдоль осей y, z), см;

j – угол поворота оси стержня (балки) при изгибе, рад;

q – угол закручивания стержня (вала) при кручении, рад.

Характеристики материала:

s_пц – предел пропорциональности, МПа;

s_т – предел текучести, МПа;

s_в – временное сопротивление (для хрупких материалов 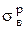– предел прочности при растяжении, 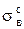– предел прочности при сжатии), МПа;

[s], [t] – допускаемые напряжения, МПа;

E – модуль упругости, МПа;

n – коэффициент Пуассона;

a – коэффициент линейного температурного расширения, 1/град.

СЛОЖНОЕ СОПРОТИВЛЕНИЕ

Рекомендуемая литература

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 6 (§ 6.5, § 6.6), гл.4.

Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 7, 15.

Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 9.

Основные понятия и формулы

Сложное сопротивление – такой вид деформации, при котором в стержне могут возникнуть все шесть видов внутренних усилий одновременно. Эти усилия определяются, как обычно, методом сечений. При построении эпюр внутренних усилий правила знаков для продольной силы и крутящего момента используем те же, что и раньше. Для изгибающих моментов принимается другоеправило знаков, а именно: изгибающий момент считается положительным, если он вызывает растягивающие напряжения в положительном квадранте (т. е. в том квадранте, где координаты 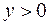и 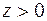). Поперечная сила считается положительной, если она действует по направлению ос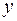и (или 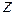) и находится в сечении, внешняя нормаль к которому совпадает по направлению с осью 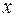. Рис. 5.1 поясняет правила знаков для всех внутренних усилий.

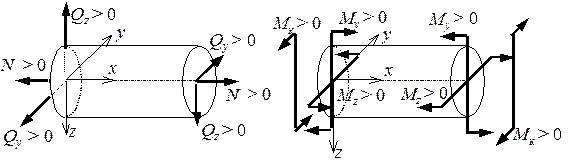Рис. 5.1. Правила знаков для внутренних усилий в задачах сложного сопротивления

От действия всех внутренних усилий в поперечном сечении стержня возникают нормальные и касательные напряжения. Нормальные напряжения связаны с действием продольной силы и изгибающих моментов и определяются в любой точке поперечного сечения[1] по формуле

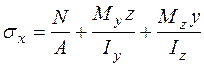. (5.1)

Здесь 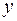и 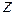– координаты той точки, в которой находятся напряжения, в главной центральной системе координат; 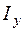, 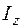– осевые моменты инерции относительно главных центральных осей. При использовании приведенного выше правила знаков для изгибающих моментов формула (5.1) автоматически дает знак напряжений при подстановке координат точки со своим знаком независимо от направления осей. Напомним, что положительный знак напряжений говорит о том, что в рассматриваемой точке действует растягивающее напряжение.

При расчете конструкций нас, как правило, интересуют максимальные напряжения. Точки, в которых они действуют, называются опасными. Для определения положения опасных точек с максимальными (растягивающими или сжимающими) нормальными напряжениями надо построить нейтральную линию и найти точки, наиболее удаленные от нее. Напомним, что нейтральной линией называется линия, на которой нормальные напряжения равны нулю. Для построения нейтральной линии запишем ее уравнение, приравняв напряжения в формуле (5.1) нулю:

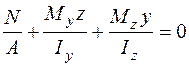. (5.2)

В уравнении (5.2) y и z – координаты точек, принадлежащих нейтральной линии. Построив по уравнению (5.2) нейтральную линию, проведем прямые, касательные к контуру сечения и параллельные нейтральной линии. Точки касания этих прямых контура сечения и являются опасными точками, в которых действуют максимальные нормальные напряжения. Рис. 5.2 поясняет описанное построение для сечения произвольной формы. Показанная на рис. 5.2 эпюра нормальных напряжений соответствует положительным значениям усилий в уравнении (5.2). Максимальное напряжение действует в точке 1, именно эта точка и будет опасной. Для определения нормальных напряжений в этой точке подставим в формулу (5.1) координаты 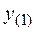и 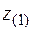этой точки (см. рис. 5.2). Заметим, что при отрицательной (сжимающей) продольной силе максимальные сжимающие напряжения будут по модулю больше растягивающих. В этом случае для хрупких материалов опасными будут обе точки: и точка 1, и точка 1¢ (см. рис. 5.2).

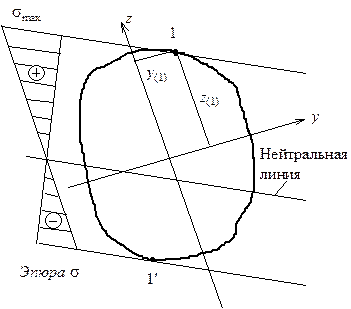Рис. 5.2. Определение положения опасных точек с максимальными нормальными напряжениями

От поперечных сил в сечении стержня возникают касательные напряжения, которые определяются по формуле Журавского в тех случаях, когда она применима (т. е. когда t можно считать равномерно распределенными по ширине сечения, что приемлемо, если Q действует по оси симметрии сечения или сечение является тонкостенным). Как известно из опыта расчета конструкций при плоском поперечном изгибе, касательные напряжения от поперечной силы, как правило, существенно меньше нормальных напряжений, поэтому в задачах сложного сопротивления при проверке прочности их чаще всего не учитывают.

Крутящий момент вызывает в сечении касательные напряжения. Формулы для определения этих касательных напряжений зависят от формы поперечного сечения и изучались ранее. Эти формулы для двух наиболее часто применяемых форм сечения – круглого и прямоугольного – будут рассмотрены в разд. 5.3 "Общий случай сложного сопротивления".

Чаще всего в реальных конструкциях встречаются два частных случая сложного сопротивления: косой (или пространственный) изгиб и внецентренное растяжение-сжатие. В разд. 5.1 и 5.2 рассматриваются эти виды деформаций, разд. 5.3 описывает проверку прочности конструкций в общем случае сложного сопротивления.

РАСЧЕТ БАЛКИ, ПОДВЕРЖЕННОЙ КОСОМУ