Решение (алгебраический способ)
Алгебраическое решение уравнения (1) стандартно, но трудоемко. Приведем его подробно.
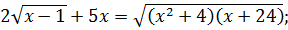
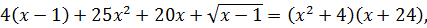
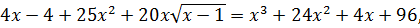
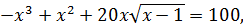
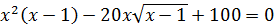
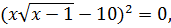
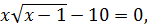
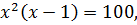
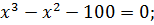 путем подбора находим число, при котором выполняется равенство
путем подбора находим число, при котором выполняется равенство 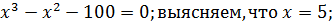
Разделим правую часть неравенство на 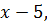 деление выполняется без остатка; частное от деления
деление выполняется без остатка; частное от деления 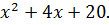 Уравнение
Уравнение 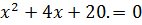 не имеет действительных корней.
не имеет действительных корней.
Ответ:5.
Применение формулы расстояния между двумя точками.
Пример 4. Решить систему уравнений
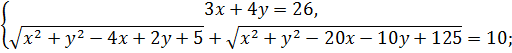
Решение (геометрический способ).
Рассмотрим слагаемые второго уравнения.
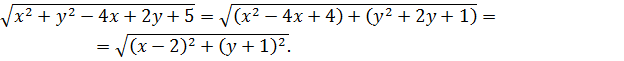
Пусть это расстояние между «текущей» точкой М(х;у) и точкой А(2;-1).
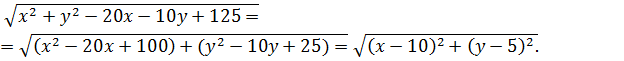
Пусть это расстояние между точками М(х;у) и В(10;5). Найдём расстояние между точками А и В: 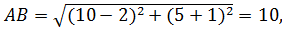
Откуда следует, что 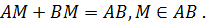 Составим уравнение прямой АВ, проходящей через точки А и В.
Составим уравнение прямой АВ, проходящей через точки А и В.
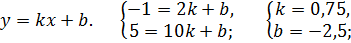
Имеем : 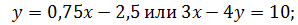 Получим новую систему:
Получим новую систему:
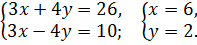
Ответ: (6;2).
Решение (алгебраический способ)
Решение данной системы алгебраическим способом оказалось очень трудоемким и нерациональным. Привожу только его начало.
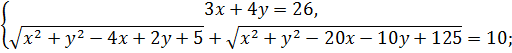
1) 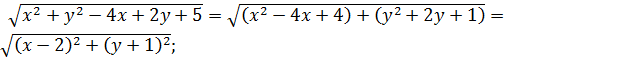
2) 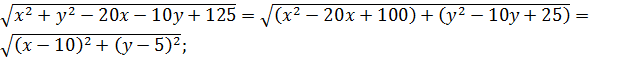
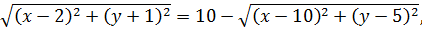
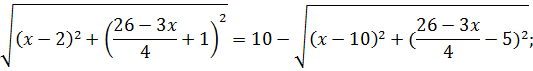
После дальнейших преобразований стало очевидно, что решать уравнение аналитически - нерационально. Поэтому решение было остановлено.
Анализ рациональности решения уравнений и систем геометрическим способом.
Попробуем обобщить сказанное и сделанное выше. Я думаю, что геометрический способ решения уравнений и систем в алгебре, как правило, не усложняет их. Основной трудностью при его применении является неочевидность, особенно в примере (3). Ведь до применения векторов нужно додуматься или просто знать о такой возможности. Все уравнения и системы, рассмотренные мной в работе (кроме последней), имеют стандартное алгебраическое решение. Поэтому в условиях экзамена, при дефиците времени, понятно, по какому пути многие пойдут. Поэтому рациональность геометрического способа – вопрос спорный. Однако, при решении системы в примере (4), этот способ – единственно возможный, кроме того, он еще и красив! Тем более, что формула расстояния между двумя точками легко узнаваема.
При решении системы из примера 1 геометрический способ становится эффективным, если в условии не требуется находить решения системы, а, например, значения x + z, y(x +z) и так далее. Тогда из геометрического чертежа ответы на эти вопросы становятся очевидными.
Еще одна легко узнаваемая теорема может применяться при решении иррациональных уравнений. Это теорема косинусов. Ей посвящена вторая часть моей работы.
Иррациональные уравнения и теорема косинусов.
Покажем, как можно решить некоторые иррациональные неравенства, используя всего одно геометрическое средство: теорему косинусов.
Пример5.Решите уравнение:
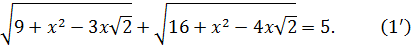
Решение.
Сначала докажем, что выполняется неравенство: 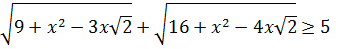 Заметим, что если Заметим, что если 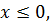 то то | 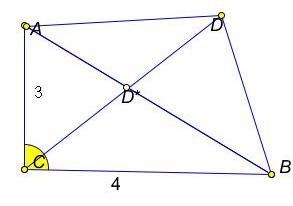 |
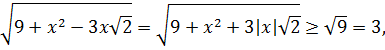
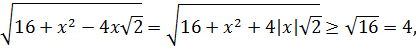
Поэтому значение левой части неравенства в этом случае не меньше, чем 3+4=7.
Чтобы убедиться в истинности неравенства при 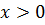 , рассмотрим треугольник ACD, в котором АС=3, CD=x, a угол ACD =
, рассмотрим треугольник ACD, в котором АС=3, CD=x, a угол ACD = 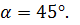 В силу теоремы косинусов имеем:
В силу теоремы косинусов имеем:
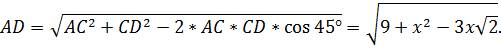
Аналогично, если СВ=4, CD=x, а угол BCD = 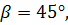 то из треугольника ВСD имеем DB =
то из треугольника ВСD имеем DB = 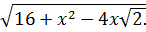
Так как угол АСВ – прямой, то 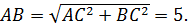 Следовательно, с помощью неравенства треугольника получаем:
Следовательно, с помощью неравенства треугольника получаем:
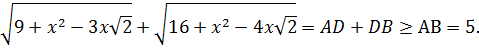
Таким образом, в основу неравенства (1) положен египетский треугольник, т.е. прямоугольный треугольник со сторонами 3, 4, 5.
Равенство(1’) не может быть истинным при 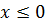 , а при x>0 значение его левой части равно
, а при x>0 значение его левой части равно 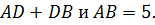 Ясно, что
Ясно, что 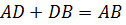 в том, и только том случае, когда точка D лежит на отрезке АВ. Следовательно, поскольку CD – биссектриса угла С, то единственным корнем уравнения (1’) является x=CD*.
в том, и только том случае, когда точка D лежит на отрезке АВ. Следовательно, поскольку CD – биссектриса угла С, то единственным корнем уравнения (1’) является x=CD*.
Длина биссектрисы треугольника АВС, проведенной из вершины С, может быть вычислена по формуле Симпсона:
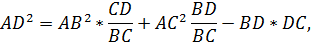
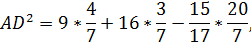
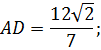
И это единственный корень уравнения (1’).
Ответ. 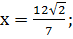
Заключение.
И так, в своей работе я выполнила следующее:
- на примерах рассмотрела геометрический способ решения алгебраических уравнений и систем;
- проанализировала рациональность применения этого метода на конкретных примерах;
- рассмотрела применение теоремы косинусов для решения некоторых видов иррациональных уравнений.
Я думаю, что основной трудностью при применении геометрического способа является неочевидность. Все уравнения и системы, рассмотренные мной в работе (кроме последней), имеют стандартное алгебраическое решение. Поэтому рациональность геометрического способа – вопрос спорный. Однако, при решении некоторых систем этот способ – единственно возможный, кроме того, он еще и красив!
При решении системы из примера 1 геометрический способ становится эффективным, если в условии не требуется находить решения системы, а, например, значения x + z, y(x +z) и так далее. Тогда из геометрического чертежа ответы на эти вопросы становятся очевидными.
Чем большим количеством способов мы можем решить то или иное уравнение, тем скорее мы научимся рациональности в своих рассуждениях и действиях. А для этого надо решать! Решать больше, учиться находить различные пути. Ведь жизнь предполагает многовариантность!
Литература.
1. Потоскуев Е. В. Векторы и координаты как аппарат решения геометрических задач. –М., Дрофа,2008.
2. Попов В. А. Иррациональные уравнения, неравенства и теорема косинусов. – «Математика в школе», №6- 1998, с. 52.
3. Генкин Г. З. Геометрические решения алгебраических задач. - «Математика в школе», №7- 2001, с. 61.
4. Мигина А. Решение уравнений с применением оригинальных приемов. – Газета «Математика», №37 – 2001, с. 26.
5. Кравцев С. Ю., Макаров Ю. И., Максимов М. И. и др. Методы решения задач по алгебре: от простых до самых сложных. – М.: Экзамен, 2001.
Приложение 1.
· Вектор– это отрезок, для которого указано, какой из его концов считается началом, а какой концом.
· Векторы называются коллинеарными, если они лежат, либо на одной прямой, либо на параллельных прямых.
· Векторы называются равными, если они сонаправлены и их длины равны.
· Скалярное произведение векторов:
Скалярным произведением векторов называется произведение их длин на косинус угла между ними.
Скалярное произведение векторов 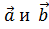 обозначается так:
обозначается так: 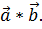 Или
Или 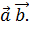
По определению:
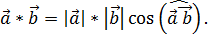
· Скалярное произведение векторов 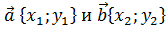 выражается формулой
выражается формулой
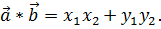
· Расстояние между точками А и В.
Расстояние между точками А(х1;у1) и В(х2;у2) выражается формулой:
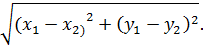
· Теорема косинусов:
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
· 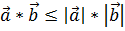 , так как косинус угла между векторами
, так как косинус угла между векторами 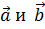 меньше или равен единице.
меньше или равен единице.
Приложение 2.
Пример №1.Докажите, что для всех 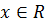 выполняется неравенство:
выполняется неравенство:
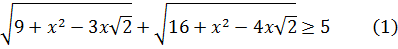
Решение.
Заметим, что если 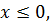 то
то
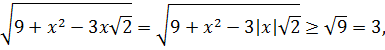
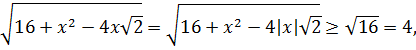
Поэтому значение левой части неравенства (1) в этом случае не меньше, чем 3+4=7.
Чтобы убедиться в истинности неравенства (1) при 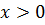 , рассмотрим треугольник ACD, в котором АС=3, CD=x, a угол ACD =
, рассмотрим треугольник ACD, в котором АС=3, CD=x, a угол ACD = 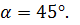 В силу теоремы косинусов имеем:
В силу теоремы косинусов имеем:
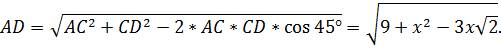
Аналогично, если СВ=4, CD=x, а угол BCD = 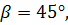 поэтому
поэтому 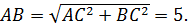 Следовательно, с помощью неравенства треугольника получаем:
Следовательно, с помощью неравенства треугольника получаем:
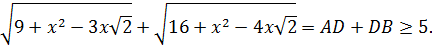
Ответ: в основу неравенства (1) положен египетский треугольник, т.е. прямоугольный треугольник со сторонами 3,4,5.
Другие истинные неравенства можно получить, пользуясь пифагоровыми тройками чисел, например 5,12,13 и 8,15,17,
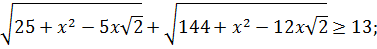
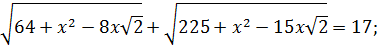
пользуясь общим неравенством:
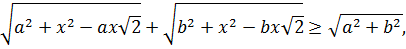
которое выполняется для любых 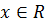 и
и 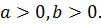
На следующем этапе опять действует аналогия. Мы видим, что метод рассмотрения прямоугольного треугольника со сторонами 3,4,5 и прямым углом, который разбивается на два угла 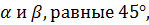 оказывается столь же эффективным, если
оказывается столь же эффективным, если 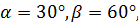 для этих значений так же легко составить неравенство:
для этих значений так же легко составить неравенство:
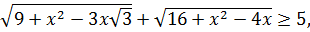 верное при любых
верное при любых 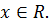
Все рассмотренные случаи приводят к общему неравенству
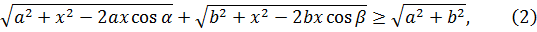
которое справедливо для 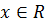 и
и 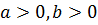 и
и 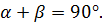
Дальнейшие вариации неравенства (2) становятся возможными, если отказаться от условия 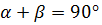 и принять, что в треугольнике АВС АС =1б СВ=ВА и
и принять, что в треугольнике АВС АС =1б СВ=ВА и 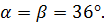
Такое значение угла удобно тем, что его синус и косинус выражаются алгебраическими числами. Так, 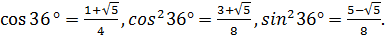
Тогда 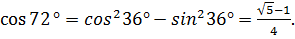 Поскольку
Поскольку 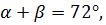 применим теорему косинусов для вычисления длин сторон АВ и СВ( обозначим их через у):
применим теорему косинусов для вычисления длин сторон АВ и СВ( обозначим их через у):
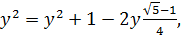 т.е.
т.е. 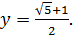
Теперь теорема косинусов «работает» в треугольниках CBD и CDA. Обозначив их общую сторону через х, из треугольника CBD получаем:
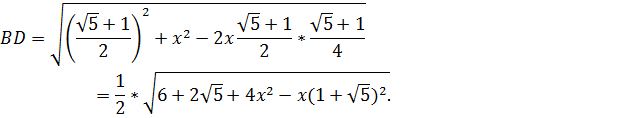
Из треугольника CDA:
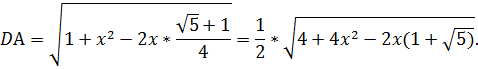
Как и в предыдущих случаях воспользуемся неравенством треугольника 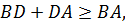 переписав его в следующем виде:
переписав его в следующем виде:
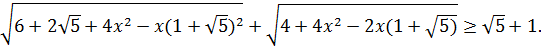
Это неравенство справедливо для всех 
В общем случае для всех положительных чисел х, а, в и углов α и β, таких, что α+β≥90º, выполняется:
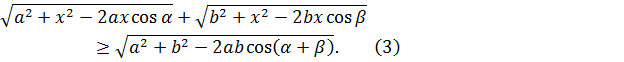
Анализируя путь от неравенства (1) к неравенству (3), замечаем, что до сих пор мы имели одну независимую переменную х (в связи с этим в доказательствах были использованы два угла α и β). Снятие этого ограничения открывает широкий простор для новых задач.
Пример №2.
Докажите, что для всех 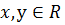 выполняется неравенство:
выполняется неравенство:
Решение.
Заметим, что при любых  выполняется равенство:
выполняется равенство:
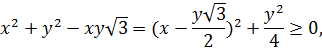
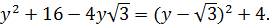
Следовательно, значение левой части исходного неравенства
1) при 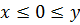 не меньше, чем
не меньше, чем
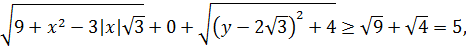
2) при 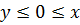 значение левой части доказываемого неравенства не меньше, чем
значение левой части доказываемого неравенства не меньше, чем
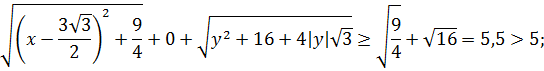
3)при 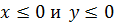 значение левой части оказывается не меньше , чем
значение левой части оказывается не меньше , чем
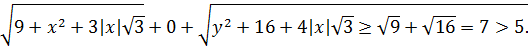
Случаи x>0, y>0 рассмотрим с помощью теоремы косинусов, применяемой а треугольнике АВС, у которого АС=3, ВС=4 и угол АСВ=90º. Тогда АВ=5. На лучах, делящих угол АСВ на три равные части, выбираем точки D1 и D2 так, чтобы CD1=x, CD2=y. По теореме косинусов из треугольников ACD1, D1CD2, D2CB имеем:
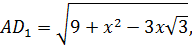
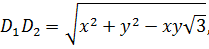
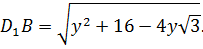
Так как периметр ломаной линии всегда не меньше длины отрезка, соединяющего начало и конец этой ломаной, то
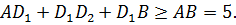
Отсюда в силу трех предыдущих неравенств следует неравенство (4) при x>0 и y>0.
Итак, неравенство (4) доказано для любых действительных значений х и у.
Покажем ещё два неравенства, которые можно получить по аналогии с неравенством (4). Так,
Треугольник АВС, у которого катет АС=25, катет ВС=37, а прямой угол С разделен на три угла α=15º, β=30º, ɣ=45º, можно доказать неравенство
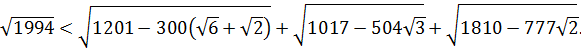
Продемонстрируем теперь преимущества применения теоремы косинусов к некоторым иррациональным уравнениям. Рассмотрим уравнение, которое получается из приведенных ниже неравенств заменой знака «≥» на знак «=». Ясно, что это иррациональное уравнение весьма сложно решить традиционными алгебраическими средствами. Метод же, изложенный выше для доказательства неравенств, прост и нагляден. Его теоретическую часть следует только дополнить таким утверждением: если длина ломаной равна длине стягивающего ее отрезка АВ, то все вершины этой ломаной лежат на отрезке АВ, т.е. ломаная фактически вырождается в отрезок АВ.
Описанный ниже метод хорош ещё и тем, что вычисление корней уравнения, как правило, позволяет свести к стандартным геометрическим вычислениям длины биссектрисы треугольника.
