Формула мощности объединения двух множеств A и B

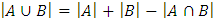
Формула мощности объединения трех множеств A, B и С

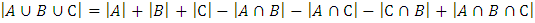
Примеры решения

Задание 1

Пусть множество А – это область определения функции

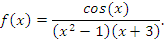
Множество В – это область определения функции

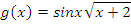
Найти и изобразить на числовой прямой множества

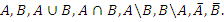
Решение

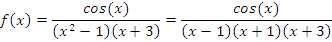
Функция не определена при 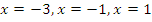. Следовательно,

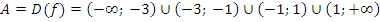
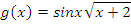
Функция определена при 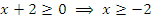. Следовательно,

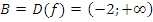
Тогда

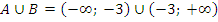
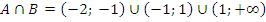
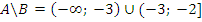
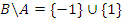
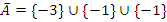
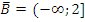
Задание 2

Среди 160 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 45 абитуриентов, по физике – 39, по русскому языку – 44, по математике или физике – 78, по математике или русскому языку – 72, по физике и русскому языку – 14, по всем трём предметам – 6.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

Решение

Пусть множество А – абитуриенты, получившие «пятерки» на экзамене по математике, множество В – абитуриенты, получившие отличную оценку на вступительном экзамене по физике, множество С – те, кто сдал на «отлично» русский язык.

U – это универсальное множество, то есть все абитуриенты.

Тогда по условию задачи

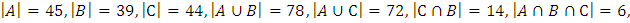
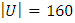
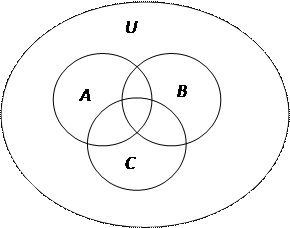
Пусть D – множество абитуриентов, которые получили хотя бы одну пятёрку.

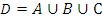
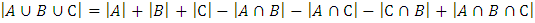
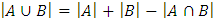
Задания для самостоятельного решения

Задание 1

Пусть множество А – это область определения функции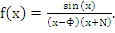

Множество В – это область определения функции

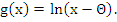
Найти и изобразить на числовой прямой множества

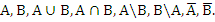
В задание используются следующие обозначения:

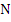– количество букв в Вашем полном имени;

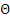– количество букв в Вашем отчестве;

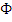– количество букв в Вашей фамилии.

Задание 2

1. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

2. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

3. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике и физике – 10, по математике и русскому языку – 14, по физике или русскому языку – 66, по всем трём предметам – 4.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

4. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

5. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

6. Среди 155 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 73, по математике или русскому языку – 72, по физике и русскому языку – 13, по всем трём предметам – 4.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

7. Среди 160 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

8. Среди 155 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 47 абитуриентов, по физике – 36, по русскому языку – 42, по математике или физике – 12, по математике или русскому языку – 76, по физике и русскому языку – 14, по всем трём предметам – 5.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

9. Среди 170 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 52 абитуриента, по физике – 38, по русскому языку – 41, по математике или физике – 75, по математике и русскому языку – 14, по физике или русскому языку – 66, по всем трём предметам – 7.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

10. Среди 150 абитуриентов, выдержавших приёмные экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 абитуриентов, по физике – 37, по русскому языку – 42, по математике или физике – 75, по математике или русскому языку – 76, по физике или русскому языку – 66, по всем трём предметам – 4.

Сколько абитуриентов получили хотя бы одну пятёрку? Сколько абитуриентов не получили ни одной пятёрки? Только одну пятерку?

Контрольные вопросы

1. Что такое множество?

2. Какие способ задания множества вы знаете?

3. Что такое мощность множества?

4. Какие операции над множествами вы знаете?

5. Напишите формулу мощности объединения четырех множеств и проиллюстрируйте ее диаграммой вена.