Полярная система координат
Говорят, что на плоскости введена полярная система координат, если заданы:
1) некоторая точка 0, называемая полюсом;
2) некоторый луч, исходящий из точки 0 и называемый полярной осью.
Полярными координатами точки M называются два числа: полярный радиус 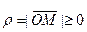 и полярный угол
и полярный угол 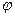 - угол между полярной осью и вектором
- угол между полярной осью и вектором 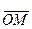 .
.
Пусть на плоскости введены декартова и полярная системы координат, причем начало декартовой системы совпадает с полюсом, а полярная ось - с положительной полуосью абсцисс. Тогда прямоугольные координаты x, y точки М и ее полярные координаты ρ, φ связаны следующими формулами:
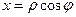 ,
, 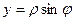
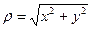 ,
, 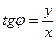
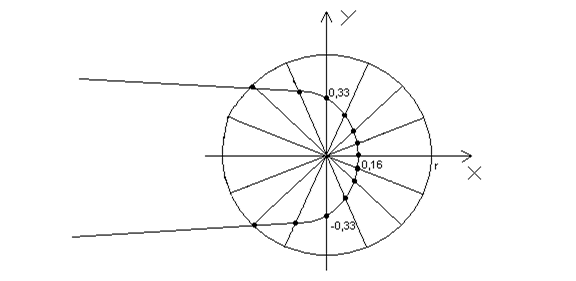
Задание 4. Линия задана уравнением 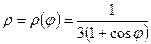 в полярной системе координат. Требуется:
в полярной системе координат. Требуется:
1. Построить линию по точкам, придавая φ значения от 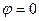 до
до 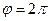 через промежуток
через промежуток 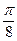 .
.
2. Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.
3. По уравнению в декартовой прямоугольной системе координат определить тип линии.
Решение.
1) Совместим декартову и полярную системы координат и рассмотрим окружность произвольного, достаточно большого радиуса 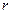 с центром в полюсе. Построим радиусы, образующие углы
с центром в полюсе. Построим радиусы, образующие углы 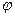 с полярной осью, где
с полярной осью, где 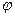 принимает значения от
принимает значения от 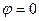 до
до 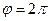 с шагом
с шагом 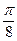 . Вычислим косинусы этих углов и по этим значениям найдем
. Вычислим косинусы этих углов и по этим значениям найдем 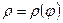 . Результаты вычислений занесем в таблицу:
. Результаты вычислений занесем в таблицу:
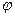 | 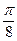 | 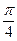 | 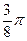 | 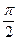 | 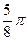 | 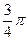 | 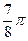 | 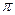 | 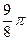 | 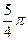 | 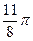 | 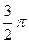 | 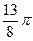 | 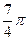 | 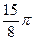 | 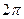 | |
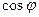 | 0,92 | 0,7 | 0,38 | -0,38 | -0,7 | -0,92 | -1 | -0,92 | -0,7 | -0,38 | 0,38 | 0,7 | 0,92 | ||||
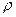 | 0,16 | 0,17 | 0,19 | 0,24 | 0,33 | 0,53 | 1,11 | 4,16 | ∞ | 4,16 | 1,11 | 0,53 | 0,33 | 0,24 | 0,19 | 0,17 | 0,16 |
Построим точки ( 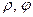 ) и по полученным точкам построим искомую линию:
) и по полученным точкам построим искомую линию:
2) Найдем уравнение данной линии в декартовой системе координат. Для этого воспользуемся формулами:
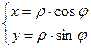 .
.
Отсюда 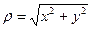 ,
, 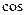
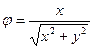 .
.
Тогда имеем:
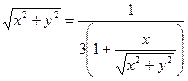
или после упрощения
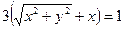 .
.
3) Чтобы определить тип линии, определяемой полученным уравнением,
преобразуем его к каноническому виду:
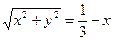
или
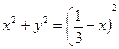 .
.
Окончательно получим:
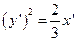 ,
,
где 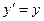 ,
, 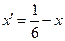 . Таким образом, данное уравнение определяет параболу.
. Таким образом, данное уравнение определяет параболу.
Комплексные числа
Выражение вида 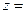
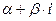 , где
, где 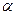 и
и 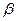 - вещественные числа,
- вещественные числа, 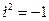 , называется комплексным числом (в алгебраической форме).
, называется комплексным числом (в алгебраической форме).
Комплексное число 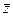 =
= 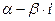 называется комплексно-сопряженным числом к комплексному числу
называется комплексно-сопряженным числом к комплексному числу 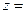
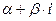 .
.
Действия над комплексными числами. Пусть даны два комплексных числа: 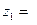
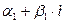 и
и 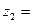
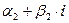 . Тогда
. Тогда
1) 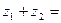
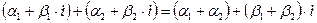
2) 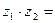
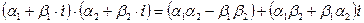
3) 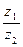 =
= 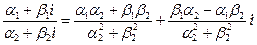 .
.
Для любого комплексного числа 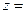
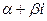 имеем:
имеем: 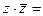
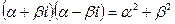
Величина 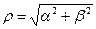 называется модулем комплексного числа. Угол
называется модулем комплексного числа. Угол 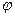 , определяемый равенствами
, определяемый равенствами 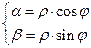 ,
, 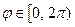 , называется аргументом комплексного числа.
, называется аргументом комплексного числа.
Любое комплексное число можно записать в тригонометрической форме:
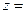
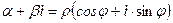 ,
,
где 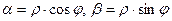 .
.
Для выполнения действий возведения комплексного числа в натуральную степень и извлечения корня с натуральным показателем используются формулы Муавра:
1) 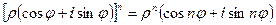 ;
;
2) 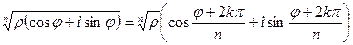 ,
, 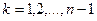 .
.
Задание 5 Дано комплексное число 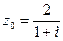 . Требуется:
. Требуется:
1) записать данное число в алгебраической и тригонометрической формах;
2) найти все корни уравнения 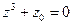 .
.
Решение 1) Приведем комплексное число  к алгебраической форме:
к алгебраической форме: 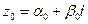 .
.
Для этого умножим числитель и знаменатель дроби  на число
на число 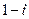 , комплексно-сопряженное знаменателю. Получим:
, комплексно-сопряженное знаменателю. Получим:
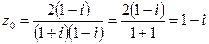 .
.
Это и есть алгебраическая формакомплексногочисла  , где
, где 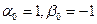 .
.
Теперь приведем комплексное число 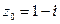 к тригонометрическому виду:
к тригонометрическому виду: 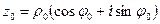 , где
, где 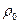 - модуль комплексного числа
- модуль комплексного числа  ,
, 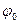 - аргумент этого числа.
- аргумент этого числа.
Для этого найдем 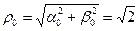 . Для нахождения
. Для нахождения 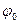 имеем систему:
имеем систему:
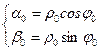
или
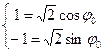
и тогда 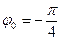 . Следовательно, тригонометрическая форма комплексного числа
. Следовательно, тригонометрическая форма комплексного числа 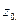 имеет вид:
имеет вид:
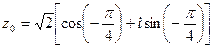 .
.
3) Найдем теперь все корни уравнения 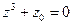 , откуда
, откуда 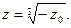 Тригонометрическая форма комплексного числа -
Тригонометрическая форма комплексного числа -  имеет вид:
имеет вид: 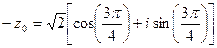 .
.
По второй из формул Муавра получаем:
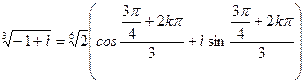 , где
, где 
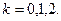
Тогда корни уравнения имеют вид:
1. При 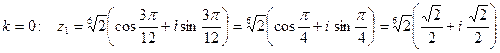 ;
;
2. При 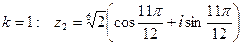 ;
;
3. При 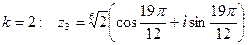 .
.

