Цилиндрические и сферические координаты в пространстве

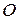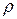Введем полярные координаты на плоскости. Для этого выберем на плоскости некоторую точку , которую будем называть полюсом, и некоторый выходящий из нее луч, который мы будем называть полярной осью. Кроме того, укажем единицу масштаба. Полярными координатами точки называются числа и 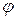, первое из которых 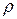равно расстоянию от этой точки до полюса и называется полярным радиусом, а второе 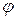– равно углу, на который нужно повернуть против часовой стрелки полярную ось, чтобы совместить ее с лучом 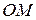, и называется полярным углом. Упорядоченная пара 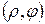однозначно определяет положение точки на плоскости. Точку с указаными полярными координатами обозначают: .

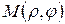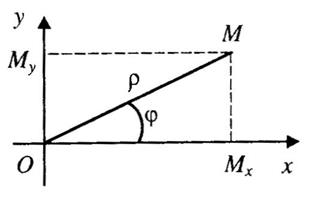При совмещении на плоскости декартовой и полярной систем координат полюс совмещают с началом декартовой системы, а направление полярной оси выбирают таким же, как и положительное направление оси абсцисс. При этом очевидны формулы перехода от декартовой к полярной системе координат:

,

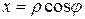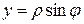
(см. рис). Кроме того, справедливы формулы перехода от полярной к декартовой системе:

,

.

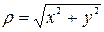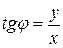Введем цилиндрические координаты в пространстве. Для этого зафиксируем плоскость 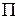, в которой вводится полярная система координат. Проводим ось 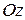, проходящую через полюс перпендикулярно к выбранной плоскости, и выбираем на оси в качестве начала координат полюс. Кроме того, укажем единицу масштаба.

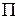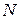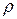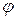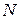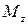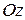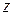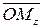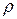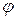Рассмотрим произвольную точку в пространстве. Спроектируем эту точку на плоскость . Получим точку . Пусть и - полярные координаты точки . Также найдем точку - проекцию точки на ось . Пусть - величина направленного отрезка . Цилиндрическими координатами точки называются числа , и 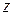. Действительно, упорядоченная тройка 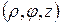однозначно определяет положение точки в простанстве. Точку с указаными цилиндрическими координатами обозначают: .

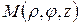Название «цилиндрические координаты» связано с тем, что координатная поверхность 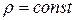является цилиндром.

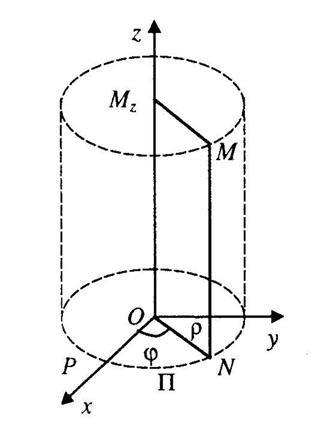При совмещении в пространстве декартовой и цилиндрической систем координат поступают следующим образом: полярную систему координат плоскости 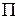совмещают, как указано выше, с декартовой системой плоскости 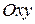, а также совмещают оси 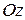. При этом очевидны формулы перехода от декартовой к цилиндрической системе координат:

,

,

,

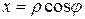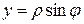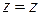а также формулы обратного перехода:

,

,

.

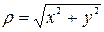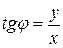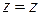Введем сферические координаты в пространстве. Для этого зафиксируем плоскость 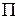, в которой вводится полярная система координат. Проводим ось 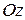, проходящую через полюс перпендикулярно к выбранной плоскости, и выбираем на оси в качестве начала координат полюс. Кроме того, укажем единицу масштаба.

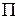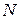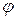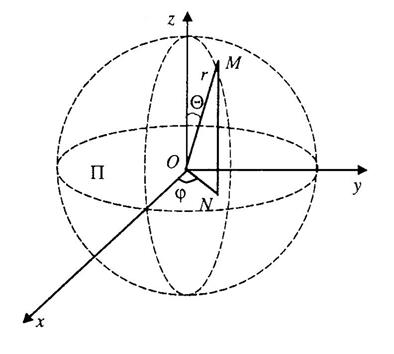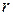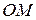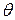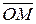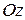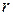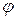Рассмотрим произвольную точку в пространстве. Спроектируем эту точку на плоскость . Получим точку . Пусть - полярный угол этой точки, - длина отрезка , а - угол между направленным отрезком и осью . Сферическими координатами точки называются числа , и 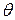. Действительно, упорядоченная тройка 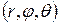однозначно определяет положение точки в простанстве. Точку с указаными цилиндрическими координатами обозначают: 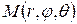. При этом координаты 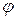и 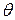называются долготой и широтой соответственно.

Название «сферические координаты» связано с тем, что координатная поверхность 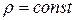является сферой.

При совмещении в пространстве декартовой и сферической систем координат поступают так же, как и в случае цилиндрической системы. Пусть 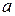- длина отрезка 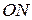. Тогда из рисунка видно, что

.

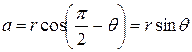Следовательно, формулы перехода от декартовой к цилиндрической системе координат имеют вид:

,

,

.

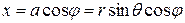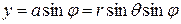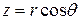Очевидны также формулы обратного перехода:

,

,

.
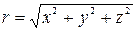
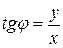
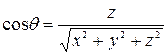