Выполнить действия в алгебраической форме. Результаты записать в тригонометрической и показательной формах
| 1. | 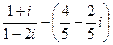 |
| 2. | 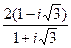 |
| 3. | 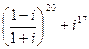 |
| 4. | 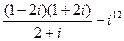 |
| 5. |  |
| 6. | 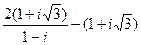 |
| 7. | 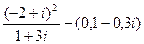 |
| 8. |  |
| 9. | 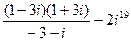 |
| 10. | 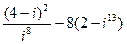 |
II. Задание.
Решите систему трех линейных уравнений с тремя неизвестными методом Гаусса; по формулам Крамера и матричным методом.
| 11. |  |
| 12. | 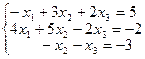 |
| 13. | 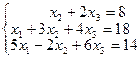 |
| 14. | 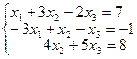 |
| 15. |  |
| 16. |  |
| 17. | 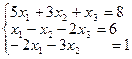 |
| 18. |  |
| 19. |  |
| 20. | 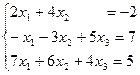 |
III. Задание
21. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(3; –1; 2), B(1; 1; 1), C(–5; 3; 1).
22. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1).
23. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(4; –2; 5), B(2; 2; 1), C(3; 6; 1).
24. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(–3; 7; 1), B(1; 5; 3), C(2; –7; 3).
25. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(2; 3; –6), B(5; –1; 6), C(4; 1; 3).
26. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(–1; 5; 4), B(5; –4; 2), C(1; 3; 3).
27. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(5; –2; 3), B(4; 6; –1), C(1; 2; 1).
28. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(8; –3; –1), B(4; –1; 3), C(–1; 3; 1).
29. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(–6; 1; 4), B(8; 3; –1), C(2; 5; 3).
30. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
Найти:
а) координаты векторов  и
и  ;
;
б) скалярное произведение векторов  и
и  ;
;
в) угол между векторами  и
и  ;
;
A(–2; –4; 1), B(4; 5; 3), C(1; 8; 5).
IV. Задание.
Вычислить следующие пределы:
31. а) 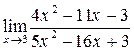 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
32. а) 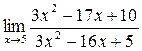 ; б)
; б)  ; в)
; в) 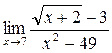 ; г)
; г) 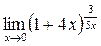 .
.
33. а) 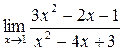 ; б)
; б) 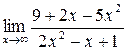 ; в)
; в) 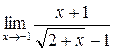 ; г)
; г)  .
.
34. а)  ; б)
; б) 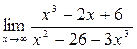 ; в)
; в) 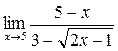 ; г)
; г) 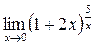 .
.
35. а)  ; б)
; б) 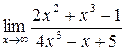 ; в)
; в) 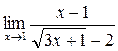 ;..г)
;..г) 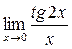 .
.
36. а) 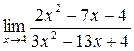 ; б)
; б) 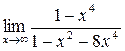 ; в)
; в)  ; г)
; г) 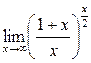 .
.
37. а) 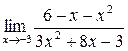 ; б)
; б) 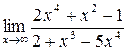 ; в)
; в) 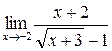 ; г)
; г) 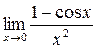 .
.
38. а) 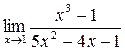 ; б)
; б) 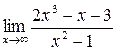 ; в)
; в) 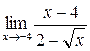 ; г)
; г) 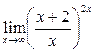 .
.
39. а) 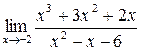 ; б)
; б)  ; в)
; в) 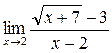 ; г)
; г)  .
.
40. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
V. Задание.
Найти производные функций при заданном значении аргумента
| 41. | а) 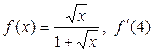 ; б) ; б) 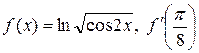 . . |
| 42. | а) 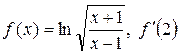 ; б) ; б)  . . |
| 43. | а) 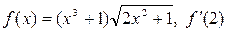 ; б) ; б) 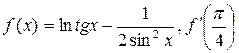 . . |
| 44. | а)  ; б) ; б) 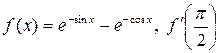 . . |
| 45. | а) 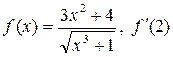 ; б) ; б) 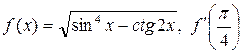 . . |
| 46. | а)  ; б) ; б)   . . |
| 47. | а) 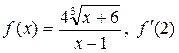 ; б) ; б) 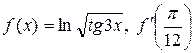 . . |
| 48. | а) 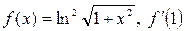 ; б) ; б) 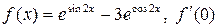 . . |
| 49. | а)  ; б) ; б)  . . |
| 50. | а)  ; б) ; б)  . . |
ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ № 2
I. Задание.
Исследовать данные функции методами дифференциального исчисления и построить их графики. При исследовании функции следует найти ее интервалы возрастания и убывания и точки экстремума, интервалы выпуклости и вогнутости и точки перегиба графика функции.
| 1. | 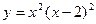 |
| 2. | 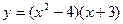 |
| 3. |  |
| 4. | 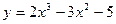 |
| 5. | 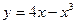 |
| 6. |  |
| 7. | 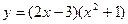 |
| 8. |  |
| 9. |  |
| 10. | 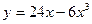 |
II. Задание.
Вычислить определенный интеграл:
| 11. | а) 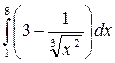 ; б) ; б) 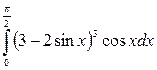 . . |
| 12. | а) 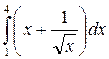 ; б) ; б)  . . |
| 13. | а) 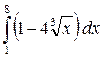 ; б) ; б) 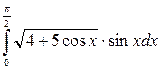 . . |
| 14. | а) 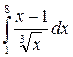 ; б) ; б)  . . |
| 15. | а) 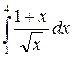 ; б) ; б)  . . |
| 16. | а) 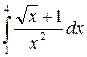 ; б) ; б) 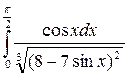 . . |
| 17. | а)  ; б) ; б) 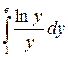 . . |
| 18. | а)  ; б) ; б) 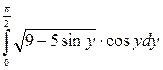 . . |
| 19. | а) 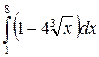 ; б) ; б) 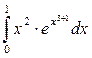 . . |
| 20. | а) 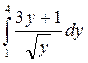 ; б) ; б)  . . |
III. Задание.
