Глава 8. Дифференциальные уравнения

Основные понятия и определения

Определение

Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции.

Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным, если от нескольких – то уравнением в частных производных.

Простейший пример дифференциального уравнения дает задача о нахождении первообразной 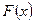для заданной функции 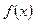, поскольку ее можно рассматривать как задачу о нахождении функции 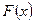, удовлетворяющей уравнению .

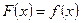В общем случае дифференциальное уравнение можно записать в виде

,

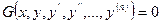(8.1.1)

где G – некоторая функция от n+2 переменных, при этом порядок 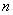старшей производной, входящей в запись уравнения, называется порядком дифференциального уравнения.

Основной задачей теории обыкновенных дифференциальных уравнений является нахождение функций, представляющих собой решения этих уравнений.

Определение

Решением дифференциального уравнения (8.1.1) называется такая функция y=y(x), которая при подстановке в это уравнение обращает его в тождество.

Например, функция y=sin(x) является решением уравнения 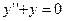, так как 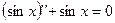для всех x.

Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.

Пример

Решить уравнение .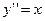

Решение

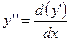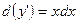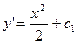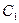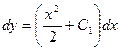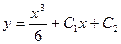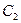Поскольку , то исходное уравнение равносильно следующему равенству дифференциалов . Выполняя по членное интегрирование получаем , где – произвольная постоянная. Вновь записывая производную как отношение двух дифференциалов, приходим к равенству , интегрируя почленно окончательно получаем , где – произвольная постоянная.

Отметим, что без дополнительных предположений решение данного уравнения принципиально неоднозначно. Другими словами, дифференциальное уравнение задает семейство интегральных кривых на плоскости. Для выделения однозначно определенной интегральной кривой (решения) в нашем случае достаточно указать точку плоскости, через которую проходит искомая интегральная кривая, и направление, в котором она проходит через эту точку.

Дополнительные условия такого рода обычно называют начальными условиями, поскольку часто дифференциальные уравнения используются для описания динамических процессов – процессов, происходящих во времени.

Для выделения однозначно определенного решения дифференциального уравнения 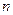–го порядка следует, вообще говоря, дополнительно задать 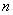начальных условий.

Определение

Общим решением дифференциального уравнения (8.1.1) 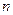–го порядка называется такое его решение

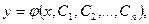(8.1.2)

которое является функцией переменно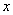й и 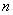произвольных независимых постоянных.

Частным решением дифференциального уравнения называется решение, получаемое из общего решения при заданных конкретных значениях констант.

В нашем примере 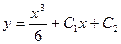– общее решение, 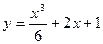– частное решение дифференциального уравнения .

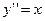Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые заданного семейства (8.1.2), нужно продифференцировать равенство 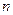раз, а затем из полученных равенств исключить константы.

Пример

Составить дифференциальное уравнение семейства кривых .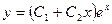

Решение

Дифференцируя заданную функцию, находим 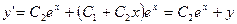, 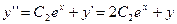. Исключая из этих двух равенств 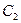, приходим к уравнению .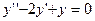