Определение. Частные производные вида и т.д. называются смешанными производными

Теорема. Если функция f(x, y) и ее частные производные 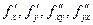определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение:

.

Т.е. частные производные высших порядков не зависят от порядка дифференцирования.

Аналогично определяются дифференциалы высших порядков.

…………………

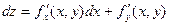
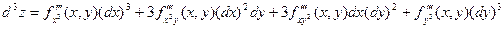
Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего с скобках выражения.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая находит все производные до второго порядка включительно для функции двух переменных.

Для запуска программы дважды щелкните на значке

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Экстремум функции нескольких переменных.

Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

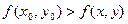
то точка М₀ называется точкой максимума.

Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

то точка М₀ называется точкой минимума.