Производная и дифференциал 2 страница
38. Производные высших порядков. Правила вычисления, правило Лейбница. Пусть функция y=f(x) дифференцируема на некотором отрезке [a; b]. Значение производной f'(x), вообще говоря, зависит от x, т.е. производная f'(x) представляет собой тоже функцию переменной x. Пусть эта функция также имеет производную. Дифференцируя ее, получим так называемую вторую производную от функции f(x). Производная от первой производной называется производной второго порядка или второй производной от данной функции y=f(x) и обозначается y''или f''(x). Итак, y'' = (y')'. Например, если у = х5, то y'= 5x4, а y''= 20x4. Аналогично, в свою очередь, производную второго порядка тоже можно дифференцировать. Производная от второй производной называется производной третьего порядка или третьей производной и обозначается y'''или f'''(x). Вообще, производной n-го порядка от функции f(x) называется производная (первая) от производной (n – 1)-го порядка и обозначается символом y(n) или f(n)(x): y(n) = (y(n-1))'.  Таким образом, для нахождения производной высшего порядка от данной функции последовательно находят все ее производные низших порядков. Таким образом, для нахождения производной высшего порядка от данной функции последовательно находят все ее производные низших порядков.  | 40. Дифференцирование параметрически заданных функций. | 41. Дифференциалы высших порядков. Нарушение инвариантности формы. Пусть имеем функцию y=f(x), где x – независимая переменная. Тогда дифференциал этой функции dy=f'(x)dx также зависит от переменной x, причем от x зависит только первый сомножитель f'(x) , а dx = Δx от x не зависит (приращение в данной точке x можно выбирать независимо от этой точки). Рассматривая dy как функцию x, мы можем найти дифференциал этой функции. Дифференциал от дифференциала данной функции y=f(x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y: d(dy)=d2y. Найдем выражение второго дифференциала. Т.к. dx от x не зависит, то при нахождении производной его можно считать постоянным, поэтому d2y=d(dy) =d[f'(x)dx)] = [f'(x)dx]'dx=f''(x)dx·dx=f''(x)(dx)2. Принято записывать (dx)2 = dx2. Итак, d2у= f''(x)dx2. Аналогично третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала: d3y=d(d2y)=[f ''(x)dx2]'dx=f '''(x)dx3. Вообще дифференциалом n-го порядка называется первый дифференциал от дифференциала (n – 1)-го порядка: dn(y)=d(dn-1y) dny=f(n)(x)dxn Отсюда, пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка: 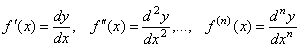 Неинвариантность дифференциалов высшего порядка При Неинвариантность дифференциалов высшего порядка При 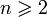 , , 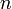 -й дифференциал не инвариантен (в отличие от инвариантности первого дифференциала), то есть выражение -й дифференциал не инвариантен (в отличие от инвариантности первого дифференциала), то есть выражение 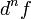 зависит, вообще говоря, от того, рассматривается ли переменная зависит, вообще говоря, от того, рассматривается ли переменная 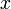 как независимая, либо как некоторая промежуточная функция другого переменного, например, x = φ(t). Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример. При n = 2 и как независимая, либо как некоторая промежуточная функция другого переменного, например, x = φ(t). Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример. При n = 2 и 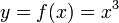 : если : если 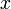 — независимая переменная, то — независимая переменная, то 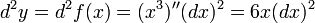 если если 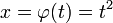 и и 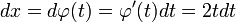 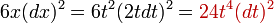 при этом, при этом, 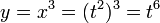 и и 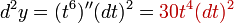 С учётом зависимости С учётом зависимости 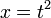 , уже второй дифференциал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифференциалы порядков 3 и выше. , уже второй дифференциал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифференциалы порядков 3 и выше. |
42. Теорема Ферма   | 43. Теорема Ролля | 44. Формула конечных приращений Лагранжа. Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка 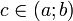 , что , что 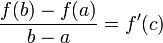 . Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка. Механическое истолкование: Пусть f(t) — расстояние точки в момент t от начального положения. Тогда f(b) − f(a) есть путь, пройденный с момента t = a до момента t = b, отношение . Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка. Механическое истолкование: Пусть f(t) — расстояние точки в момент t от начального положения. Тогда f(b) − f(a) есть путь, пройденный с момента t = a до момента t = b, отношение 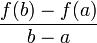 — средняя скорость за этот промежуток. Доказательство Для функции одной переменной: Введем функцию — средняя скорость за этот промежуток. Доказательство Для функции одной переменной: Введем функцию 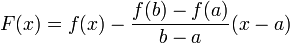 . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю: . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю: 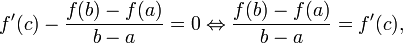 что и требовалось доказать. что и требовалось доказать. |
45. Теорема Коши. Пусть даны две функции 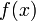 и и  такие, что: такие, что: 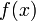 и и  определены и непрерывны на отрезке определены и непрерывны на отрезке 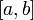 ; производные ; производные 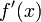 и и 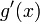 конечны на интервале конечны на интервале 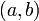 производные производные 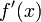 и и 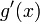 не обращаются в нуль одновременно на интервале не обращаются в нуль одновременно на интервале 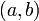 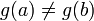 ; тогда ; тогда 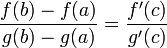 , где , где 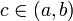 Доказательство Для доказательства введём функцию Доказательство Для доказательства введём функцию 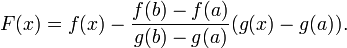 Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а 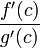 равна как раз необходимому числу. равна как раз необходимому числу. | 46. Правило Лопиталя раскрытия неопределенности 0/0 Точная формулировка Условия: 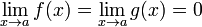 или или 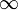 ; ; 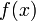 и и  дифференцируемы в проколотой окрестности дифференцируемы в проколотой окрестности 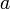 ; ; 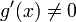 в проколотой окрестности в проколотой окрестности 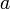 ; существует ; существует 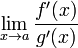 , тогда существует , тогда существует 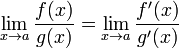 . Пределы также могут быть односторонними. Отношение бесконечно малых Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида . Пределы также могут быть односторонними. Отношение бесконечно малых Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида  ). Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f(a) = g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку ). Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образом их доопределить в этой точке: пусть f(a) = g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку 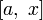 теорему Коши. По этой теореме получим: теорему Коши. По этой теореме получим: 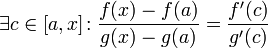 , но f(a) = g(a) = 0, поэтому , но f(a) = g(a) = 0, поэтому 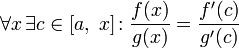 . Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим: . Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим: 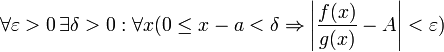 для конечного предела и для конечного предела и 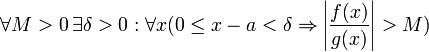 для бесконечного, что является определением предела отношения функций. для бесконечного, что является определением предела отношения функций. | 47. Правило Лопиталя для раскрытия неопределенности ∞/∞ Точная формулировка Условия: 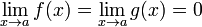 или или 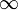 ; ; 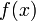 и и  дифференцируемы в проколотой окрестности дифференцируемы в проколотой окрестности 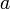 ; ; 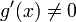 в проколотой окрестности в проколотой окрестности 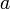 ; существует ; существует 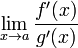 , , 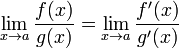 Докажем теорему для неопределённостей вида Докажем теорему для неопределённостей вида  . Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие: . Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие: 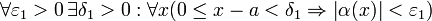 . Зафиксируем t из отрезка . Зафиксируем t из отрезка 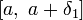 и применим теорему Коши ко всем x из отрезка и применим теорему Коши ко всем x из отрезка 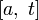 : : 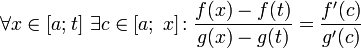 , что можно привести к следующему виду: , что можно привести к следующему виду: 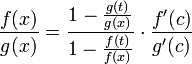 . Для x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f(t) и g(t) — константы, а f(x) и g(x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение ε, что и в определении для α: . Для x, достаточно близких к a, выражение имеет смысл; предел первого множителя правой части равен единице (так как f(t) и g(t) — константы, а f(x) и g(x) стремятся к бесконечности). Значит, этот множитель равен 1 + β, где β — бесконечно малая функция при стремлении x к a справа. Выпишем определение этого факта, используя то же значение ε, что и в определении для α: 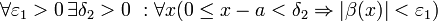 . Получили, что отношение функций представимо в виде (1 + β)(A + α), и . Получили, что отношение функций представимо в виде (1 + β)(A + α), и 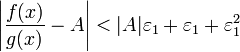 . По любому данному ε можно найти такое ε1, чтобы модуль разности отношения функций и A был меньше ε, значит, предел отношения функций действительно равен A. Если же предел A бесконечен (допустим, он равен плюс бесконечности), то . По любому данному ε можно найти такое ε1, чтобы модуль разности отношения функций и A был меньше ε, значит, предел отношения функций действительно равен A. Если же предел A бесконечен (допустим, он равен плюс бесконечности), то 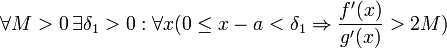 . В определении β будем брать . В определении β будем брать 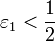 ; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда ; первый множитель правой части будет больше 1/2 при x, достаточно близких к a, а тогда 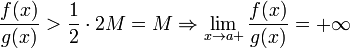 . . |
 48. Локальная формула Тейлора. Остаточный член в форме Пеано. Пусть 48. Локальная формула Тейлора. Остаточный член в форме Пеано. Пусть 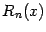 -- остаток в формуле Тейлора для функции -- остаток в формуле Тейлора для функции  в точке в точке  , и функция , и функция  имеет непрерывную имеет непрерывную  -ю производную. Тогда -ю производную. Тогда 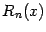 -- бесконечно малая величина того же или большего порядка малости, как -- бесконечно малая величина того же или большего порядка малости, как 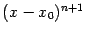 , при , при 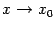 . (Остаточный член . (Остаточный член 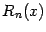 , о котором известны эти сведения о порядке малости, называется остаточным членом в форме Пеано.) Остаточный член в форме Пеано: В форме Пеано: , о котором известны эти сведения о порядке малости, называется остаточным членом в форме Пеано.) Остаточный член в форме Пеано: В форме Пеано: 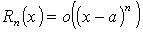 при при 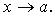 Доказательство. Утверждение теоремы означает, что существует Доказательство. Утверждение теоремы означает, что существует  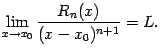 При При 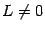 остаток остаток 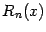 будет иметь тот же порядок малости, что будет иметь тот же порядок малости, что 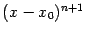 , а при , а при 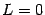 -- больший порядок малости. Итак, вычислим предел: -- больший порядок малости. Итак, вычислим предел: 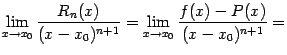 Применим к этому пределу правило Лопиталя, повторив этот приём Применим к этому пределу правило Лопиталя, повторив этот приём 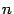 раз: раз: 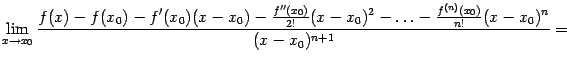 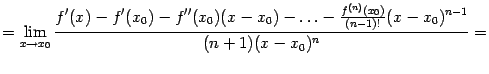 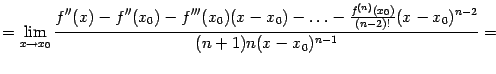 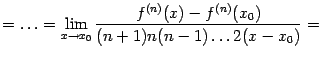 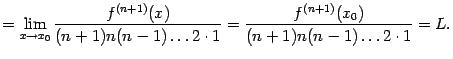 | 51. Условия монотонности функции. | 52. Экстремум функции. Необходимое условие экстремума. Пусть дана функция 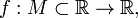 и и 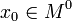 — внутренняя точка области определения f. Тогда x0 называется точкой локального максимума функции f, если существует проколотая окрестность — внутренняя точка области определения f. Тогда x0 называется точкой локального максимума функции f, если существует проколотая окрестность 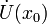 такая, что такая, что 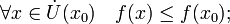 x0 называется точкой локального минимума функции f, если существует проколотая окрестность x0 называется точкой локального минимума функции f, если существует проколотая окрестность 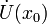 такая, что такая, что 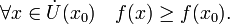 Если неравенства выше строгие, то x0 называется точкой строгого локального максимума или минимума соответственно. x0 называется точкой абсолютного (глобального) максимума, если Если неравенства выше строгие, то x0 называется точкой строгого локального максимума или минимума соответственно. x0 называется точкой абсолютного (глобального) максимума, если 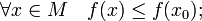 x0 называется точкой абсолютного минимума, если x0 называется точкой абсолютного минимума, если 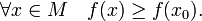 Значение функции f(x0) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума. Следующая теорема даёт необходимое условие того, чтобы точка Значение функции f(x0) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума. Следующая теорема даёт необходимое условие того, чтобы точка  была точкой локального экстремума функции была точкой локального экстремума функции  . Теорема 7.4 Если точка . Теорема 7.4 Если точка  -- это точка локального экстремума функции -- это точка локального экстремума функции  , определенной в некоторой окрестности точки х0, и существует производная в этой точке , определенной в некоторой окрестности точки х0, и существует производная в этой точке 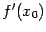 , то , то 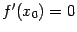 . Доказательство этой теоремы сразу же следует из теоремы Ферма (см. гл. 5). Утверждение теоремы можно переформулировать так: если функция . Доказательство этой теоремы сразу же следует из теоремы Ферма (см. гл. 5). Утверждение теоремы можно переформулировать так: если функция  имеет локальный экстремум в точке имеет локальный экстремум в точке  , то либо 1) , то либо 1) 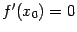 , либо 2) производная , либо 2) производная 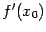 не существует. Точка не существует. Точка  называется критической точкой функции называется критической точкой функции  , если , если  непрерывна в этой точке и либо непрерывна в этой точке и либо 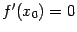 , либо , либо 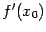 не существует. В первом случае (то есть при не существует. В первом случае (то есть при 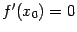 ) точка ) точка  называется также стационарной точкой функции называется также стационарной точкой функции  . Итак, локальный экстремум функции . Итак, локальный экстремум функции  может наблюдаться лишь в одной из критических точек этой функции. может наблюдаться лишь в одной из критических точек этой функции. |
54. Достаточное условие экстремума, использующее высшие производные. Пусть  -- стационарная точка функции -- стационарная точка функции  , и в этой точке существует вторая производная , и в этой точке существует вторая производная 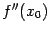 , причём , причём 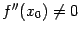 . Тогда при . Тогда при 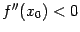 точка точка  есть точка локального максимума, а при есть точка локального максимума, а при 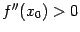 -- локального минимума. Доказательство. Поскольку -- локального минимума. Доказательство. Поскольку 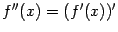 , то по определению производной , то по определению производной 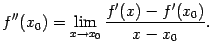 Пусть Пусть 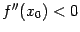 . Тогда из существования предела следует, что для любого . Тогда из существования предела следует, что для любого 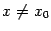 из некоторой достаточно малой проколотой окрестности из некоторой достаточно малой проколотой окрестности 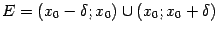 точки точки  выполняется то же неравенство для допредельного выражения, то есть выполняется то же неравенство для допредельного выражения, то есть 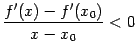 при при  . Поскольку, по предположению теоремы, . Поскольку, по предположению теоремы,  -- стационарная точка, то -- стационарная точка, то 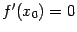 , откуда , откуда 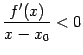 , то есть , то есть 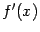 имеет знак, противоположный знаку имеет знак, противоположный знаку 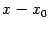 : : 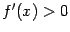 при при 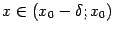 и и 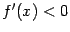 при при 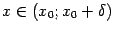 . Остаётся лишь применить теперь предыдущую теорему, из которой следует, что . Остаётся лишь применить теперь предыдущую теорему, из которой следует, что  -- точка локального максимума. Доказательство для случая -- точка локального максимума. Доказательство для случая 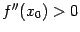 совершенно аналогично. совершенно аналогично. | 55,56. Условия выпуклости и точки перегиба графика функции. Точка перегиба функции 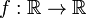 внутренняя точка x0 области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x0 является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот. Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки x0, имеет в x0 точку перегиба, то внутренняя точка x0 области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x0 является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот. Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки x0, имеет в x0 точку перегиба, то 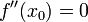 . Первое достаточное условие существования точки перегиба: если функция f(x) в некоторой окрестности точки x k раз непрерывно дифференцируема, причем k нечётно и . Первое достаточное условие существования точки перегиба: если функция f(x) в некоторой окрестности точки x k раз непрерывно дифференцируема, причем k нечётно и 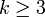 , и , и 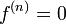 при при 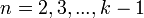 , а , а 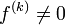 , то функция f(x) имеет в x0 точку перегиба. Второе достаточное условие существования точки перегиба: Если в некоторой точке вторая производная функции равна нулю, а третья не равна нулю, то эта точка является точкой перегиба. 56. Вертикальные и наклонные асимптоты. Асимптотой графика функции , то функция f(x) имеет в x0 точку перегиба. Второе достаточное условие существования точки перегиба: Если в некоторой точке вторая производная функции равна нулю, а третья не равна нулю, то эта точка является точкой перегиба. 56. Вертикальные и наклонные асимптоты. Асимптотой графика функции 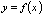 называется прямая, обладающая тем свойством, что расстояние от точки называется прямая, обладающая тем свойством, что расстояние от точки 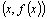 до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Прямая x = a называется вертикальной асимптотой графика функции f (x) при x → a, если выполнено хотя бы одно из условий
Прямая y = b называется горизонтальной асимптотой графика функции f (x) при x → +∞, если Прямая y = kx + b, k ≠ 0 называется наклонной асимптотой графика функции f (x) при x → +∞, если Для того, чтобы прямая y = kx + b была асимптотой графика функции y = f (x) при x → +∞, необходимо и достаточно, чтобы существовали конечные пределы Наши рекомендации
|

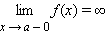 ,
, 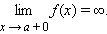
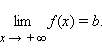
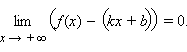 Аналогично определяются горизонтальная и наклонная асимптоты при x → –∞.
Аналогично определяются горизонтальная и наклонная асимптоты при x → –∞.