П.6.3.Как найти точку пересечения двух прямых?

Если прямые 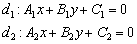пересекаются в точке 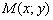, то её координаты являются решениемсистемы линейных уравнений

Как найти точку пересечения прямых? Решить систему.

Вот вам и геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще всего) прямые на плоскости.

Задачу удобно разбить на несколько этапов. Анализ условия подсказывает, что необходимо:
1) Составить уравнение одной прямой .
2) Составить уравнение второй прямой .
3) Выяснить взаимное расположение прямых .
4) Если прямые пересекаются, то найти точку пересечения.

Пример 13.

Найти точку пересечения прямых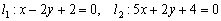

Решение: Точку пересечения целесообразно искать аналитическим методом. Решим систему:

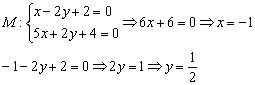
Ответ: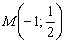

П.6.4. Расстояние от точки до прямой

Перед нами прямая полоса реки и наша задача состоит в том, чтобы дойти до неё кратчайшим путём. Препятствий нет, и самым оптимальным маршрутом будет движение по перпендикуляру. То есть, расстояние от точки до прямой – это длина перпендикулярного отрезка.

Расстояние в геометрии традиционно обозначают греческой буквой «ро», например: – расстояние от точки «эм» до прямой «дэ».

Расстояние от точки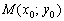 до прямой 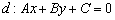выражается формулой

Пример 14.

Найти расстояние от точки 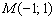до прямой

Решение: всё что нужно - аккуратно подставить числа в формулу и провести вычисления:

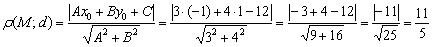
Ответ:

П.6.5. Угол между прямыми.

Пример 15.

Найти угол между прямыми .

1. Проверяем перпендикулярны ли прямые:

Вычислим скалярное произведение направляющих векторов прямых:
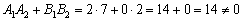, значит, прямые не перпендикулярны.
2. Угол между прямыми найдём с помощью формулы:

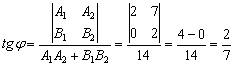
Таким образом:

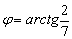
Ответ: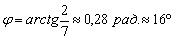

Кривые второго порядка. Окружность

Пусть на плоскости задана прямоугольная система координат 0ху.

Кривой второго порядка называется линия на плоскости, определяемая уравнением второй степени относительно текущих координат точки М(х, у, z). В общем случае это уравнение имеет вид:

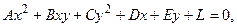
где коэффициенты А, В, С, D, E, L – любые действительные числа, причем хотя бы одно из чисел А, B, С отлично от нуля.

Далее рассмотрим четыре вида кривых второго порядка: окружность, эллипс, гипербола и парабола.

1.Окружностью называется множество точек на плоскости, расстояние от которых до фиксированной точки М₀(х₀, у₀) постоянно и равно R. Точка М₀ называется центром окружности, а число R – ее радиусом

– уравнение окружности с центром в точке М₀(х₀, у₀) и радиусом R.

Если центр окружности совпадает с началом координат, то имеем:

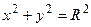
– каноническое уравнение окружности.

Эллипс.

Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух данных точек есть величина постоянная (причем эта величина больше расстояний между данными точками). Данные точки называются фокусами эллипса.

– каноническое уравнение эллипса.

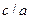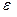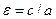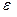Отношение называется эксцентриситетом эллипса и обозначается: , . Так как , то < 1.

Следовательно, с уменьшением 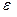отношение стремится к 1, т.е. b мало отличается от а и форма эллипса становится ближе к форме окружности. В предельном случае при , получается окружность, уравнение которой есть

х² + у² = а² .

Гипербола

Гиперболой называется множество точек на плоскости, для каждой из которых абсолютная величина разности расстояний до двух данных точек, называемыхфокусами, есть величина постоянная (при условии, что эта величина меньше расстояния между фокусами и не равна 0).

Пусть F₁, F₂ – фокусы, расстояние между ними обозначим через 2с,

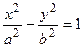
– каноническое уравнение гиперболы.

Отношение 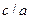называется эксцентриситетом гиперболы и обозначается , т.е. 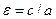. Так как , то 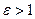. Из формулы 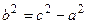имеем: ,

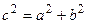Следовательно, эксцентриситет характеризует форму гиперболы.

Парабола

Параболой называется множество точек на плоскости, для каждой из которых расстояние до данной точки (называемой фокусом) равно расстоянию до данной прямой (называемой директрисой).

Пусть F – фокус, l – директриса параболы, р – расстояние от фокуса F до директрисы l (назовем р параметром параболы).

– каноническое уравнение параболы.

Заметим, что уравнение при отрицательном р также задает параболу, которая будет расположена слева от оси 0у . Уравнение описывает параболу, симметричную относительно оси 0у, лежащую выше оси 0х при р > 0 и лежащую ниже оси 0х при р < 0.