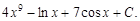Необходимые условия экстремума

Если точка M₀(x₀; y₀) является точкой локального экстремума функции f(x; y), то ее частные производные в этой точке равны нулю

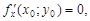
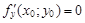
или хотя бы одна из этих производных не существует.

Точки, для которых эти условия выполнены, называются стационарными, или точками возможного экстремума.

Пример 22.Найти стационарные точки функции

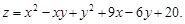
Решение

Вычислим частные производные по x и y

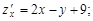
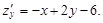
Приравняем их к нулю

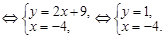
Итак, точка M₀(–4; 1) является стационарной для данной функции.

Точки экстремума всегда являются стационарными, но стационарная точка может и не быть точкой экстремума. Чтобы стационарная точка была точкой экстремума, должны выполняться достаточные условия экстремума.

Достаточные условия экстремума

Пусть в стационарной точке (x₀; y₀) и некоторой ее окрестности функция z = f(x; y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (x₀; y₀) значения

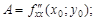
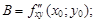
Обозначим:

Тогда:

1) если D > 0, то функция z = f(x; y) в точке (x₀; y₀) имеет экстремум:

· локальный максимум, если А < 0(или С < 0);

· локальный минимум, если А > 0(или С > 0);

2) если D < 0, то функция z = f(x; y) в точке (x₀; y₀) экстремума не имеет;

3) если D = 0, то экстремум в точке (x₀; y₀) может быть, может и не быть. Необходимы дополнительные исследования.

Исследование функции двух переменных на локальный экстремум рекомендуется проводить по следующей схеме:

1. Найти частные производные функции и

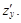
2. Решить систему уравнений 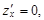и найти стационарные точки функции.

3. Найти частные производные второго порядка, вычислить их значения в каждой стационарной точке и с помощью достаточного условия сделать вывод о наличии экстремумов.

4. Найти экстремумы (экстремальные значения) функции.

Пример 23.Исследовать на экстремум функцию

Решение

1. Находим частные производные

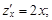
2. Находим стационарные точки функции из системы

Итак, (0; 2) – единственная стационарная точка.

3. Находим частные производные второго порядка

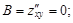
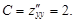
Имеем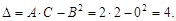

Так как D > 0, функция имеет экстремум, причем A = 2 > 0, следовательно, это локальный минимум.

4. Находим минимум функции

Тест 14.Пусть 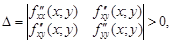то функция f(x; y) в точке M(x; y) имеет локальный максимум, если:

1)

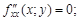
2)

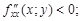
3)

4)

5)

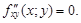
Условный экстремум

Рассмотрим задачу, специфическую для функций нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторому условию.

Пусть рассматривается функция z = f(x; y), аргументы х и у которой удовлетворяют условию j(x; y) = 0.

Экстремум функции z = f(x; y), найденный при условии j(x; y) = 0, называется условным. Уравнение j(x; y) = 0 называется уравнением связи.

Если из уравнения связи j(x; y) = 0 найти y = y(x) и подставить в функцию z = f(x; y), то задача отыскания условного экстремума сводится к нахождению экстремума функции одной переменной z = f(x; y(x)).

Пример 24. Найти экстремум функции z = x ² – y ² при условии, что 2x – y – 6 = 0.

Решение

1. Из уравнения связи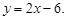

2. Подставив в данную функцию, получим функцию одной переменной x

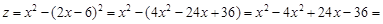
3. Находим

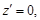т. е. –6х + 24 = 0, х = 4.

Тогда

Итак, M(4; 2) – стационарная точка.

4. Так как то в точке M(4; 2) данная функция достигает условного максимума.

5.

Наибольшее и наименьшее значения функции
в замкнутой области (глобальный экстремум)

Множество называется замкнутым, если оно включает все свои граничные точки, т. е. точки, окрестности которых содержат точки как принадлежащие множеству, так и не принадлежащие ему.

Пусть функция z = f(x; y) определена и непрерывна в ограниченной замкнутой области Тогда она достигает в некоторых точках своего наибольшего и наименьшего значений. Эти значения достигаются функцией в точках, расположенных внутри области или в точках, лежащих на границе области.

Для нахождения наибольшего и наименьшего значений функции в необходимо:

1. Найти стационарные точки функции, принадлежащие 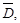и вычислить значения функции в них.

2. Найти наибольшее и наименьшее значения функции z = f(x; y) на границах области.

Добавим, что, как правило, граница состоит из совокупности отдельных участков, на каждом из которых задача сводится к исследованию на экстремум функции одной переменной 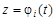, где i – номер участка, а t – независимая переменная на этом участке, которая может совпасть с x или y либо быть отдельным параметром.

3. Сравнить все найденные значения функции и выбрать из них наибольшее и наименьшее.

Пример 25.Найти глобальный экстремум функции 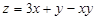в замкнутой области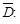

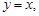
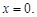
Решение

1. Построим (рисунок 44).

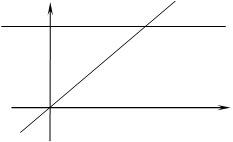
Рисунок 44

2. Находим стационарные точки из следующей системы:

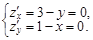
Откуда х = 1, у = 3. Получим одну стационарную точку М₁(1; 3), которая лежит в области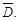

Итак,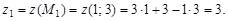

3. Исследуем данную функцию на границе области 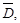состоящей из участков ОВ, ВА, АО. Кроме того, необходимо учесть и концы отрезков, т. е. точки О, В, А:

· Составим уравнения для ОВ: х = 0.

Подставим его в z:

Получили функцию одной переменной, которую исследуем на экстремум.

Находим 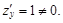Следовательно, на ОВ нет стационарных точек.

На концах отрезка ОВ

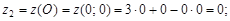
· Аналогично все точки прямой ВА удовлетворяют уравнению у = 4.

Тогда На ВА нет стационарных точек.

В точке А:

· Уравнение прямой АО имеет вид у = х.

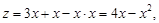
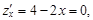
Тог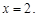да Тогда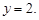

Итак, М₂(2; 2) – стационарная точка.

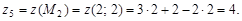
На концах отрезка АО значения функции уже найдены.

4. Сравнивая все полученные значения функции z, заключаем, что 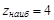достигается в точках B(0; 4) и М₂(2; 2), а – в точках O(0; 0) и A(4; 4).

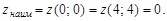
Эмпирические формулы

При анализе экономических процессов часто приходится решать задачу приближенного представления (аппроксимации) заданных функций другими, более простыми.

Пусть зависимость между двумя переменными x и y выражается в виде таблицы 1, полученной опытным путем. Это могут быть результаты опыта или наблюдений, статистических данных за ряд лет и т. п.

Таблица 1

x	x1	x2	…	xi	…	xn
y	y1	y2	…	yi	…	yn

Требуется наилучшим образом сгладить экспериментальную зависимость между переменными x и y, т. е. по возможности точно отразить общую тенденцию зависимости y от x, исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений. Такую сглаженную зависи-
мость стремятся представить в виде формулы y = f(x).

Формула y = f(x), полученная на основании экспериментальных данных, называется эмпирической.

Выбор эмпирической функции зависит от теоретических исследований и характера расположения на плоскости Oxy экспериментальных точек

Обычно для экономических исследований достаточно одной из шести следующих формул:

1) – линейная;

2) 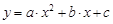– параболическая;

3) 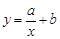– гиперболическая;

4) 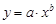– показательная;

5) 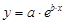– экспоненциальная.

Выбранная для приближения формула называется теоретической.

После выбора вида формулы требуется найти значения определяющих ее параметров таким образом, чтобы отклонения значений функции от экспериментальных значений были минимальными (a, b, c).

Суть метода наименьших квадратов изложим на примере линейной зависимости 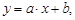где параметры подлежат определению из системы нормальных уравнений

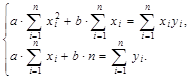(5)

В случае квадратичной зависимости параметры определяют из нормальной системы

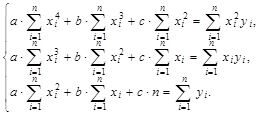(6)

Пример 26.Результаты измерений величин x и y приведены в таблице 2.

Таблица 2

x	–2	–1
y	5,6		4,3		3,6

Решение

Требуется установить зависимость между этими величинами и определить параметры эмпирической формулы. Если принять пары значений (x_i; y_i) за координаты точек в декартовой системе координат, то на чертеже (рисунок 45) видно, что точки располагаются приблизительно на одной прямой, уравнение которой может быть записано в виде y = ax + b.

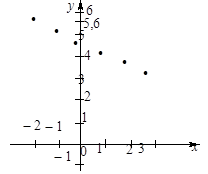
Рисунок 45

Определив a и b с помощью системы (5), найдем линейную зависимость y = ax + b между величинами x и y.

Подсчитаем необходимые суммы, используя таблицу 3.

Таблица 3

i	x	y	x × y	x2
	–2	5,6	–11,2
	–1		–5
		4,3
		3,6	7,2
S		25,5

В последней строке таблицы записаны коэффициенты системы уравнений (5), которая принимает вид

Решая эту систему, находим а = –0,5, b = 4,5. Требуемая зависимость имеет вид

Тест 15.Установить вид функции y = f(x) (рисунок 46)

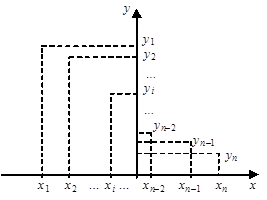
Рисунок 46

по характеру расположения на координатной плоскости экспериментальных точек:

1)

2)

3)

4)

5)

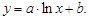
Тест 16.Метод наименьших квадратов позволяет находить:

1) вид функции двух переменных;

2) градиент функции двух переменных;

3) экстремум функции;

4) параметры эмпирических формул;

5) частные производные функции нескольких переменных.

Ответы на тестовые задания

Номер теста
Правильный ответ

Номер теста
Правильный ответ

2.8. Первообразная и неопределенный интеграл

Множество вопросов математического анализа и приложений в разнообразных науках приводят к задаче отыскания для данной функции f(x) такой функции F(x), производная которой равна f(x).

Определение. Дифференцируемая функция F(x) называется первообразной по отношению к функции f(x) на некотором интервале
(а; b), если при F¢(x) = f(x).

Определение. Общее выражение F(x) + C множества всех первообразных функций для данной функции f(x) называется неопределенным интегралом от f(x) и обозначается 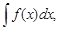т. е. 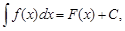где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, – знак неопределенного интеграла, х – переменная интегрирования.

Операция нахождения первообразной по ее производной или неопределенного интеграла по заданной подынтегральной функции называется интегрированием этой функции. Интегрирование является операцией, обратной дифференцированию.

Основные свойства неопределенного интеграла следующие:

1. Производная от неопределенного интеграла равна подынтегральной функции, т. е.

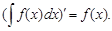
2. Постоянный множитель можно вынести за знак неопределенного интеграла, т. е.

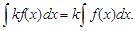
3. Неопределенный интеграл от алгебраической суммы нескольких функций равен соответствующей алгебраической сумме от функций-слагаемых, т. е.

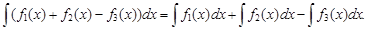
Таблица неопределенных интегралов включает следующие формулы:

1) (

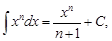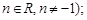
2) |x| + C;

3)

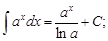
4)

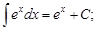
5)

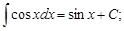
6)

7)

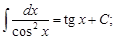
8)

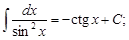
9)

10)

Приведенные выше интегралы принято называть табличными.

Как известно, операция дифференцирования не выводит функцию из класса элементарных. С операцией интегрирования обстоит иначе: первообразные от некоторых элементарных функций уже не являются элементарными функциями. Укажем некоторые из них:

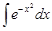· – интеграл Пуассона (интеграл ошибок);

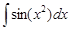· – интеграл Френеля;

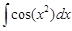· – интеграл Френеля;

· – интегральный логарифм;

· – интегральный синус;

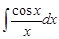· – интегральный косинус.

Пример 1. Найти неопределенный интеграл

Решение

По формуле 1 таблицы неопределенных интегралов имеем

Тест 1. Найти неопределенный интеграл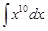

1)

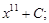
2)

3)

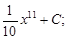
4)

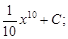
5)

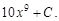
Пример 2.Найти неопределенный интеграл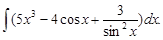

Решение

По свойствам 2 и 3 неопределенного интеграла и таблице неопределенных интегралов имеем

+
+

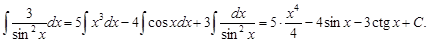
Тест 2. Найти неопределенный интеграл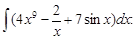

1)

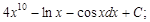
2)

3)

4)

5)