Производная и дифференциал сложной функции нескольких переменных

Пусть z=ƒ(х;у) — функция двух переменных х и у, каждая из которых является функцией независимой переменной t: х = x(t), у = y(t). В этом случае функция z = f(x(t);y(t)) является сложной функцией одной независимой переменной t; переменные х и у — промежуточные переменные.

Теорема 44.4. Если z = ƒ(х;у) — дифференцируемая в точке М(х;у) є D функция и х = x(t) и у = y(t) — дифференцируемые функции независимой переменной t, то производная сложной функции z(t) = f(x(t);y(t)) вычисляется по формуле

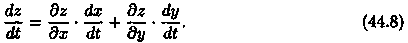
Дадим независимой переменной t приращение Δt. Тогда функции х = = x(t) и у = y{t) получат приращения Δх и Δу соответственно. Они, в свою очередь, вызовут приращение Az функции z.

Так как по условию функция z — ƒ(х;у) дифференцируема в точке М(х; у), то ее полное приращение можно представить в виде

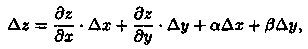
где а→0, β→0 при Δх→0, Δу→0 (см. п. 44.3). Разделим выражение Δz на Δt и перейдем к пределу при Δt→0. Тогда Δх→0 и Δу→0 в силу непрерывности функций х = x(t) и у = y(t) (по условию теоремы — они дифференцируемые). Получаем:

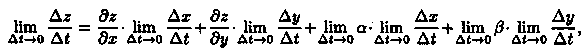
т. е.

или

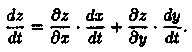
Частный случай: z=ƒ(х;у), где у=у(х), т. е. z=ƒ(х;у(х)) — сложная функция одной независимой переменной х. Этот случай сводится к предыдущему, причем роль переменной t играет х. Согласно формуле (44.8) имеем:

Формула (44.9) носит название формулы полной производной.

Общий случай: z=ƒ(х;у), где x=x(u;v), у=у(u;v). Тогда z= f(x(u;v);y(u;v)) — сложная функция независимых переменных u и v. Ее частные производные 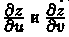можно найти, используя формулу (44.8) следующим образом. Зафиксировав v, заменяем в ней 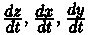соответствующими частными производными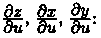

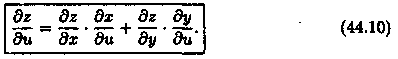
Аналогично получаем: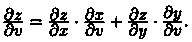

Таким образом, производная сложной функции (z) по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции (z) по ее промежуточным переменным (х и у) на их производные по соответствующей независимой переменной (u и v).

Пример 44.5. Найти 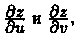если z=ln(x²+у²), х=u•v, у=u/v.

Решение: Найдем dz/du (dz/dv — самостоятельно), используя формулу (44.10):

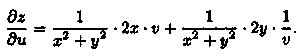
Упростим правую часть полученного равенства:

т. е.

40. Частные производные и полный дифференциал функции нескольких переменных.

Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆_хz. Итак,

Δ_хz=ƒ(х+Δх;у)-ƒ(х;у).

Аналогично получаем частное приращение z по у:

Δ_уz=ƒ(x;у+Δу)-ƒ(х;у).

Полное приращение Δz функции z определяется равенством

Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у).

Если существует предел

то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов:

Частные производные по х в точке М₀(х₀;у₀) обычно обозначают символами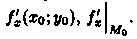

Аналогичноопределяется и обозначается частная производная от z=ƒ(х;у) по переменной у:

Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ(х;у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).

Пример 44.1. Найти частные производные функции z = 2у + е^{х2-у +1}. Решение:

Геометрический смысл частных производных функции двух переменных

Графиком функции z= ƒ (х; у) является некоторая поверхность (см. п. 12.1). График функции z = ƒ (х; у₀) есть линия пересечения этой поверхности с плоскостью у = у_о. Исходя из геометрического смысла производной для функции одной переменной (см. п. 20.2), заключаем, что ƒ'x(х_о;у_о) = tg а, где а — угол между осью Ох и касательной, проведенной к кривой z = ƒ (х; у₀) в точке Мо(хо;уо; ƒ(хо;уо)) (см. рис. 208).

Аналогично, f'y (х₀;у₀)=tgβ.

Функция Z=f(x,y) называется дифференцируемой в точке P(x,y), если ее полное приращение ΔZ можно представить в виде Δz = A∙Δx+B∙Δy+ω(Δx,Δy), где Δx и Δy – любые приращения соответствующих аргументов x и y в некоторой окрестности точки Р, А и В – постоянные (не зависят от Δx,Δy),

ω(Δx,Δy) – бесконечно малое более высокого порядка, чем расстояние:

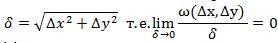
Если функция дифференцируема в точке, то ее полное приращение в этой точке состоит из двух частей :

1. Главной части приращения функции A∙Δx+B∙Δy – линейное относительно Δx,Δy

2. И нелинейное ω(Δx,Δy) – бесконечно малое более высокого порядка, чем главная часть приращения.

Главная часть приращения функции – линейная относительно Δx,Δy называется полным дифференциалом этой функции и обозначается: Δz = A∙Δx+B∙Δy, Δx=dx и Δy=dy или полный дифференциал функции двух переменных:

Дифференциал отображения. Дифференциал и производная числовой функции одной переменной. Таблица производных. Дифференцируемость.

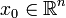Дифференциалом отображения в точке называют линейный оператор 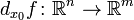такой, что выполняется условие

Отображение называется дифференцируемым в точке 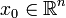если определён дифференциал .

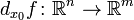Определение.Функция y=f(x) называется дифференцируемой в точке х, если ее приращение Δу в этой точке можно представить в виде

,

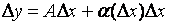где А – некоторое число, не зависящее от , а α( ) – функция аргумента , являющаяся бесконечно малой при →0, т.е.

Выясним теперь связь между дифференцируемостью в точке и существованием производной в той же точке.

Теорема. Для того чтобы функция f(x) была дифференцируемой в данной точке х , необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Таблица производных.