Теоремы Коши (1789-1857 фр.).
Кусочно-гладкую кривую, не имеющую точек самопересечения, будем называть замкнутым контуром и обозначать С. За положительный обход примем такой обход контура, когда область остается слева от направления движения. Можно получить условия независимости от формы пути интегрирования интеграла от функции комплексной переменой. Оказывается, что если функция f(z)непрерывна и области D,то необходимым и достаточным условием независимости интеграла 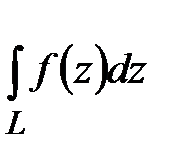 от формы пути L является аналитичность функции f(z) в области D. Сначала докажем достаточность (теоремы Коши), а в дальнейшем необходимость (теорема Морера).
от формы пути L является аналитичность функции f(z) в области D. Сначала докажем достаточность (теоремы Коши), а в дальнейшем необходимость (теорема Морера).
Теорема 2.(теорема Коши для односвязной области). Пусть функция f(z) аналитическая в односвязной области D, тогда интеграл по любому замкнутому контуру, целиком лежащему в D, будет равен нулю, т.е.  .
.
□ По условию теоремы 1 интеграл существует, т.к. функция f(z) аналитическая и ее действительная и мнимая части непрерывны и дифференцируемы в области D, а сам интеграл можно записать: 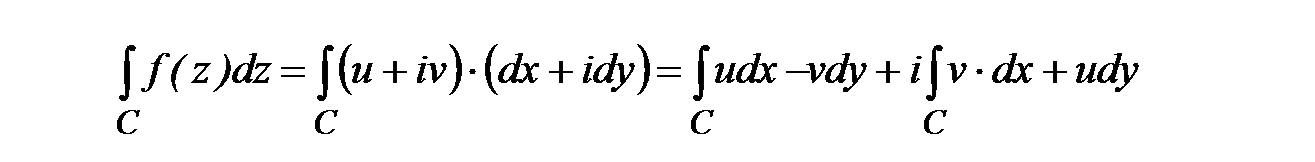 . (3)
. (3)
Воспользуемся формулой Грина: 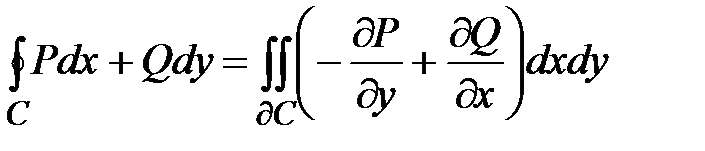 , тогда учитывая условия Коши-Римана
, тогда учитывая условия Коши-Римана 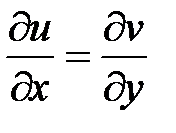 ,
, 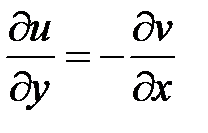 , получим
, получим
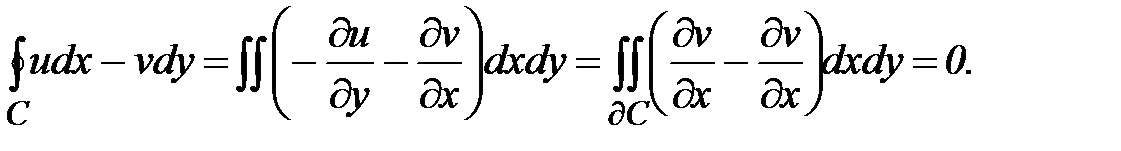
Аналогично получим, что 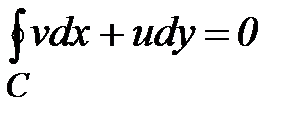 и из (3) следует, что интеграл от аналитической функции комплексной переменной равен нулю. ■
и из (3) следует, что интеграл от аналитической функции комплексной переменной равен нулю. ■
Теорема 3.(вторая формулировка теоремы Коши). Пусть функция f(z) аналитическая в односвязной области D, границы которой является контур C и непрерывна в замыкании: 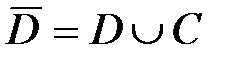 ,тогда
,тогда 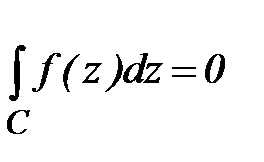 .
.
Теорема 4.(теорема Коши для многосвязной области) Пусть функция f(z) аналитическая в многосвязной области D, ограниченной внешним контуром С и внутренними контурами С1,С2,…Сnи непрерывна в замкнутой области 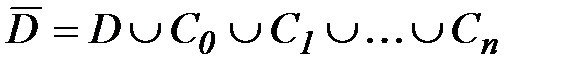 ,тогда интеграл по внешней границе
,тогда интеграл по внешней границе  , проходимой в положительном направлении равен сумме интегралов по внутренним границам С1,С2,…Сn
, проходимой в положительном направлении равен сумме интегралов по внутренним границам С1,С2,…Сn
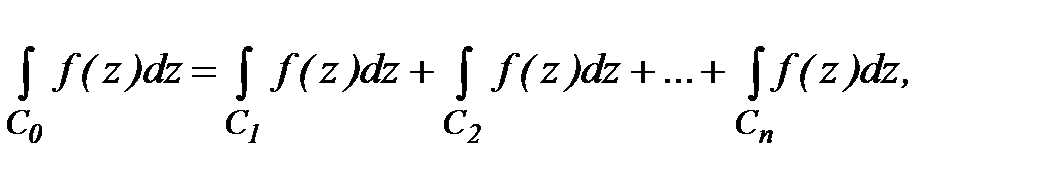
причем все интегралы проходятся против часовой стрелки.
□ Соединим внутренние контуры Ск с внешним контуром С0 кусочно-гладкими кривыми 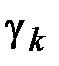 . Пусть кривые
. Пусть кривые 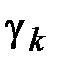 обходятся дважды: от контура С0, потом к нему. В этом случае интеграл по общей границе области
обходятся дважды: от контура С0, потом к нему. В этом случае интеграл по общей границе области 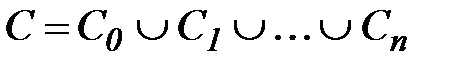 по теореме Коши будет равен нулю, т.к. область D можно рассматривать как односвязную с разрезами по кривым
по теореме Коши будет равен нулю, т.к. область D можно рассматривать как односвязную с разрезами по кривым 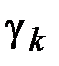 .
.
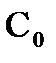
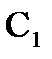
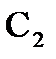
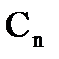
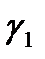
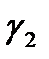
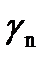
Рис.4.
Тогда
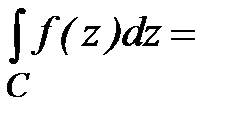
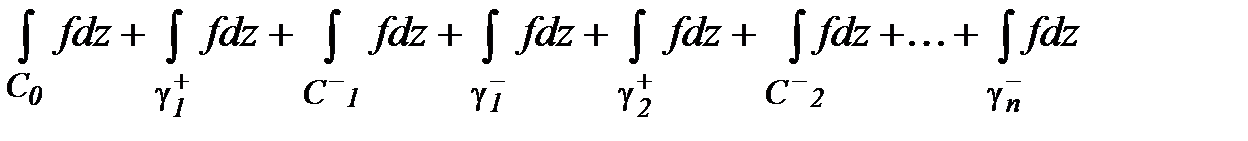 По свойству ориентированности интегралы по
По свойству ориентированности интегралы по 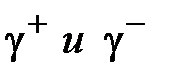 равны по абсолютной величине и противоположны по знаку, следовательно, их сумма равна нулю , а у интегралов по внутренним контурам изменим ориентацию
равны по абсолютной величине и противоположны по знаку, следовательно, их сумма равна нулю , а у интегралов по внутренним контурам изменим ориентацию
и в итоге получаем: 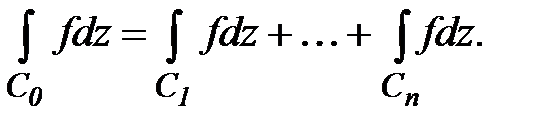
Следствие.Если функция f(z) аналитическая в двусвязной области D, ограниченной контурами С1 и С2, то 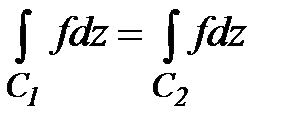 . Другими словами, контуры интегрирования можно как угодно деформировать не выходя за пределы области аналитичности функции.
. Другими словами, контуры интегрирования можно как угодно деформировать не выходя за пределы области аналитичности функции.
С С1
С
Рис.5.
Замечание 1. Если область не односвязная, то интеграл не по любому контуру равен нулю.
Пример 4.Задана область D- кольцо: 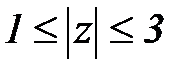 и функция
и функция 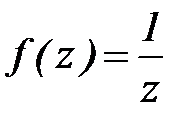 . Найти интеграл по окружности
. Найти интеграл по окружности 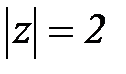 .
.
Решение. 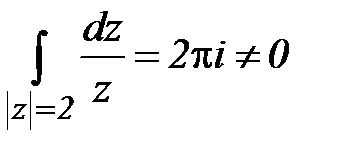 , при этом функция в области
, при этом функция в области 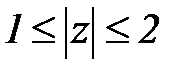 является аналитической.
является аналитической.
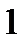
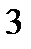
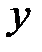
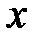
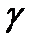
Рис.6.
По кривой 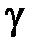 интеграл будет равен нулю, а по обхватывающей окружности
интеграл будет равен нулю, а по обхватывающей окружности 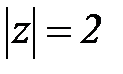 не будет равен нулю.
не будет равен нулю.
| y |
z
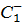 |
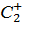 |
| x |
| O |
На рисунке 7 контур 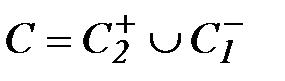 будет замкнутым. По теореме Коши
будет замкнутым. По теореме Коши
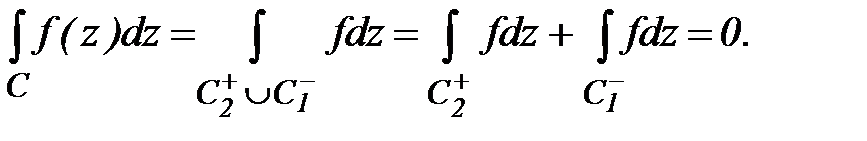
Отсюда имеем 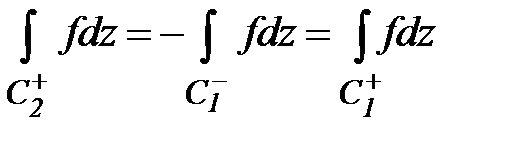 .
.
Получили, что интеграл не зависит от кривой интегрирования, а зависит только от положения начальной и конечной точек. Поэтому, если z0 фиксированная точка, z переменная точка, то можно записать 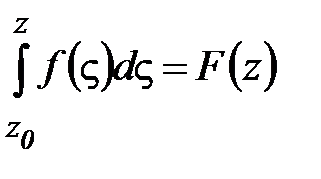 , где F(z)- функция переменного верхнего предела.
, где F(z)- функция переменного верхнего предела.
Теорема 5.Если функция f(z) определена и непрерывна в односвязной области D и интеграл по любому замкнутому контуру, целиком лежащем в D равен нулю, то функция 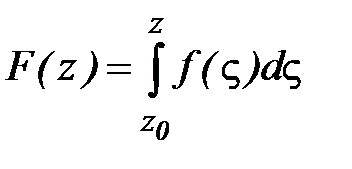 является аналитической в D, причем
является аналитической в D, причем 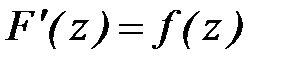 .
.
□ Запишем разностное отношение: 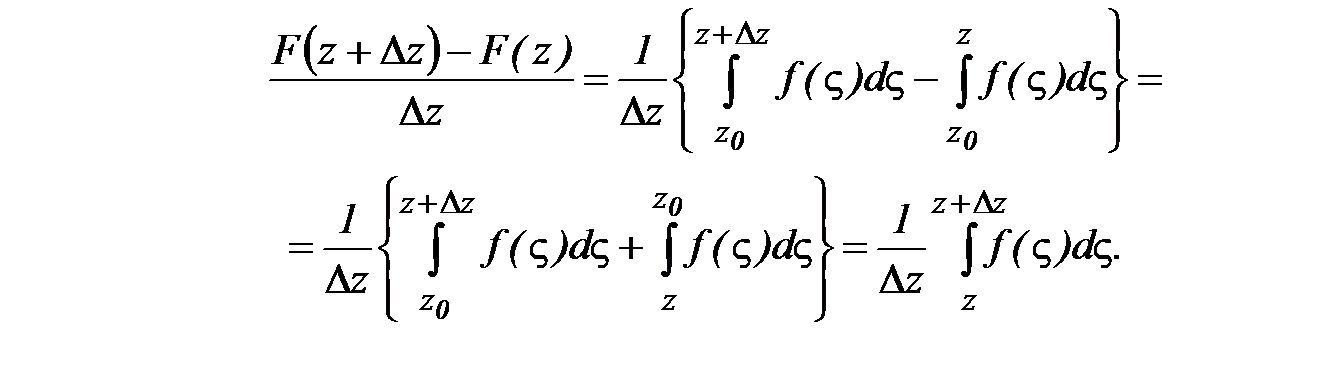
Найдем оценку следующего выражения: 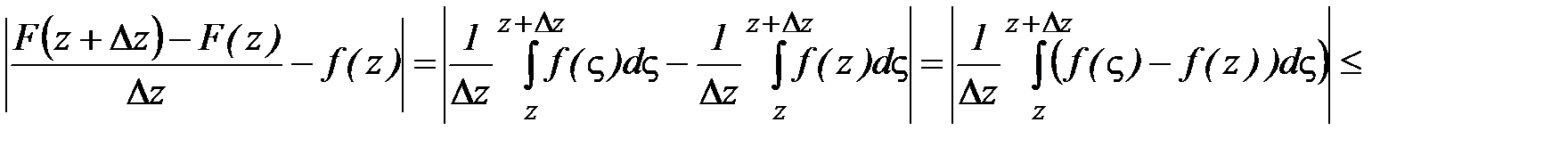
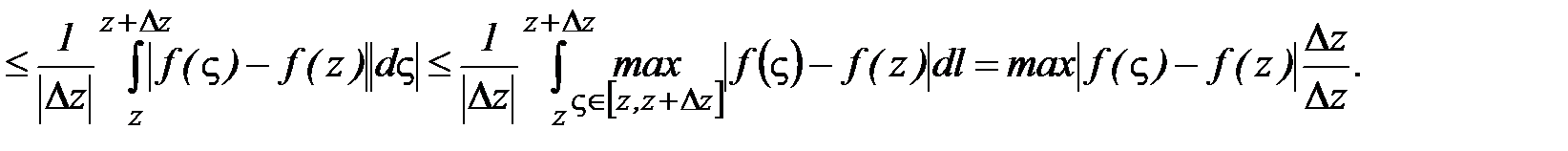
 Т.к. f(z)непрерывна в области D, то
Т.к. f(z)непрерывна в области D, то 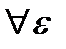 >0
>0 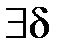 >0, если при
>0, если при 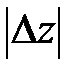 <
< 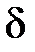 :
: 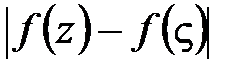 <ε.Это будет выполняться
<ε.Это будет выполняться 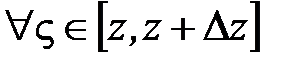 . В результате получаем, что
. В результате получаем, что 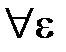 >0
>0 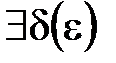 >0, если
>0, если 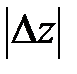 <
< 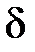 , то
, то 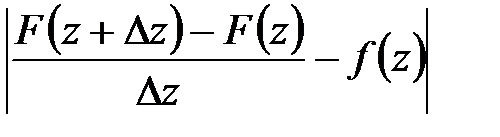 <ε
<ε
Последнее неравенство означает, что 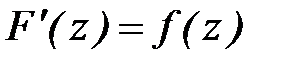 . ■
. ■
Определение 2. Аналитическая функция 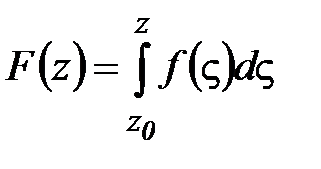 называется первообразной функции
называется первообразной функции 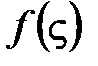 в области D, если
в области D, если 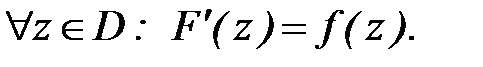
Множество всех первообразных функций f(z) называется неопределенным интегралом. Для интеграла от аналитической функции справедлива формула Ньютона-Лейбница: 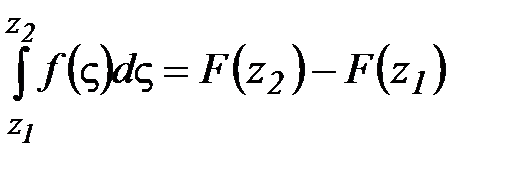 .
.
