Квадратная матрица и смежные определения

Матрица как запись коэффициентов системы линейных уравнений

Систему из m уравнений с n неизвестными

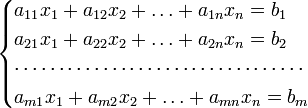
можно представить в матричном виде

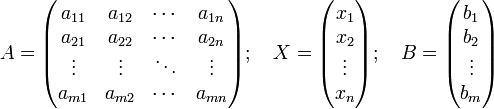
и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_ij системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{- 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{- 1}AX = A ^{- 1}B

A ^{− 1}A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{- 1}B.

Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.

Операции над матрицами

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

c_ij = a_ij + b_ij

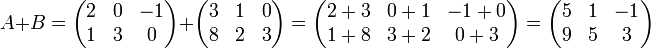
Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

c_ij = a_ij - b_ij

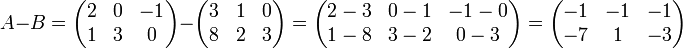
Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

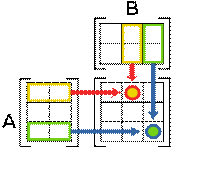
Умножение матриц (обозначение: AB, реже со знаком умножения 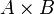) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

cij =	∑	aikbkj
	k

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность 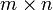, B — 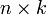, то размерность их произведения AB = C есть 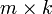. Умножение матриц не коммутативно.

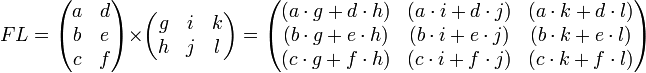
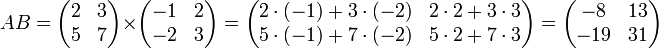
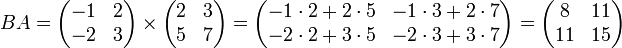
Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

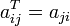
Если A — матрица размера 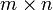, то A^T — матрица размера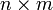

Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

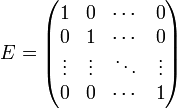
Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A ^{- 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

AA ^{− 1} = E

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности 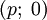на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

Свойства матриц

1. A + (B + C) = (A + B) + C

2. A + B = B + A

3. A(BC) = (AB)C

4. A(B + C) = AB + AC

5. (B + C)A = BA + CA

6.

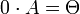
7.

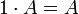
8.

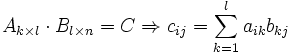
9. (A^T)^T = A

10. (A * B)^T = B^T * A^T

Вообще говоря, умножение матриц не коммутативно:

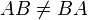
Используя это свойство, вводят коммутатор матриц.