Приведение квадратичных форм к каноническому

виду.

Рассмотрим некоторое линейное преобразование А с матрицей .

Это симметрическое преобразование можно записать в виде:

y₁ = a₁₁x₁ + a₁₂x₂

y₂ = a₁₂x₁ + a₂₂x₂

где у₁ и у₂ – координаты вектора 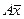в базисе .

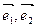Очевидно, что квадратичная форма может быть записана в виде

Ф(х₁, х₂) = х₁у₁ + х₂у₂.

Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х₁ и х₂ – скалярное произведение .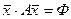

Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

.

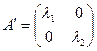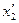При переходе к новому базису от переменных х₁ и х₂ мы переходим к переменным и . Тогда:

Тогда .

Выражение называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

Пример. Привести к каноническому виду квадратичную форму

Ф(х₁, х₂) = 27 .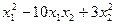

Коэффициенты: а₁₁ = 27, а₁₂ = 5, а₂₂ = 3.

Составим характеристическое уравнение: ;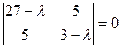

(27 - l)(3 - l) – 25 = 0

l² - 30l + 56 = 0

l₁ = 2; l₂ = 28;

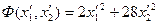
Пример. Привести к каноническому виду уравнение второго порядка:

17x² + 12xy + 8y² – 20 = 0.

Коэффициенты а₁₁ = 17, а₁₂ = 6, а₂₂ = 8. А =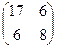

Составим характеристическое уравнение: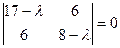

(17 - l)(8 - l) - 36 = 0

136 - 8l - 17l + l² – 36 = 0

l² - 25l + 100 = 0

l₁ = 5, l₂ = 20.

Итого: - каноническое уравнение эллипса.

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение: Составим характеристическое уравнение квадратичной формы : при

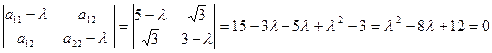
Решив это уравнение, получим l₁ = 2, l₂ = 6.

Найдем координаты собственных векторов:

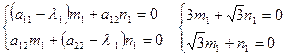полагая m₁ = 1, получим n₁ =

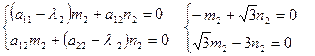полагая m₂ = 1, получим n₂ =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение: Составим характеристическое уравнение квадратичной формы : при

Решив это уравнение, получим l₁ = 1, l₂ = 11.

Найдем координаты собственных векторов:

полагая m₁ = 1, получим n₁ =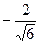

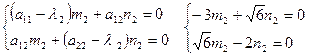полагая m₂ = 1, получим n₂ =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

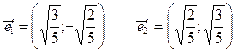
Имеем следующее уравнение линии в новой системе координат:

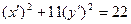
Каноническое уравнение линии в новой системе координат будет иметь вид:

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

4ху + 3у² + 16 = 0

Коэффициенты: a₁₁ = 0; a₁₂ = 2; a₂₂ = 3.

Характеристическое уравнение:

Корни: l₁ = -1, l₂ = 4.

Для l₁ = -1 Для l₂ = 4

m₁ = 1; n₁ = -0,5; m₂ = 1; n₂ = 2;

= (1; -0,5) = (1; 2)

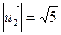
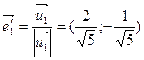
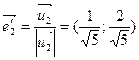
Получаем: -каноническое уравнение гиперболы.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая решает рассморенные выше примеры для любых начальных условий.

Для запуска программы дважды щелкните на значке:

В открывшемся окне программы введите коэффициенты квадратичной формы и нажмите Enter.

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Введение в математический анализ.

Числовая последовательность.