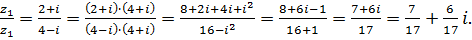Тема «неопределённый интеграл. метод интегрирования по частям.
Министерство образования Тверской области
ГБПОУ «Тверской колледж им. А.Н. Коняева»
Математика
Методические рекомендации
для выполнения домашней работы по дисциплине «Математика»
(для студентов-заочников)
Тверь 2016 г
Одобрено предметной (цикловой) Заместитель директора
комиссией по учебной работе
Председатель: Лабудина И.А. Лукина Н.С.
____________________ _____________________
Составил: Бодров Е.Н.
__________________
Учебное пособие содержит материал по темам «Пределы», «Производная», «Интеграл», «Комплексные числа». Пособие предназначено для студентов-заочников, изучающих дисциплину «Математика»
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ. 4
ЗАДАНИЯ ДОМАШНЕЙ РАБОТЫ И РЕКОМЕНДАЦИИ ПО ИХ ВЫПОЛНЕНИЮ 5
СПИСОК ЛИТЕРАТУРЫ.. 12
ПРИЛОЖЕНИЯ.. 13
ВВЕДЕНИЕ
Перед выполнением домашней работы студентам рекомендуется изучить соответствующие темы по учебникам указанным в списке литературы.
При выполнении домашней работы следует руководствоваться следующими требованиями.
1. Работа должна быть представлена в срок, установленный графиком учебного процесса.
2. Работа должна быть правильно оформлена и выполнена четким, разборчивым почерком без применения сокращений слов. Страницы должны быть пронумерованы и иметь поля для замечаний преподавателя.
3. В начале работы должен быть указан номер варианта. Номер варианта работы соответствует последней цифре зачётной книжки студента.
4. Последовательность изложения решений задач должна соответствовать их номерам в домашней работе.
5. Перед решением задач необходимо указать их номер и полностью привести условие.
6. Решение задания должно завершаться ответом с указанием искомых величин и их значений.
7. Решение задач следует представлять в развернутом виде с краткими пояснениями и подробными арифметическими расчетами. При этом сначала необходимо привести определение и выражение для вычисления искомой характеристики. Задачи, в которых приводятся только ответы без промежуточных вычислений, считаются нерешенными.
8. Титульный лист работы должен быть корректно оформлен.
Студенты, не выполнившие домашнюю работу или не устранившие замечания преподавателя, к сдаче зачёта не допускаются.
ЗАДАНИЯ ДОМАШНЕЙ РАБОТЫ И РЕКОМЕНДАЦИИ ПО ИХ ВЫПОЛНЕНИЮ
Тема «Пределы»
Задание №1.Вычислить пределы.
1. а) 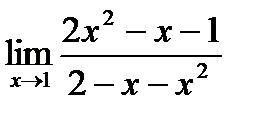 ; б) ; б) 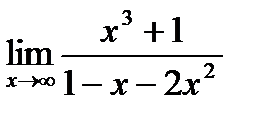 в) в) 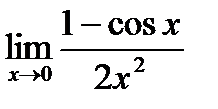 . 2. а) . 2. а) 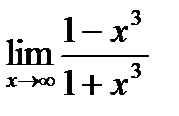 ;б) ;б) 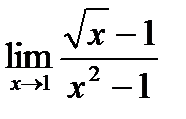 ;в) ;в) 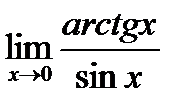 . 3. а) . 3. а) 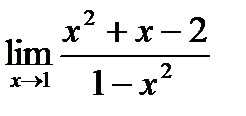 ;б) ;б) 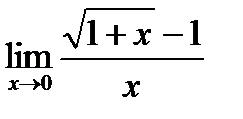 ;) ;) 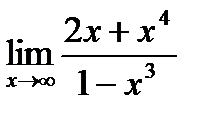 . 4. а) . 4. а) 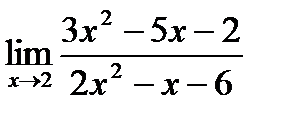 ;б) ;б) 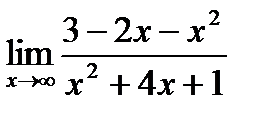 ; в) ; в) 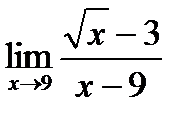 . 5. а) . 5. а) 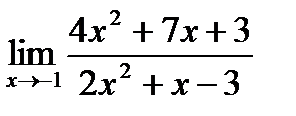 ;б) ;б) 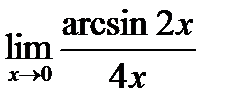 ;в) ;в) 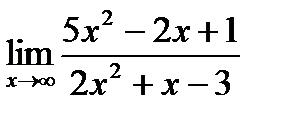 . 6. а) . 6. а) 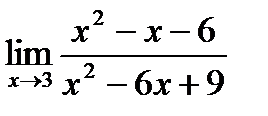 ;б) ;б) 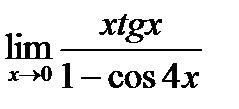 ;в) ;в) 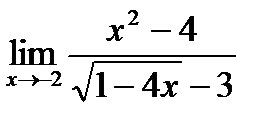 . 7.а) . 7.а) 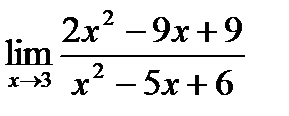 ;б) ;б) 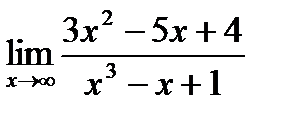 ; в) ; в) 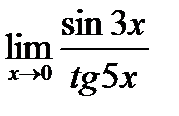 . 8. а) . 8. а) 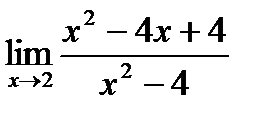 ;б) ;б) 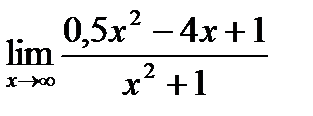 ;в) ;в) 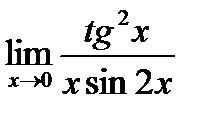 . 9. а) . 9. а) 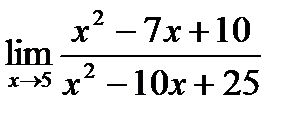 ; б) ; б) 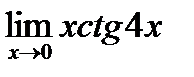 ; в) ; в) 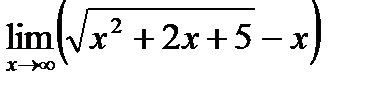 . 10. а) . 10. а) 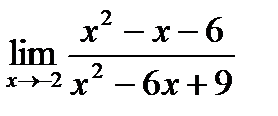 ; б) ; б) 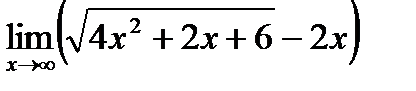 ; в) ; в) 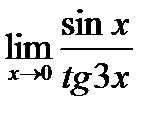 . . |
Решение типового примера. Найти пределы
а) 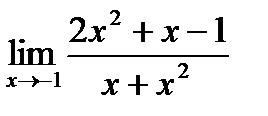 . При
. При 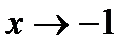 и числитель и знаменатель дроби, стремятся к нулю (неопределенность
и числитель и знаменатель дроби, стремятся к нулю (неопределенность 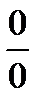 ). Для
). Для
раскрытия неопределенности разложим многочлен и в числителе и знаменателе на линейные множители и сократим дробь. Получим,
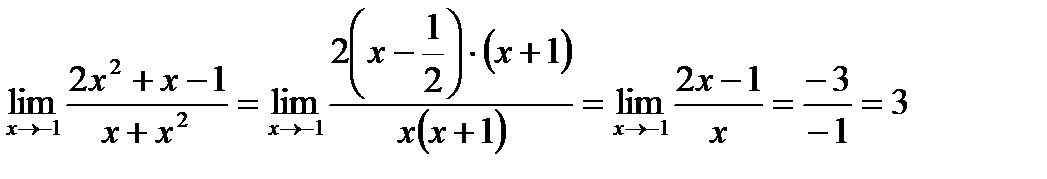 .
.
б) 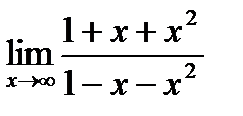 . При
. При 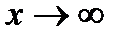 числитель и знаменатель дроби стремятся к
числитель и знаменатель дроби стремятся к 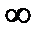 (неопределенность
(неопределенность 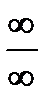 ). Для раскрытия неопределенности разделим числитель и знаменатель на х2 (х2 – самая высокая степень х). Получим,
). Для раскрытия неопределенности разделим числитель и знаменатель на х2 (х2 – самая высокая степень х). Получим,
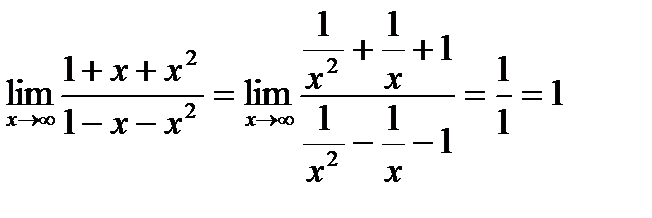 .
.
в) 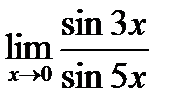 . Для раскрытия неопределенности
. Для раскрытия неопределенности 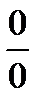 воспользуемся правом замены эквивалентных бесконечно малых сомножителей (приложения, таблица 5). В нашем случае
воспользуемся правом замены эквивалентных бесконечно малых сомножителей (приложения, таблица 5). В нашем случае 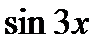 ~3х, sin5x~5х. Поэтому,
~3х, sin5x~5х. Поэтому, 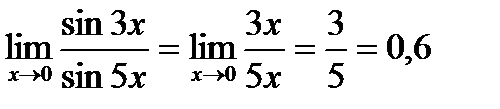 .
.
г) 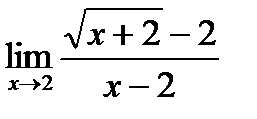 . Для раскрытия неопределенности
. Для раскрытия неопределенности 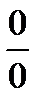 числитель и знаменатель умножим на сопряженную величину
числитель и знаменатель умножим на сопряженную величину 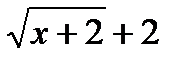 . Получим,
. Получим,
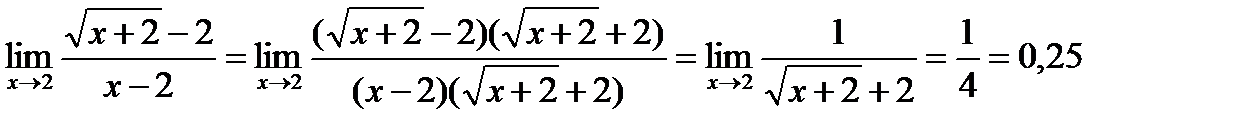 .
.
ТЕМА «ПРОИЗВОДНАЯ ФУНКЦИИ»
Задание №2.Найти производные функций, пользуясь правилами и формулами дифференцирования.
| 1. | а) 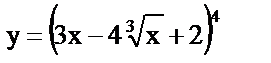 , , |
б) 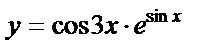 , , | |
| 2. | а) 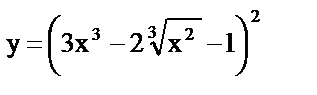 , , |
б) 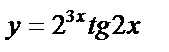 , , | |
| 3. | а) 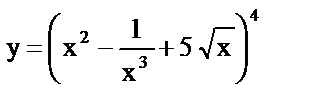 , , |
б) 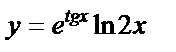 , , | |
| 4. | а) 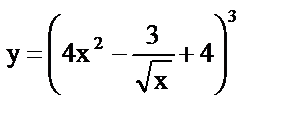 , , |
б) 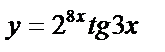 , , | |
| 5. | а) 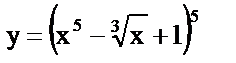 , , |
б) 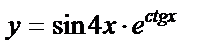 , , | |
| 6. | а) 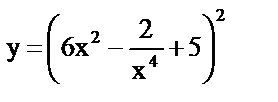 , , |
б) 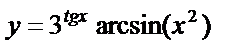 , , | |
| 7. | а) 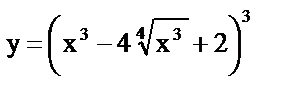 , , |
б) 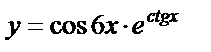 , , | |
| 8. | а) 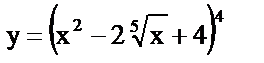 , , |
б) 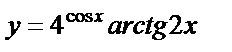 , , |
| 9. | а) 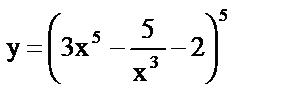 , , |
б) 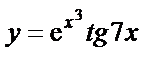 , , | |
| 10. | а) 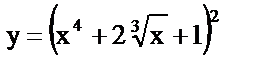 , , |
б) 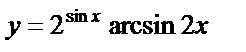 , , |
Решение типового примера
Для нахождения производных надо использовать таблицу производных от основных элементарных функций (приложения, таблица 1),
а также пользоваться арифметическими свойствами производной (приложения, таблица 2) и правилом дифференцирования сложной функции 

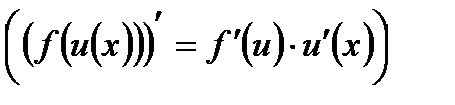 .
.
Например, найти производную функции 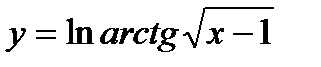 . Данная функция является сложной и имеет вид:
. Данная функция является сложной и имеет вид: 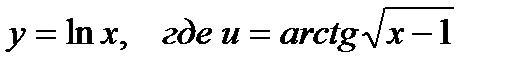 . Поэтому,
. Поэтому, 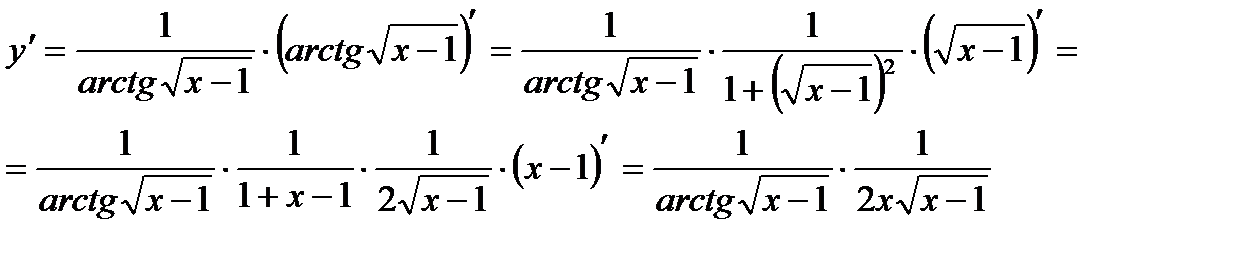
При вычислении производной мы пользовались формулами:
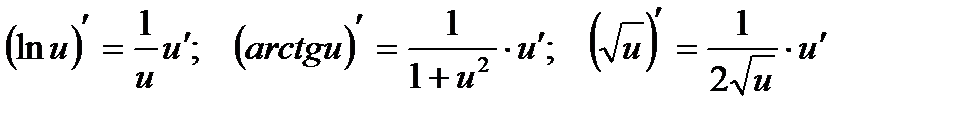 .
.
ТЕМА «НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. МЕТОД ПОДСТАНОВКИ»
Задание №3. Найти неопределенные интегралы методом подстановки (методом замены переменной).
| 1. | 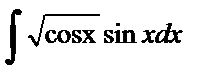 . . | 8. | 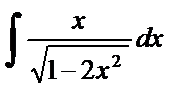 . . |
| 2. | 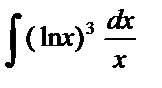 . . | 9. | 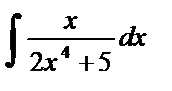 . . |
| 3. | 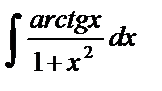 . . | 10. | 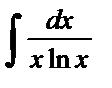 . . |
| 4. | 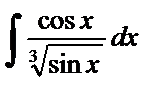 . . | ||
| 5. | 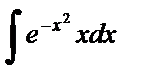 . . | ||
| 6. | 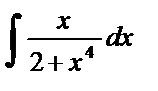 . . | ||
| 7. | 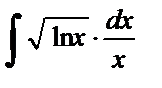 . . |
Решение типовых примеров.
Найти неопределенные интегралы: (приложения, таблица 4)
1. 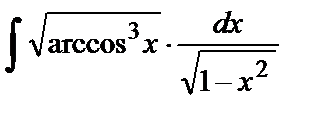 . Сделаем замену t=arccosx. Тогда
. Сделаем замену t=arccosx. Тогда 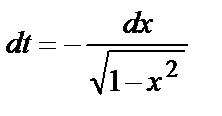 и
и 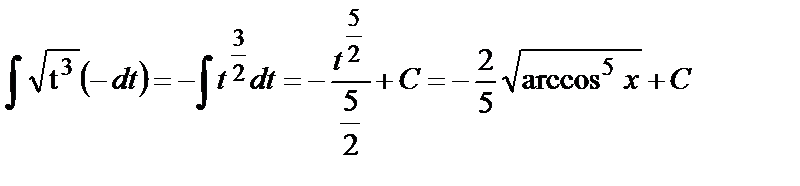 .
.
2. 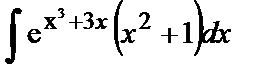 . Применим подстановку
. Применим подстановку 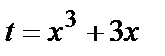 , тогда
, тогда 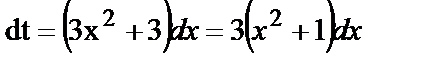 , откуда
, откуда 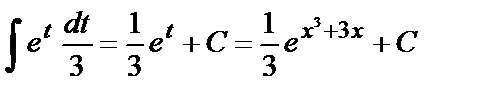 .
.
ТЕМА «НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ.
Задание №4. найти неопределенные интегралы, применяя метод интегрирования по частям.
| 1. | 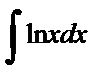 . . | 8. | 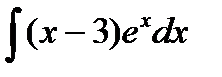 . . |
| 2. | 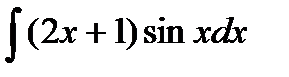 . . | 9. | 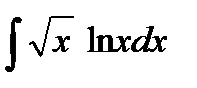 . . |
| 3. | 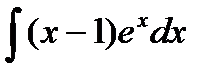 . . | 10. | 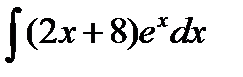 . . |
| 4. | 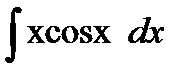 | ||
| 5. | 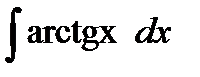 . . | ||
| 6. | 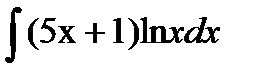 . . | ||
| 7. | 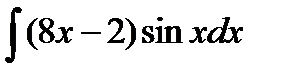 . . |
Решение типового примера.
Найти интеграл:
1. 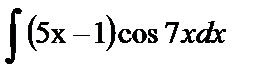 Решение: применим формулу интегрирования по частям
Решение: применим формулу интегрирования по частям 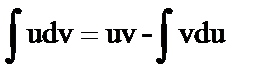 . Разбиваем подитегральное выражение на части:
. Разбиваем подитегральное выражение на части: 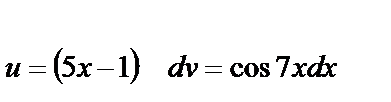 ,
,
тогда 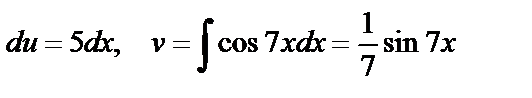 .
.
Следовательно, 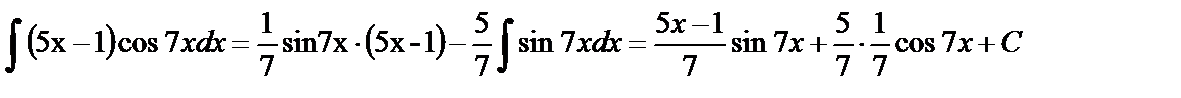 .
.
2. 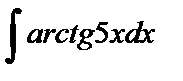 Решение: положим
Решение: положим 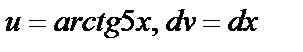 , тогда
, тогда 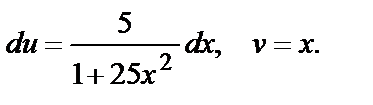
Отсюда 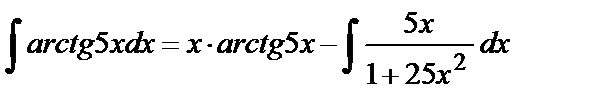 . Применяя в последнем интеграле подстановку
. Применяя в последнем интеграле подстановку 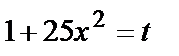 , получаем
, получаем 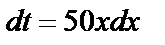 , следовательно,
, следовательно, 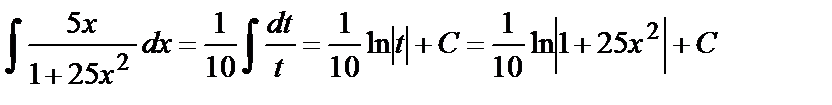 ,
,
отсюда 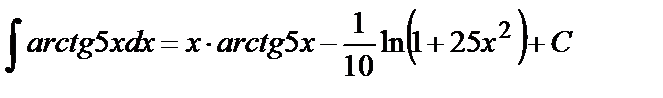 .
.
ТЕМА «КОМПЛЕКСНЫЕ ЧИСЛА»
Задание №5. Даны комплексные числа. Найти: а) их сумму; б) их разность; в) их произведение; г) их частное; д) квадрат каждого числа.
1. 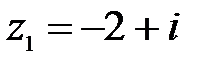 ,
, 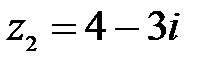 ;
;
2. 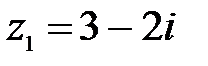 ,
, 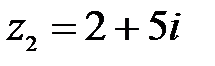 ;
;
3. 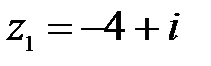 ,
, 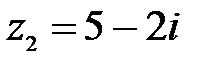 ;
;
4. 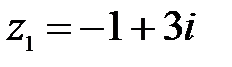 ,
, 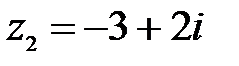 ;
;
5. 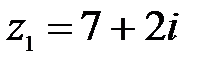 ,
, 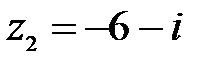 ;
;
6. 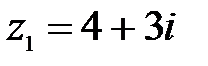 ,
, 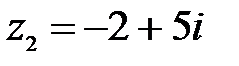 ;
;
7. 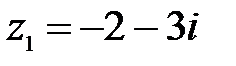 ,
, 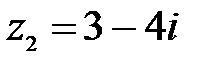 ;
;
8. 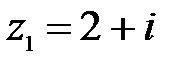 ,
, 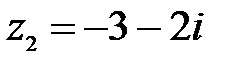 ;
;
9. 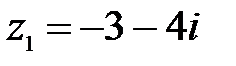 ,
, 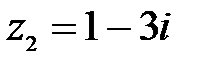 ;
;
10. 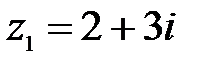 ,
, 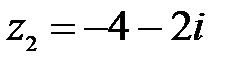 .
.
Решение типового примера
Пусть даны комплексные числа 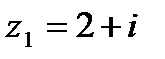 ,
, 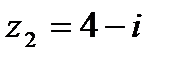 .
.
а) 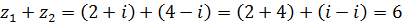 .
.
б) 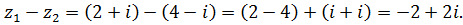
в) 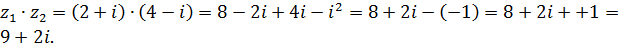
Замечание: 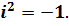
г)