Среди заданных зубчатых редукторов имеются планетарные, составные и замкнутые дифференциальные механизмы. В планетарных (W=1) и дифференциальных (W=2) передачах оси отдельных колес (сателлитов) являются подвижными. Для решения задачи необходимо разделить механизмы на части, выделив планетарные и дифференциальные, и для каждой части написать уравнение передаточного отношения, используя соответствующий метод. При решении планетарных и дифференциальных механизмов применяется метод обращения движения (метод остановки водила) – всем звеньям придается дополнительная угловая скорость (-ωH) в результате чего получается обычный механизм с неподвижными осями колес, так как водило Н будет иметь скорость ωH-ωH=0. Общее передаточное отношение сложного механизма определяется решением полученной системы уравнений. В задании входным звеном является колесо "а", выходным – звено I, поэтому искомым является передаточное отношение ia1 В рассматриваемом примере (рисунок 12) ось колес 8-8' является подвижной (8-8' – сателлиты). Они входят в зацепление с колесами 7 и 9, которые называются центральными. 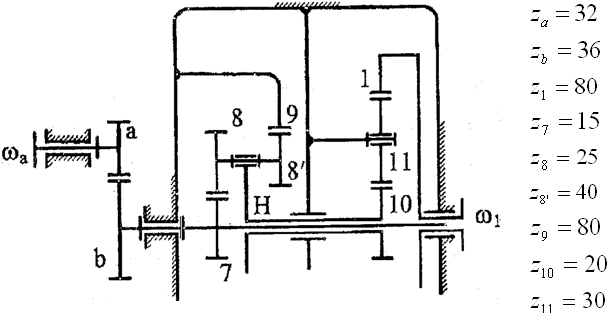 Рисунок 12 - Схема редуктора Таким образом колеса 7, 8, 8', 9 и водило Н (звено, соединяющее ось сателлитов с центральной осью) составляют планетарную передачу, а весь механизм делится на три части: – обычная зубчатая пара, 7, 8, 8', 9 – планетарная часть, 10, 11,1 – обычная (рядовая) передача. Запишем уравнения для рядовых передач: Рисунок 12 - Схема редуктора Таким образом колеса 7, 8, 8', 9 и водило Н (звено, соединяющее ось сателлитов с центральной осью) составляют планетарную передачу, а весь механизм делится на три части: – обычная зубчатая пара, 7, 8, 8', 9 – планетарная часть, 10, 11,1 – обычная (рядовая) передача. Запишем уравнения для рядовых передач: 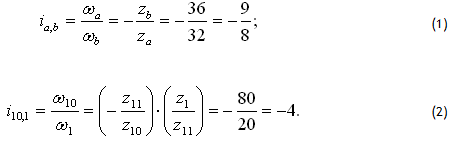 Для планетарной части, после остановки водила “Н”, колеса 7, 8, 8', 9 будут иметь скорость соответственно: ω7-ωH, ω8-ωH, ω8'-ωH, ω9-ωH а передаточное отношение между центральными колесами Для планетарной части, после остановки водила “Н”, колеса 7, 8, 8', 9 будут иметь скорость соответственно: ω7-ωH, ω8-ωH, ω8'-ωH, ω9-ωH а передаточное отношение между центральными колесами  Из (1) ωb=-8/9ωaа из (2) ω10=-4ω1 и с учетом ωb=ω7; ωH=ω10; ω9=0 подставляем в уравнение (3): Из (1) ωb=-8/9ωaа из (2) ω10=-4ω1 и с учетом ωb=ω7; ωH=ω10; ω9=0 подставляем в уравнение (3): 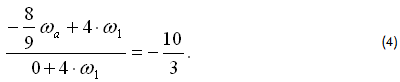 Преобразуем (4), разделив почленно числитель и знаменатель на ω1: Преобразуем (4), разделив почленно числитель и знаменатель на ω1: 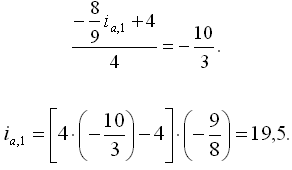 |
Расчет зубчатых колес
Геометрический расчет пары зубчатых колес, нарезанных стандартным инструментом реечного типа Расчет начинают с определения коэффициентов смещения Х1 и Х2 с помощью блокирующего контура [7]. Если по заданию дается угол зацепления передачи αw, то необходимо вначале определить ΣX=X1+X2 пользуясь формулой по п. 2.2.1. Каждому значению ΣX на блокирующем контуре соответствует прямая, направленная слева вниз направо и пересекающая оси координат под углом 450. Выбираем на этой прямой точку, удовлетворяющую дополнительным условиям. В тех случаях, когда по условию задачи необходимо выбирать наибольшую или наименьшую ΣX, тогда эту прямую под углом 450 перемещают соответственно вверх или вниз (насколько позволяют границы блокирующего контура). Стандартный инструмент реечного типа имеет следующие параметры, значения которых входят в расчетные формулы: α=200 - угол профиля исходного контура; h*a=1,0 - коэффициент высоты головки зуба; c* - коэффициент радиального зазора; h*k=0,25 - коэффициент высоты скругленного участка. Формулы для геометрического расчета: 2.2.1 Эвольвентный угол, через который определяется и угол зацепления αw: 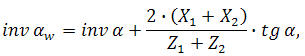 где αw - определяется по таблице. 2.2.2 Межосевое расстояние: где αw - определяется по таблице. 2.2.2 Межосевое расстояние: 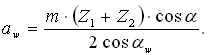 2.2.3 Диаметры делительных окружностей: di = m ⋅ Zi . 2.2.4 Диаметры начальных окружностей: 2.2.3 Диаметры делительных окружностей: di = m ⋅ Zi . 2.2.4 Диаметры начальных окружностей: 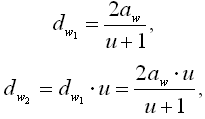 где u=z2/z1 - передаточное число. 2.2.5 Диаметры основных окружностей: где u=z2/z1 - передаточное число. 2.2.5 Диаметры основных окружностей: 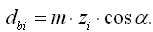 2.2.6 Диаметры окружностей впадин: 2.2.6 Диаметры окружностей впадин: 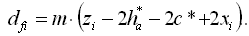 2.2.7 Диаметры окружностей вершин: 2.2.7 Диаметры окружностей вершин: 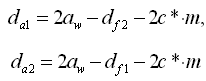 2.2.8 Шаг по делительной окружности: P=π⋅m 2.2.9 Шаг по основной окружности: Pb=P⋅cosα 2.2.10 Толщина зуба по дуге делительной окружности: 2.2.8 Шаг по делительной окружности: P=π⋅m 2.2.9 Шаг по основной окружности: Pb=P⋅cosα 2.2.10 Толщина зуба по дуге делительной окружности: 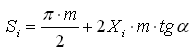 2.2.11 Эвольвентный угол при вершине определяется по таблице, через угол профиля на окружности вершин αai 2.2.11 Эвольвентный угол при вершине определяется по таблице, через угол профиля на окружности вершин αai 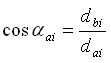 2.2.12 Толщина зуба на окружности вершин: 2.2.12 Толщина зуба на окружности вершин: 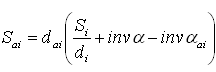 2.2.13 Коэффициент перекрытия: 2.2.13 Коэффициент перекрытия: 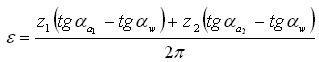 2.2.14 Угол αpi в нижней точке активного профиля зуба: 2.2.14 Угол αpi в нижней точке активного профиля зуба: 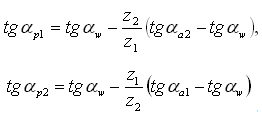 2.2.15 Угол αli в граничной точке профиля зуба: 2.2.15 Угол αli в граничной точке профиля зуба: 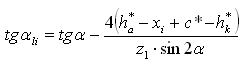 Делаем проверку геометрических показателей качества зацепления: а) проверка на отсутствие интерференции: tgαpi ≥ tgαli; б) проверка на отсутствие подрезания: tgαli ≥ 0; в) проверка на отсутствие заострения: Sai ≥ [Sa], где [Sa] берется в соответствии с заданием (0,25m или 0,4m); г) проверка коэффициента перекрытия: ε ≥ 1,2. Делаем проверку геометрических показателей качества зацепления: а) проверка на отсутствие интерференции: tgαpi ≥ tgαli; б) проверка на отсутствие подрезания: tgαli ≥ 0; в) проверка на отсутствие заострения: Sai ≥ [Sa], где [Sa] берется в соответствии с заданием (0,25m или 0,4m); г) проверка коэффициента перекрытия: ε ≥ 1,2. |
Наши рекомендации
 Рисунок 12 - Схема редуктора Таким образом колеса 7, 8, 8', 9 и водило Н (звено, соединяющее ось сателлитов с центральной осью) составляют планетарную передачу, а весь механизм делится на три части: – обычная зубчатая пара, 7, 8, 8', 9 – планетарная часть, 10, 11,1 – обычная (рядовая) передача. Запишем уравнения для рядовых передач:
Рисунок 12 - Схема редуктора Таким образом колеса 7, 8, 8', 9 и водило Н (звено, соединяющее ось сателлитов с центральной осью) составляют планетарную передачу, а весь механизм делится на три части: – обычная зубчатая пара, 7, 8, 8', 9 – планетарная часть, 10, 11,1 – обычная (рядовая) передача. Запишем уравнения для рядовых передач: 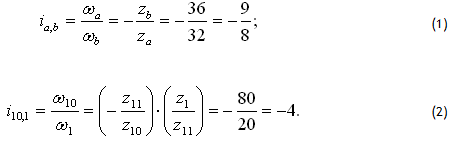 Для планетарной части, после остановки водила “Н”, колеса 7, 8, 8', 9 будут иметь скорость соответственно: ω7-ωH, ω8-ωH, ω8'-ωH, ω9-ωH а передаточное отношение между центральными колесами
Для планетарной части, после остановки водила “Н”, колеса 7, 8, 8', 9 будут иметь скорость соответственно: ω7-ωH, ω8-ωH, ω8'-ωH, ω9-ωH а передаточное отношение между центральными колесами  Из (1) ωb=-8/9ωaа из (2) ω10=-4ω1 и с учетом ωb=ω7; ωH=ω10; ω9=0 подставляем в уравнение (3):
Из (1) ωb=-8/9ωaа из (2) ω10=-4ω1 и с учетом ωb=ω7; ωH=ω10; ω9=0 подставляем в уравнение (3): 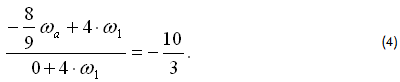 Преобразуем (4), разделив почленно числитель и знаменатель на ω1:
Преобразуем (4), разделив почленно числитель и знаменатель на ω1: 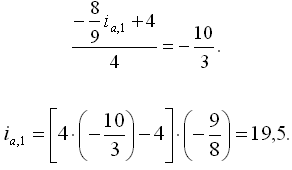
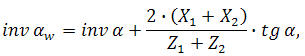 где αw - определяется по таблице. 2.2.2 Межосевое расстояние:
где αw - определяется по таблице. 2.2.2 Межосевое расстояние: 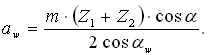 2.2.3 Диаметры делительных окружностей: di = m ⋅ Zi . 2.2.4 Диаметры начальных окружностей:
2.2.3 Диаметры делительных окружностей: di = m ⋅ Zi . 2.2.4 Диаметры начальных окружностей: 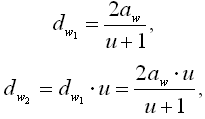 где u=z2/z1 - передаточное число. 2.2.5 Диаметры основных окружностей:
где u=z2/z1 - передаточное число. 2.2.5 Диаметры основных окружностей: 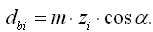 2.2.6 Диаметры окружностей впадин:
2.2.6 Диаметры окружностей впадин: 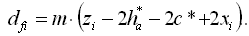 2.2.7 Диаметры окружностей вершин:
2.2.7 Диаметры окружностей вершин: 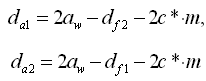 2.2.8 Шаг по делительной окружности: P=π⋅m 2.2.9 Шаг по основной окружности: Pb=P⋅cosα 2.2.10 Толщина зуба по дуге делительной окружности:
2.2.8 Шаг по делительной окружности: P=π⋅m 2.2.9 Шаг по основной окружности: Pb=P⋅cosα 2.2.10 Толщина зуба по дуге делительной окружности: 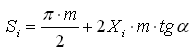 2.2.11 Эвольвентный угол при вершине определяется по таблице, через угол профиля на окружности вершин αai
2.2.11 Эвольвентный угол при вершине определяется по таблице, через угол профиля на окружности вершин αai 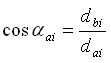 2.2.12 Толщина зуба на окружности вершин:
2.2.12 Толщина зуба на окружности вершин: 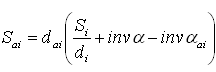 2.2.13 Коэффициент перекрытия:
2.2.13 Коэффициент перекрытия: 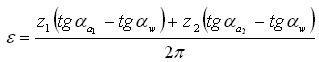 2.2.14 Угол αpi в нижней точке активного профиля зуба:
2.2.14 Угол αpi в нижней точке активного профиля зуба: 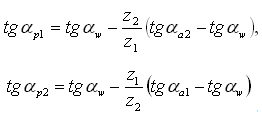 2.2.15 Угол αli в граничной точке профиля зуба:
2.2.15 Угол αli в граничной точке профиля зуба: 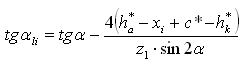 Делаем проверку геометрических показателей качества зацепления: а) проверка на отсутствие интерференции: tgαpi ≥ tgαli; б) проверка на отсутствие подрезания: tgαli ≥ 0; в) проверка на отсутствие заострения: Sai ≥ [Sa], где [Sa] берется в соответствии с заданием (0,25m или 0,4m); г) проверка коэффициента перекрытия: ε ≥ 1,2.
Делаем проверку геометрических показателей качества зацепления: а) проверка на отсутствие интерференции: tgαpi ≥ tgαli; б) проверка на отсутствие подрезания: tgαli ≥ 0; в) проверка на отсутствие заострения: Sai ≥ [Sa], где [Sa] берется в соответствии с заданием (0,25m или 0,4m); г) проверка коэффициента перекрытия: ε ≥ 1,2. 