Тема 2.Растяжение и сжатие

ВВЕДЕНИЕ

Сопротивление материалов – учебная дисциплина о прочности, жёсткости и устойчивости элементов несущих конструкций. Неправильный расчёт самой незначительной детали может повлечь за собой очень тяжёлые последствия – привести к разрушению конструкции в целом. При проведении расчётов необходимо стремиться к сочетанию надёжности работы конструкции с её дешевизной, добиваться наибольшей прочности при наименьшем расходе материала.

Сопротивление материалов – одна из сложных дисциплин, изучаемых в высших технических учебных заведениях; занятия по этому курсу должны обязательно сопровождаться составлением конспекта и решением задач. Если при решении задач возникают затруднения, следует воспользоваться имеющимися в задачниках указаниями и примерами, но совершенно необходимо научиться самостоятельно решать задачи и делать выводы формул. При этом нужно обращать внимание на физическую сущность явления и на допущения и ограничения, которые делаются в процессе выводов. Необходимо хорошо разбираться в чертежах, которыми сопровождаются выводы формул. После изучения каждой темы следует ответить на вопросы для самопроверки.

Студенты-заочники изучают"Сопротивление материалов" в пятом и шестом семестрах. Соответственно числу семестров весь курс сопротивления материалов поделен на две части. В пятом семестре изучаются цели, задачи, основные гипотезы сопротивления материалов, геометрические характеристики плоских сечений и простые виды деформаций прямого бруса (растяжение-сжатие, сдвиг, кручение, изгиб). В шестом семестре – сложное сопротивление, изгиб криволинейного стержня, методы определения перемещений, устойчивость, удар, статически неопределимые балки.

Тема 1.Основные понятия

В этой теме даны основные понятия, которые необходимо хорошо усвоить. Особое внимание следует обратить на понятия деформаций и напряжений. Для определения напряжений пользуются методом сечений. Сущность его заключается в том, что твёрдое тело, находящееся в равновесии, разрезают (мысленно) на две части, отбрасывают одну из частей, заменяют влияние отброшенной части внутренними силами и составляют уравнения равновесия для оставшейся части, на которую действуют приложенные к ней внешние силы и внутренние силы, распределённые по сделанному сечению.

Литература: [4, гл. 1]; [5, гл. 1]; [7, гл. 1].

Вопросы для самопроверки

1. Какие деформации называют упругими?

2. Какие деформации называют остаточными (пластическими)?

3. Что называется напряжением в точке в данном сечении?

4. Какое напряжение называется нормальным?

5. Какое напряжение называется касательным?

6. В чём сущность метода сечений?

Тема 2.Растяжение и сжатие

Рассматриваются простые случаи воздействия сил на стержень и предложен ряд вопросов (механические свойства материалов, выбор допускаемых напряжений, статически неопределимые задачи), встречающихся в других разделах курса.

Обратите внимание на то, что механические характеристики материала (предел пропорциональности, предел упругости, предел текучести, предел прочности) находят путём деления соответствующей нагрузки на первоначальнуюплощадь поперечного сечения. Таким образом, получают условные напряжения, а не истинные; для вычисления последних надо делить нагрузки на действительную площадь поперечного сечения, которая изменяется при опыте. Зная истинные напряжения, можно построить так называемую истинную диаграмму растяжения, которая точнее характеризует свойства материала, чем условная диаграмма. Пользуясь формулами, основанными на законе Гука, надо учитывать, что этот закон справедлив только до предела пропорциональности. Нельзя, например, напряжение для мягкой стали при 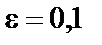вычислять по формуле 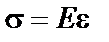, так как тогда получается, что 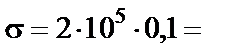20 000 МПа, в то время как при 400 МПа материал уже разрушается.

При решении статически неопределимых задач обратите внимание на то, что усилия в стержнях статически неопределимой системы зависят от площадей поперечных сечений А и от модулей упругости E, тогда как в статически определимой системе величины А и E не влияют на распределение усилий.

Способ расчёта по допускаемым нагрузкам для статически определимых систем даёт те же результаты, что и способ расчёта по допускаемым напряжениям, но для статически неопределимых систем он позволяет вскрыть дополнительные резервы прочности, повысить несущую способность конструкции и указывает на возможность более экономного расходования материала.

Следует обратить внимание на весьма важные понятия: предел прочности, допускаемое напряжение и коэффициент запаса прочности.

После изучения этой темы можно решать задачи 4, 5, включенные в контрольные работы.

Литература: [4, гл. 3]; [5, гл. 2]; [6, гл. 1, задачи: 1, 3, 16, 19, 20, 26, 30, 37, 38, 55, 59, 66, 80, 84, 88, 93, 102, 118]; [7, гл. 2].

Вопросы для самопроверки

7. Как строится диаграмма растяжения?

8. Что называется пределом пропорциональности?

9. Что называется пределом упругости?

10. Что называется пределом текучести?

11. Что называется пределом прочности?

12. Как формулируется закон Гука?

13. Что называется модулем упругости?

14. Что называется коэффициентом поперечной деформации?

15. Как найти работу растягивающей силы по диаграмме растяжения?

16. Что называется удельной работой деформации?

17. Что называется истинным пределом прочности?

18. В чём разница между пластичными и хрупкими материалами?

19. В каких местах возникает концентрация напряжений?

20. Какие задачи называют статически неопределимыми? Каков общий порядок их решения?

21. Как находят напряжения при изменении температуры?

22. Как находят удлинение стержня, растягиваемого собственным весом?

23. От каких факторов зависит запас прочности?

24. Что называется коэффициентом запаса прочности?

25. Как формулируется условие прочности?

Тема 3.Сдвиг

Касательные напряжения на двух взаимно перпендикулярных площадках равны между собой. Этот закон называется законом парности касательных напряжений. При изучении деформаций обратите внимание на то, что одна из диагоналей выделенного элемента, по граням которого действуют касательные напряжения, удлиняется, а другая укорачивается; таким образом, явления растяжения-сжатия и сдвига нельзя рассматривать изолированно друг от друга. Формулу закона Гука при сдвиге 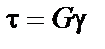легко запомнить ввиду полной аналогии ее с формулой закона Гука при растяжении-сжатии 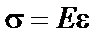. Внимательно изучите вопрос о выборе допускаемых напряжений при сдвиге.

Обратите внимание на то, что расчёты заклёпок, сварных соединений и врубок являются условными и что срез всегда осложнён наличием других напряжений, которыми для упрощения расчётов обычно пренебрегают. Надо уметь показывать на чертежах площадки, на которых возникают напряжения среза, смятия и скалывания.

Литература: [5, гл. 4]; [6, гл. 3, задачи: 2, 7, 21, 24, 27, 32];[7, гл. 4].

Вопросы для самопроверки

26. Что называется абсолютным и относительным сдвигом?

27. Как формулируется закон Гука при сдвиге?

28. Какой модуль упругости больше: E или G?

29. Как находят условную площадь смятия заклёпки?

30. По какому сечению в заклёпочном соединении проводят проверку листов на разрыв?

31. Как рассчитывают стыковые, торцовые и фланговые швы?

Тема4.Кручение

В случае центрального растяжения-сжатия нормальные напряжения распределяются в поперечном сечении стержня равномерно. При расчёте на срез обычно полагают, что касательные напряжения также распределяются равномерно. В случае кручения круглого стержня касательные напряжения в поперечном сечении распределяются неравномерно, изменяясь по линейному закону от нуля на оси до максимального значения у поверхности стержня. В связи с этим и возникла мысль о замене сплошного вала полым, материал сечения которого находится в более напряжённой зоне и используется рациональнее.

Обратите внимание на то, как используется закон парности касательных напряжений для установления напряжения t в точках контура прямоугольного поперечного сечения стержня. Наибольшее напряжение в таком сечении возникает в точках контура, ближе всего расположенных к оси кручения. После изучения этой темы можно решать задачу 6.

Литература: [4, гл. 8]; [5, гл. 6]; [6, гл. 4, задачи: 1, 9, 14, 18, 24, 32, 38, 48, 60, 63]; [7, гл. 7].

Вопросы для самопроверки

32. Как рассчитывают стыковые, торцовые и фланговые швы?

33. Какие напряжения возникают в поперечном сечении круглого стержня при кручении? Как находят их значения в произвольной точке поперечного сечения?

34. Возникают ли при кручении нормальные напряжения?

35. Чему равен полярный момент инерции круглого сечения?

36. Что называется моментом сопротивления при кручении?

37. Чему равен момент сопротивления кольцевого сечения? Почему нельзя сказать, что он равен разности моментов сопротивления наружного и внутреннего кругов?

38. Как вычисляют момент, передаваемый шкивом, по мощности и числу оборотов?

39. Как находят углы закручивания?

40. Как производят расчёт вала на прочность?

41. Как производят расчёт вала на жёсткость?

42. Как находят максимальные напряжения при кручении стержня прямоугольного сечения?

43. Как вычисляют напряжения в пружинах?

44. Как определяют деформации пружин?