Каждый элемент матрицы С вычисляется по формуле
Работа 7
Краткое теоретическое введение. В практических вычислениях довольно часто приходится решать уравнения вида:
F(x)=0, (1)
где функция f(x) определена и непрерывна на некотором конечном или бесконечном интервале, а<x<b.
Если функция определяет собой многочлен, то уравнение (1) называют алгебраическим, если же в функцию f(x) входят элементарные (тригонометрические, логарифмические, показательные и т.п.) функции, то такое уравнение называют трансцендентным.
Всякое значение х*, обращающее функцию f(x) в нуль, т.е. такое, что
f(x*) 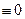 ,
,
называется корнем уравнения (1), а способ нахождения этого значения x* и есть решение уравнения (1).
Найти корни уравнения (1) точно удается лишь в частных случаях. Поэтому разработаны методы численного решения уравнений вида (1), которые позволяют отыскать приближенное значение корней этого уравнения.
При этом приходится решать две задачи:
1) отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;
2) вычисление корней с заданной точностью.
При выделении областей, в которых находятся действительные корни уравнения (1), можно воспользоваться тем, что если на концах некоторого отрезка непрерывная функция f(x) принимает значения разных знаков, то на этом отрезке уравнение (1) имеет хотя бы один корень.
Для выделения областей, содержащих один и только один корень, можно воспользоваться, например, графическим способом.
Для решения второй задачи существуют многочисленные методы. Рассмотрим три метода: метод итераций, метод Ньютона и метод половинного деления.
Будем считать, что нам известен отрезок α<x<β, внутри которого существует и располагается один и только один корень уравнения (1).
Задача состоит в нахождении этого корня.
Метод итераций. Уравнение (1) представим в виде
х=φ(х), (2)
что всегда можно сделать и притом многими способами. Например, можно выделить из уравнения (1) х, остальное перенести в правую часть (это будет φ(х)). Или умножить левую и правую части (1) на произвольную константу λ и прибавить к левой и правой частям х, т.е представить (1) в виде
х=х+λf(x).
При этом φ(х)=х+λf(х).
Выберем на отрезке [α,β] произвольную точку х0 – нулевое приближение, и примем в качестве следующего приближения
х1=φ(х0),
далее
х2=φ(х1),
и вообще пусть хn получается из хn-1 по формуле
хn=φ(хn-1). (3)
Этот процесс последовательного вычисления чисел хn (n=1,2,3,…) по формуле (3) называется методом итераций.
Если на отрезке [α,β], содержится корень х=х* уравнения (2), а также его последовательные приближения х1,х2,…хn,…, вычисленные по методу итераций, выполнено условие
|φ(х)≤q<1,
то процесс итераций сходится, т.е. увеличивая n можно получить приближение, сколь угодно мало отличающегося от истинного значения корня х*.
Процесс итераций следует продолжать тех пор, пока для двух последовательных приближений хn-1 и хn не будет обеспечено выполнение неравенства
|хn - хn-1|≤  ε; (4)
ε; (4)
при этом всегда будет выполняться неравенство
|х* - хn|≤ε,
где ε – заданная предельная абсолютная погрешность корня х*.
Если q≤0,5, то  ≥1 и (4) можно пользоваться более простым соотношением
≥1 и (4) можно пользоваться более простым соотношением
|хn - хn-1|≤ε, (5)
при выполнении, которого также будет обеспеченна заданная точность определения корня х*.
При практическом нахождении корней по методу итераций нужно при переходе от уравнений (1) к уравнению (2) стремиться представить φ(х) так, чтобы производная φ′(х) по абсолютной величине была, возможно, меньше 1.
Метод Ньютона. Пусть уравнение f(x)=0имеет один корень на отрезке [α,β], причем f′(x) и f′′(x) определены, непрерывны и сохраняют постоянные знаки на отрезке [α,β].
Выведем формулу для последовательных приближений к корню. Уравнение касательной через точку Р0(х0,f(x0)), имеет вид:
y=f(x0)+f′(x0)(x-x0).
Пологая у=0, находим абсциссу х1 точки пересечения касательной с осью Ох:
Х1=Х0- 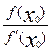 ,
,
Следующие приближения находим соответственно по формулам:
Х2=Х1-  ,
,
. . . . . . . . . . . . (6)
Хn=Хn-1- 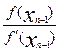 .
.
Процесс вычисления приближений прекратим при выполнении условия
|хn - хn-1|≤ 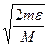 ,
,
где m - наименьшее значение |f′(x)| на отрезке [α,β]; M – наибольшее значение |f′′(x)| на отрезке [α,β].
При этом условии будет выполнено неравенство
|х* - хn|≤ε,
где ε – заданная предельная абсолютная погрешность корня х*.
Начальное приближение х0 целесообразно выбирать так, чтобы было выполнено условие f(x0) f′′(x0)>0.
Метод половинного деления. Пусть дано уравнение f(x)=0, где функция f(x) непрерывна на отрезке [α,β] и f(α)f(β)<0.
Для нахождения корня уравнения (1), принадлежащего отрезку [α,β], делим отрезок пополам, т.е. выбираем начальное приближение равным х0=(α+β)/2. Если f(x0)=0, то x0 является корнем уравнения. Если f(x0)≠0, то выбираем тот из отрезков [α,x0] или [x0,β], на концах которого функция f(x) имеет противоположные знаки. Полученный отрезок делим пополам и проводим то же рассмотрение и т.д.
Процесс деления отрезков пополам проводим до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше наперед заданного числа ε.
| Уравнение | Отрезок, содержащий корень | Метод численного решения | Приближенное значение корня | |
3sin 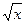 +0,35х – 3,8=0 +0,35х – 3,8=0 | [2;3] | Итераций | 2,2985 | |
| – 0,25х3+х – 1,2502=0 | [0;2] | Ньютона | 1,0001 | |
Х+ 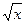 + + 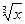 – 2,5 =0 – 2,5 =0 | [0,4;1] | Половинного деления | 0,7376 | |
х –  =0 =0 | [0;0,85] | Итераций | 0,2624 | |
| 0,1х2 – х lnx=0 | [1;2] | Ньютона | 1,1183 | |
tg x – 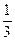 tg3 x + tg3 x + 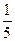 tg5 x – tg5 x –  =0 =0 | [0;0,8] | Половинного деления | 0,3333 | |
arcos x –  =0 =0 | [0;1] | Итераций | 0,5629 | |
| 3x – 4 ln x – 5 =0 | [2;4] | Ньютона | 3,2300 | |
cos 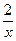 – 2 sin – 2 sin 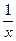 + + 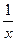 = 0 = 0 | [1;2] | Половинного деления | 1,8756 | |
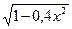 – arcsinx = 0 – arcsinx = 0 | [0;1] | Итераций | 0,7672 | |
| ex – e -x – 2 = 0 | [0;1] | Ньютона | 0,8814 | |
| Sin(lnx) – cos(lnx) + 2lnx = 0 | [1;3] | Половинного деления | 1,3749 | |
x – 2 + sin 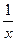 = 0 = 0 | [1,2;2] | Итераций | 1,3077 | |
| ex +lnx – 10x =0 | [3;4] | Ньютона | 3,5265 | |
Сosx – e-x 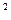 + x – 1 = 0 + x – 1 = 0 | [1;2] | Половинного деления | 1,0804 | |
| 1 – x + sinx – ln(1+x)=0 | [0;1,5] | Итераций | 1,1474 | |
| 3x – 14 + ex – e-x =0 | [1;3] | Ньютона | 2,0692 | |
 – tgx = 0 – tgx = 0 | [0;1] | Половинного деления | 0,5768 | |
| x+cos(x0,52+2)=0 | [0,5;1] | Итераций | 0,9892 | |
| 3ln2x+6lnx – 5 =0 | [1;3] | Ньютона | 1,8832 | |
| Sinx2 + cos x2 – 10x = 0 | [0;1] | Половинного деления | 0,101 | |
| x2 – ln(1+x) – 3 =0 | [2;3] | Итераций | 2,0267 | |
| 2x sinx – cosx =0 | [0,4;1] | Ньютона | 0,6533 | |
ex +  – 2 = 0 – 2 = 0 | [-1;0] | Половинного деления | –0,2877 | |
| lnx – x +1,8 = 0 | [2;3] | Итераций | 2,8459 | |
х tgx –  =0 =0 | [0,2;1] | Ньютона | 0,5472 | |
tg  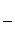 ctg ctg  +x =0 +x =0 | [1;2] | Половинно годеления | 1,0769 | |
0,4+arctg 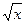 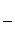 x = 0 x = 0 | [1;2] | Итераций | 1,2388 | |
 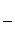 cos cos  =0 =0 | [0;1] | Ньютона | 0,4538 | |
| 0,6 3x – 2,3x – 3 =0 | [2;3] | Половинного деления | 2,42 |
Работа 8.
Вычисление определенных интегралов.
Метод трапеций.
Приближенное значение интеграла по формуле трапеций имеет вид:
 h(y0 + 2y1 + …+ 2yn-1 + yn)/2,
h(y0 + 2y1 + …+ 2yn-1 + yn)/2,
где
h= 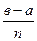 , x0=a, x1=a+h, …,xn=b.
, x0=a, x1=a+h, …,xn=b.
yi=f(xi), xi=a+ih, i=0,1, … , n.
Метод Симпсона.
Приближенное значение интеграла по формуле Симпсона имеет вид:
 h(y0 + 4y1 +2y2 +…+ 4y2n-1 + y2n)/6,
h(y0 + 4y1 +2y2 +…+ 4y2n-1 + y2n)/6,
где
h=  , x0=a, x1=a+h, …,x2n=b.
, x0=a, x1=a+h, …,x2n=b.
yi=f(xi), xi=a+ih, i=0,1, … , 2n.
| № | Подынтегральная функция | [a;b] | Метод | Точное значение первообразной |
 | [1;3,5] | Симпсона |  (lnx +1)3/2 – 2(lnx+1)1/2 + (lnx +1)3/2 – 2(lnx+1)1/2 +  | |
| tg2x + ctg2x | [π/6; π/3] | Трапеций | tgx–ctgx– 2x –tg 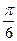 – ctg – ctg 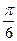 + +  | |
 | [2;3] | Симпсона | 2,3026(lnlnx – ln ln2) | |
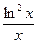 | [1;4] | Трапеций |  ln3x ln3x | |
 | [0;ln2] | Симпсона | 2  – 2arctg – 2arctg  | |
| xexsinx | [0;1] | Трапеций | (x ex (sin x– cos x) + ex cosx – 1))/2 | |
| x shx | [0;2] | Симпсона |  –- –-  | |
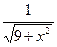 | [0;2] | Трапеций | ln(x+ 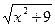 ) – ln3 ) – ln3 | |
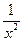 sin sin 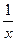  | [1;2,5] | Симпсона | cos 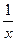 – cos1 – cos1 | |
| x arctgx | [0;  ] ] | Трапеций | 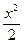 arctgx - arctgx - 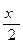 + +  arctgx arctgx | |
arcsin 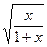 | [0;3] | Симпсона | arcsin 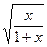 - - 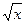 + arctg + arctg 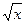 | |
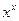 (1+lnx) (1+lnx) | [1;3] | Трапеций | 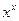 - 1 - 1 | |
 | [0;1] | Симпсона | 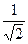 ln ln  | |
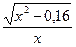 | [1;2] | Трапеций | 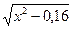 - 0,4 arccos - 0,4 arccos  - - - -  + 0,4 arccos 0,4 + 0,4 arccos 0,4 | |
| 23x | [0;1] | Симпсона |  (23x – 1) (23x – 1) | |
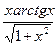 | [0;1] | Трапеций |  arctg x – ln(x+ arctg x – ln(x+  ) ) | |
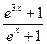 | [0;2] | Симпсона | 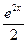 - ex + x + 0,5 - ex + x + 0,5 | |
| sin2x | [0;  ] ] | Трапеций |  - -  sin 2x sin 2x | |
x2 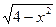 | [0;1,99] | Симпсона | 2arcsin  - -  sin(4 arcsin sin(4 arcsin  ) ) | |
| ex cos2 x | [0;π] | Трапеций |  (1+ (1+ 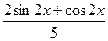 ) – 0,6 ) – 0,6 | |
| (x lnx)2 | [1;e] | Симпсона | 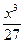 (9 ln2x – 6 lnx + 2) - (9 ln2x – 6 lnx + 2) - 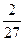 | |
Arcsin 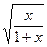 | [0;3] | Трапеций | x arcsin 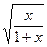 - - 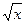 + arctg + arctg 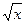 | |
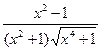 | [0;1] | Симпсона | -  arcsin( arcsin( 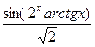 ) ) | |
| sinx ln(tgx) | [1;1,5] | Симпсона | ln(tg 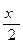 ) – (cosx)(ln(tgx)) – lntg0,5+ +(cos1) lntg1 ) – (cosx)(ln(tgx)) – lntg0,5+ +(cos1) lntg1 | |
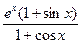 | [0;1,5] | Симпсона | ex tg  | |
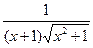 | [0;3/4] | Трапеций | 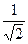 ( ln ( ln 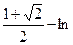 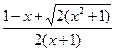 ) ) | |
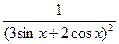 | [0;1] | Симпсона | 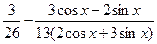 | |
28  |  | [1;2] | Трапеций |  |
 | [1;2] | Симпсона |  | |
 | [1;2] | Трапеций | 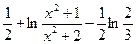 |
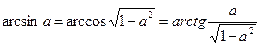


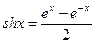

Работа 9
При программировании различных задач довольно часто возникают ситуации, когда те или иные однотипные вычисления встречаются несколько раз в одной и той же программе, либо повторяются в различных задачах. В таких случаях целесообразно алгоритм указанных вычислений один раз запрограммировать в общем виде, т.е. описать как подпрограмму, и по мере надобности использовать, т.е. производить обращение к подпрограмме.
1. Заданы четыре вектора  ,
, 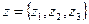 и
и  . Логической переменной а присвоить значение TRUE, если скалярное произведение векторов x и у больше скалярного произведения векторов z и p, и значение FALSE в противном случае.
. Логической переменной а присвоить значение TRUE, если скалярное произведение векторов x и у больше скалярного произведения векторов z и p, и значение FALSE в противном случае.
Вычисление скалярного произведения оформить в виде процедуры.
2. Решить уравнение dx=c, где d – длина вектора 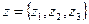 и с – длина вектора
и с – длина вектора  .
.
Вычисление длины вектора оформить в виде функции.
3. Заданы две матрицы
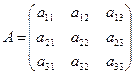 , и
, и  .
.
Проверить, является ли произведение этих матриц перестановочным, т.е проверить равенство AB=BA. В случае положительного ответа напечатать «AB=BA», иначе напечатать «ПРОИЗВЕДЕНИЕ НЕПЕРЕСТАНОВОЧНО».
Вычисление произведения двух матриц оформить в виде функции.
4. Заданы два вектора  и
и  . Логической переменной а присвоить значение TRUE, если длина векторов x больше длины вектора у, и значение FALSE в противном случае.
. Логической переменной а присвоить значение TRUE, если длина векторов x больше длины вектора у, и значение FALSE в противном случае.
Вычисление длины вектора оформить в виде функции.
5. Заданы два вектора  и
и  .Определить угол φ между векторами х и у по формуле
.Определить угол φ между векторами х и у по формуле
 .
.
Вычисление скалярного произведения оформить в виде функции.
6. Заданы две матрицы
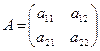 ,
,  .
.
Выяснить и напечатать, сколько из них являются симметрическими (нуль, одна или две). Матрица называется симметрической, если транспонированная матрица равна исходной.
Транспонирование матрицы оформить в виде функции.
7. Заданы два . массива  и
и 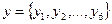 . Переменной S присвоить значение -1, если максимальный элемент массива х больше максимального элемента массива у; 0, если максимальные элементы массивов х и у равны; 1, если максимальный элемент массива х меньше максимального элемента массива у.
. Переменной S присвоить значение -1, если максимальный элемент массива х больше максимального элемента массива у; 0, если максимальные элементы массивов х и у равны; 1, если максимальный элемент массива х меньше максимального элемента массива у.
Поиск максимального элемента массива оформить в виде функции.
8. Четыре точки заданы своими координатами  ,
, 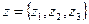 и
и  .Выяснить какие из них находятся на максимальном расстоянии друг от друга, и вывести значение этого расстояния.
.Выяснить какие из них находятся на максимальном расстоянии друг от друга, и вывести значение этого расстояния.
Вычисление расстояния между точками оформить в виде функции.
9. Четыре точки заданы своими координатами  ,
, 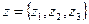 и
и  . Выяснить какие из них находятся на минимальном расстоянии друг от друга, и вывести значение этого расстояния.
. Выяснить какие из них находятся на минимальном расстоянии друг от друга, и вывести значение этого расстояния.
Вычисление расстояния между точками оформить в виде функции.
10. Заданы две матрицы
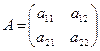 ,
, 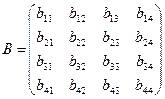 .
.
Построить таблицу функции у=сх2+d при х, меняющемся от 0 до 1 с шагом 0,1, где с есть след матрицы А, d есть след матрицы В. Следом матрицы называется сумма элементов главной диагонали.
Вычисление следа матрицы оформить в виде функции.
11. Заданы три массива  , и
, и  . Упорядочить по возрастанию три числа а,в и с, где а – минимальный элемент массива х, в – минимальный элемент массива у, а с минимальный элемент массива р.
. Упорядочить по возрастанию три числа а,в и с, где а – минимальный элемент массива х, в – минимальный элемент массива у, а с минимальный элемент массива р.
Поиск минимального элемента оформить в виде функции.
12. Заданы два вектора 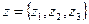 ,
,  и матрица
и матрица
 .
.
Найти сумму двух векторов с и d, где вектор с есть произведение вектора z на матрицу А, а вектор d – произведение вектора р на матрицу А.
Вычисление произведения вектора на матрицу оформить в виде функции.
13. Заданы три матрицы
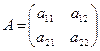 ,
,  ,
, 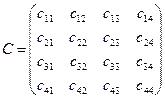 .
.
Найти минимальное из трех чисел х, у и z, где х есть след матрицы А, у – след матрицы В, z – след матрицы С. Следом матрицы называется сумма элементов главной диагонали.
Вычисление следа оформить в виде функции.
14. Заданы стороны двух треугольников: ABC (стороны a, b, c) и PLF (стороны p, l, f). Переменной S присвоить значение – 1, если площадь треугольника ABC меньше или равна площади треугольника PLF, и значение 1, если площадь треугольника ABC больше площади треугольника PLF.
Вычисление площади треугольника оформить в виде процедуры.
15. Построить таблицу функции z=sh(x+y), где х меняется от 1 до 2 с шагом 0,2; у меняется от 2 до 3 с шагом 0,1. Гиперболический синус вычисляется по формуле
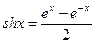 .
.
Вычисление гиперболического синуса оформить в виде процедуры.
16. Заданы стороны двух треугольников: ABC (стороны a, b, c) и PLF (стороны p, l, f). Найти сумму и разность площадей треугольников ABC и PLF.
Вычисление площади треугольника оформить в виде функции.
17. Построить таблицу функции z=сh(x2+y2), где х меняется от 3 до 4 с шагом 0,1; у меняется от 2 до 3 с шагом 0,2. Гиперболический косинус вычисляется по формуле
 .
.
Вычисление гиперболического косинуса оформить в виде функции.
18. Задана последовательность чисел:  . Выбрать из них принадлежащие отрезку [x,y]. Из выбранных чисел образовать вектор.
. Выбрать из них принадлежащие отрезку [x,y]. Из выбранных чисел образовать вектор.
Проверку на принадлежность числа отрезку оформить в виде функции.
19. Четыре точки заданы своими координатами 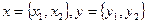 ,
, 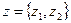 и
и  . Выяснить и напечатать, сколько из них принадлежат полосе, аналитически заданной неравенствами:
. Выяснить и напечатать, сколько из них принадлежат полосе, аналитически заданной неравенствами:
f<Ma1+Na2<r.
Проверку на принадлежность точки полосе оформить в виде функции.
20. Три точки заданы своими декартовыми координатами  ,
, 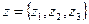 . Выяснить и напечатать полярные координаты этих точек. При выдаче на печать координаты точек упорядочить по возрастанию полярного радиуса ρ, Полярный радиус ρ и полярный угол φ вычисляются по следующим формулам:
. Выяснить и напечатать полярные координаты этих точек. При выдаче на печать координаты точек упорядочить по возрастанию полярного радиуса ρ, Полярный радиус ρ и полярный угол φ вычисляются по следующим формулам:
 ,
, 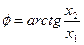 .
.
Перевод в полярные координаты оформить в виде процедуры.
21. Три точки заданы своими декартовыми координатами  ,
, 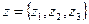 . Выдать на печать координаты этих точек по возрастанию угла между осью абсцисс и лучом, соединяющим начало координат с соответствующей точкой.
. Выдать на печать координаты этих точек по возрастанию угла между осью абсцисс и лучом, соединяющим начало координат с соответствующей точкой.
Вычисление угла между осью абсцисс и лучом, соединяющим начало координат с точкой, оформить в виде функции.
22. Заданы три матрицы
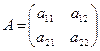 ,
,  ,
, 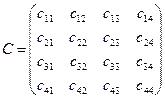 .
.
Упорядочить по убыванию три числа x, y и z, где х есть максимальный элемент матрицы А, у – максимальный элемент матрицы В, а z – максимальный элемент матрицы С.
Поиск максимального элемента оформить в виде функции.
23. Заданы две матрицы
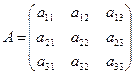 , и
, и  .
.
Найти след матрицы, равной произведению AB, и след матрицы, равной произведению BA. Следом матрицы называется сумма элементов главной диагонали.
Вычисление произведения двух матриц оформить в виде процедуры.
24. Три точки заданы своими декартовыми координатами  ,
, 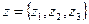 . Выдать на печать координаты точки, для которой угол между осью абсцисс и лучом, соединяющим начало координат с точкой, минимальный.
. Выдать на печать координаты точки, для которой угол между осью абсцисс и лучом, соединяющим начало координат с точкой, минимальный.
Вычисление угла между осью абсцисс и лучом, соединяющим начало координат с точкой, оформить в виде процедуры.
25. Заданы три матрицы:
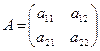 ,
,  ,
, 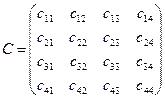 .
.
Решить квадратное уравнение px2+dx+r=0, где p есть минимальный элемент матрицы А, d – минимальный элемент матрицы B, r – минимальный элемент матрицы С.
Поиск минимального элемента оформить в виде функции.
26. Заданы три квадратных уравнения. Найти минимальное значение среди корней этих уравнений. В случае комплексных корней принять за корни действительную часть.
Решение квадратного уравнения оформить в виде функции.
27. Заданы три матрицы:
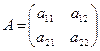 ,
,  ,
, 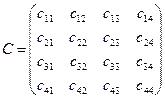 .
.
Найти длину вектора х={x1,x2,x3}, где х1 есть сумма элементов матрицы А, х2 – сумма элементов матрицы В, х3 – сумма элементов матрицы С.
Вычисление суммы элементов матрицы оформить в виде функции.
28. Даны три вектора  ,
, 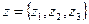 . Построить матрицу А, строками которой являются соответственно векторы x, y, z, упорядоченные в порядке возрастания.
. Построить матрицу А, строками которой являются соответственно векторы x, y, z, упорядоченные в порядке возрастания.
Упорядочение вектора по возрастанию оформить в виде функции.
29. Заданы три матрицы
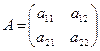 ,
,  ,
, 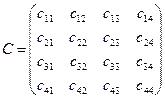 .
.
Упорядочить по возрастанию три числа x, y и z, где х есть минимальный элемент матрицы А, у – минимальный элемент матрицы В, а z – минимальный элемент матрицы С.
Поиск минимального элемента оформить в виде функции.
30. Заданы три массива  , и
, и  . Упорядочить по убыванию три числа а,в и с, где а – максимальный элемент массива х, в – максимальный элемент массива у, а с максимальный элемент массива р.
. Упорядочить по убыванию три числа а,в и с, где а – максимальный элемент массива х, в – максимальный элемент массива у, а с максимальный элемент массива р.
Поиск максимального элемента оформить в виде функции.
Работа №10
Работа содержит задачи, алгоритмы, решения которых сводятся к циклам (чаще всего двойным), внутри которых могут быть разветвления.
Программа для решения задачи должна быть составлена в общем виде, т.е. не должна меняться при изменении исходных данных в пределах ограничений, указанных в постановке задачи.
Задания
1. Составить программу для вычисления элементов матрицы С= 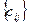 , являющейся разностью заданных матриц
, являющейся разностью заданных матриц 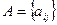 и
и 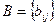 .
.
Каждый элемент матрицы С вычисляется по формуле
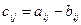 ,
, 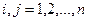 .
.
Затем вычислить компоненты вектора 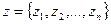 , равного произведению матрицы С=
, равного произведению матрицы С= 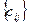 на заданный вектор
на заданный вектор  .
.
Каждая компонента вектора z вычисляется по формуле
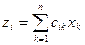 , i=1,2,…,n (n£9).
, i=1,2,…,n (n£9).
2. Составить программу для вычисления элементов матрицы С= 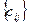 , являющейся произведением матрицы
, являющейся произведением матрицы 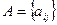 размера n*m на матрицу
размера n*m на матрицу 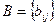 размером n*q. Каждая компонента матрицы С вычисляется по формуле
размером n*q. Каждая компонента матрицы С вычисляется по формуле 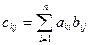 , i=1,2,…,n, j=1,2,…, q, k=1,2,…,m (n£6, q£8, m£10).
, i=1,2,…,n, j=1,2,…, q, k=1,2,…,m (n£6, q£8, m£10).
3. Составить программу для вычисления элементов вектора  , равного произведению матрицы
, равного произведению матрицы 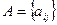 на вектор
на вектор 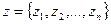 .Каждая компонента вектора х вычисляется по формуле
.Каждая компонента вектора х вычисляется по формуле
 , i=1,2,…,n ((n£8, m£9).
, i=1,2,…,n ((n£8, m£9).
4. Составить программу для вычисления элементов матрицы С= 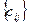 , являющейся суммой матриц
, являющейся суммой матриц 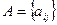 и
и 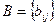 . Каждая компонента матрицы С вычисляется по формуле
. Каждая компонента матрицы С вычисляется по формуле
 , (i,j=1,2,…,n),
, (i,j=1,2,…,n),
причем матрица А задана, а элементы матрицы В вычисляются по формуле:

n=4.
5. Составить программу для нахождения наибольшего элемента матрицы С= 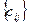 . Каждый элемент матрицы С вычисляется по формуле
. Каждый элемент матрицы С вычисляется по формуле
 , i=1,2,…,n, j=1,2,…,m.
, i=1,2,…,n, j=1,2,…,m.
Векторы x и y заданы ( n£10, m£9).
6. Составить программу для вычисления элементов вектора  , равного р-й строке матрицы
, равного р-й строке матрицы 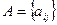 (хj=apj, j=1,2,…,m)
(хj=apj, j=1,2,…,m)  , равного q-му столбцу матрицы
, равного q-му столбцу матрицы 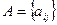 (yj=aiq, i=12,…,n), (n<7, m<9).
(yj=aiq, i=12,…,n), (n<7, m<9).
7. Составить программу для вычисления величины 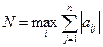 , i=1,2,…,n, где матрица
, i=1,2,…,n, где матрица 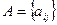 , i,j=1,2,…,n
, i,j=1,2,…,n  задана. Для решения задачи составить вектор
задана. Для решения задачи составить вектор 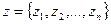 ,
,  , i=1,2,…,n, и затем найти максимальный элемент этого вектора. Это и есть N (n<7).
, i=1,2,…,n, и затем найти максимальный элемент этого вектора. Это и есть N (n<7).
8. Составить программу для нахождения наименьшей компоненты вектора  , где каждая компонента yj вычисляется по формуле
, где каждая компонента yj вычисляется по формуле
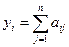 , j=1,2,…,m.
, j=1,2,…,m.
Матрица 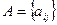 заданна. n=3, m=4.
заданна. n=3, m=4.
9. Составить программу, вычисляющую сумму ряда:


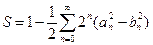 ,
,
 где a
где a  . Значения a0, и b0 заданы. Вычисление прекратить, когда будет выполнено условие
. Значения a0, и b0 заданы. Вычисление прекратить, когда будет выполнено условие 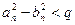
 Исходные данные
Исходные данные 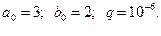
 10. Составить программу для вычисления элементов матрицы С=
10. Составить программу для вычисления элементов матрицы С= 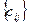 , каждый элемент которой вычисляется по формуле
, каждый элемент которой вычисляется по формуле
 (i=1,2,…,n, j=1,2,…,m).
(i=1,2,…,n, j=1,2,…,m).
n<7, m<13.
11. . Составить программу для вычисления суммы
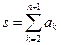 , где
, где
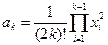 , k=2,3,…,n+1. Значения величин х1, х2,…,хn заданы (n<20).
, k=2,3,…,n+1. Значения величин х1, х2,…,хn заданы (n<20).
12. Составить программу для вычисления элементов матрицы С= 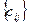 . Каждый элемент
. Каждый элемент  вычисляется по формуле
вычисляется по формуле
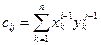 , i, j=1,2,3, где
, i, j=1,2,3, где

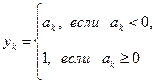
k=1,2,…,n.
Значения a1, a2,…,an заданы (n<20).
13. Составить программу для вычисления элементов вектора 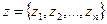 , каждая компонента которого вычисляется по формуле
, каждая компонента которого вычисляется по формуле  , где хk, yk компоненты векторов
, где хk, yk компоненты векторов  и
и  (n<10),
(n<10),
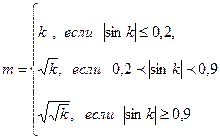
n=8.
14.Cоставить программу для вычисления матрицы с= 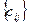 , равной произведению числа λ на матрицу а=
, равной произведению числа λ на матрицу а=  . Каждый компонент матрицы с вычисляется по формуле сij=λаij, где λ – наибольший элемент заданного вектора
. Каждый компонент матрицы с вычисляется по формуле сij=λаij, где λ – наибольший элемент заданного вектора  (n<7, m<11).
(n<7, m<11).
15. Составить программу для вычисления угла φ между векторами  и
и  , который можно определить из выражения
, который можно определить из выражения
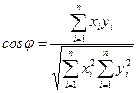 (n<20).
(n<20).
16. Составить программу для вычисления выражения
 , где α – максимальное из чисел x, y, z,
, где α – максимальное из чисел x, y, z, 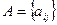 - заданная матрица.
- заданная матрица.
17.Составить программу для вычисления билинейной формы
 ,
,
где m – максимальный элемент вектора  . Матрица
. Матрица 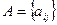 , i, j=1,2,…,n, вектор х и вектор
, i, j=1,2,…,n, вектор х и вектор  заданы (n<7).
заданы (n<7).
18. Составить программу для вычисления элементов вектора 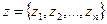 , равного произведению заданной матрицы
, равного произведению заданной матрицы 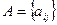 на вектор
на вектор  . Каждая компонента вектора z вычисляется по формуле
. Каждая компонента вектора z вычисляется по формуле
 , i=1,2,…,n, j=1,2,…,n.
, i=1,2,…,n, j=1,2,…,n.
Компоненты вектора х в свою очередь вычисляются по формуле
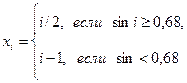
(n<9).
19. Составить программу, которая из вектора  (n<20) выделяет вектор
(n<20) выделяет вектор 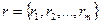 (m≤n) по правилу: компонента вектора p является компонентой вектора r, если квадратное уравнение
(m≤n) по правилу: компонента вектора p является компонентой вектора r, если квадратное уравнение
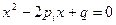
имеет вещественные и различные корни.
20. Вещественный вектор  - задан. Компоненты вектора
- задан. Компоненты вектора  вычисляются по формуле
вычисляются по формуле
 .
.
Логической  переменной а присвоить значение TRUE, если
переменной а присвоить значение TRUE, если

Принадлежит отрезку [0;1] и значение FALSE в противном случае.
21. Вещественный вектор  - задан. Осуществить циклический сдвиг компонент этого вектора:
- задан. Осуществить циклический сдвиг компонент этого вектора:
1. влево на одну позицию, т.е получить вектор 
2. вправо на две позиции, т.е. получить вектор 
22. Задана вещественная матрица 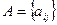 , i, j=1,2,…,n. Построить логический вектор
, i, j=1,2,…,n. Построить логический вектор 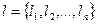 по правилу: если i строка матрицы А образует неубывающую последовательность, то
по правилу: если i строка матрицы А образует неубывающую последовательность, то  присвоить значение TRUE. В противном случае
присвоить значение TRUE. В противном случае  присвоить значение FALSE.
присвоить значение FALSE.
23. Заданы логический вектор 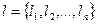 , и вещественный вектор
, и вещественный вектор  . Преобразовать вектор х по правилу: если
. Преобразовать вектор х по правилу: если  имеет значение TRUE, то хi умножить на 10, в противном случае изменить знак хi на противоположный.
имеет значение TRUE, то хi умножить на 10, в противном случае изменить знак хi на противоположный.
24. Вычислить значения компонент вектора  по формуле
по формуле
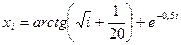 , i= 1,2,…,20/
, i= 1,2,…,20/
Логической переменной присвоить значение TRUE, если компоненты х образуют возрастающую последовательность и значение FALSE в противном случае.
25. Дана вещественная матрица 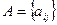 , i, j=1,2,…,n. Найти сумму элементов матрицы, расположенных в строках с отрицательным элементом на главной диагонали.
, i, j=1,2,…,n. Найти сумму элементов матрицы, расположенных в строках с отрицательным элементом на главной диагонали.
Работа 11
1. Написать программу, описывающую массив записей содержащую информацию в почтовой базе данных о подписчиках на газеты и журналы:
1. ФИО (тип сhar[10] ):
2. адрес (тип char[20]):
3. 10строк с названием газет и журналов.
Произвести поиск по фамилии.
2. Написать программу, описывающую массив записей – телефонный справочник однокурсников – и обеспечивающую ввод данных, поиск номера телефона по фамилии, подсчет и вывод списка всех абонентов по критерию «увлечение компьютерными играми». В записи о каждом однокурснике содержатся следующие сведения: фамилия, имя, телефон, хобби.
3. Написать программу, описывающую массив записей содержащую информацию в больничной базе данных о стационарных больных:
1. ФИО (тип сhar[10] ):
2. возраст (тип сhar[30]);
3. адрес (тип сhar[10]);
4. дату поступления (тип сhar[10]);
5. диагноз (тип сhar[5]).
Произвести поиск по фамилии.
4. Написать программу, описывающую массив записей содержащую информацию о хранящихся на складе товарах:
1. код товара (тип сhar[10] ):
2. наименование товара (тип сhar[8]);
3. цену (тип float);
Найти товар с наибольшей ценой.
5. Написать программу, описывающую массив записей содержащую информацию о движении электропоездов:
1. направление (тип сhar[10] ):
2. время отправления (тип floatl);
Произвести поиск по направлению.
6. Написать программу, описывающую массив записей содержащую информацию для школьной базы данных:
1. ФИО (тип сhar[10] ):
2. личный номер (тип int);
3. адрес (тип сhar[10]);
4. год рождения (int);
Произвести поиск по фамилии.
7. Написать программу, описывающую массив записей, содержащий информацию об успеваемости учащихся группы:
1. ФИО (тип сhar[10] ):
2. название предмета (тип сhar[8]);
3. оценки за две контрольные работы по трем предметам (тип int);
Программа должна обеспечивать вывод списков учащихся выполнивших первую контрольную работу по всем предметам на 5.
8. Написать программу, описывающую массив записей, содержащий информацию об успеваемости учащихся группы:
1. ФИО (тип сhar[10] ):
2. название предмета (тип сhar[10]);
3. оценки за две контрольные работы по трем предметам (тип int);
Программа должна обеспечивать вывод списков учащихся выполнивших хотя бы одну работу на 5.
9. Написать программу, описывающую массив записей, содержащий информацию об успеваемости учащихся группы:
1. ФИО (тип сhar[10] ):
2. название предмета (тип сhar[10]);
3. оценки за две контрольные работы по трем предметам (тип int);
Программа должна обеспечивать вывод списков учащихся выполнивших все работы на 4 и 5.
10. Написать программу, описывающую массив записей, содержащий информацию об успеваемости учащихся группы:
1. ФИО (тип сhar[10] ):
2. название предмета (тип сhar[10]);
3. оценки за две контрольные работы по трем предметам (тип int).
Программа должна обеспечивать вывод списков учащихся выполнивших две работы на 4 и 5.
11. Написать программу, описывающую массив записей, содержащий информацию об успеваемости учащихся группы:
1. ФИО (тип сhar[10]):
2. название предмета (тип сhar[10]);
3. оценки за две контрольные работы по трем предметам (тип int);
Программа должна обеспечивать вывод списков учащихся выполнивших все работы на 3.
12. Написать программу, описывающую массив записей, содержащий информацию об успеваемости учащихся группы:
1. ФИО (тип сhar[10] ):
2. название предмета (тип сhar[10]);
3. оценки за две контрольные работы по трем предметам (тип int);
Программа должна обеспечивать вывод списков учащихся выполнивших хотя бы одну работу на 2.
13. Написать программу, описывающую массив записей, содержащий информацию об успеваемости учащихся группы:
1. ФИО (тип сhar[10]):
2. название предмета (тип сhar[10]);
3. оценки за две контрольные работы по трем предметам (тип int);
Программа должна обеспечивать вывод списков учащихся выполнивших две контрольные работы по всем предметам на 2.
14. Написать программу, описывающую массив записей, содержащий информацию о жильцах дома, в котором будет записана следующая информация:
1. номер квартиры (тип intr):
2. ФИО предмета (тип сhar[10]);
3. возраст (тип int);
4. род занятий (тип сhar[10]).
Программа должна обеспечивать вывод квартиры с максимальным числом жильцов.
15. Написать программу, описывающую массив записей, содержащий информацию о жильцах дома, в котором будет записана следующая информация:
1. номер квартиры (тип int):
2. ФИО предмета (тип сhar[10]);
3. возраст (тип int);
4. род занятий (тип сhar[10]).
Программа должна обеспечивать поиск самого пожилого жильца.
16. Написать программу, описывающую массив записей, содержащий информацию о жильцах дома, в котором будет записана следующая информация:
1. номер квартиры (тип int):
2. ФИО предмета (тип сhar[10]);
3. возраст (тип int);
4. род занятий (тип сhar[10]).
Программа должна обеспечивать поиск самого молодого жильца.
17. Написать программу, описывающую массив записей содержащую информацию для школьной базы данных:
1. ФИО (тип сhar[10]):
2. личный номер (тип int);
3. адрес (тип сhar[10]);
4. год рождения (int);
5. адрес (тип сhar[10]).
Произвести поиск по году рождения.
18. Написать программу, описывающую массив записей содержащую информацию в больничной базе данных о стационарных больных:
1. ФИО (тип сhar[10] ):
2. возраст (тип int);
3. адрес (тип сhar[10]);
4. дату поступления (тип сhar[10]);
5. диагноз (тип сhar[10]).
Произвести поиск по дате поступления.
19. Написать программу, описывающую массив записей содержащую информацию в больничной базе данных о стационарных больных:
1. ФИО (тип сhar[10]):
2. возраст (тип int);
3. адрес (тип сhar[10]);
4. дату поступления (тип сhar[10]);
5. диагноз (тип сhar[10]);
6. лечащий врач.
Произвести поиск по фамилии лечащего врача.
20. Написать программу, описывающую массив записей содержащую информацию о движении электропоездов:
1. направление (тип сhar[10] ):
2. время отправления (тип float);
3. номеру рейса.
Произвести поиск по номеру рейса
21. Написать программу, описывающую массив записей содержащую информацию в почтовой базе данных о подписчиках на газеты и журналы:
1. ФИО (тип сhar[10] ):
2. адрес (тип сhar[10]):
3. 10строк с названием газет и журналов.
Произвести поиск и названию газеты.
22. Написать программу, описывающую массив записей содержащую информацию для школьной базы данных:
1. ФИО (тип сhar[10] ):
2. личный номер (тип int);
3. адрес (тип сhar[10]);
4. год рождения (int);
Произвести поиск учащихся заданного года рождения.
23. Написать программу, описывающую массив записей, содержащий информацию об успеваемости учащихся группы, в котором будет записана следующая информация:
1. ФИО (тип сhar[10] ):
2. название предмета (тип сhar[10]);
3. оценки за две контрольные работы по трем предметам (тип int);
Вывести название предмета, в котором меньше всего 2.
24. Написать программу, описывающую массив записей содержащую информацию в больничной базе данных о стационарных больных:
1. ФИО (тип сhar[10] ):
2. возраст (тип int);
3. адрес (тип сhar[10]);
