Силы инерции твердого тела
Главный вектор сил инерции точек тела, при любом его движении,
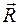ин = 
.
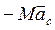То есть величина главного вектора равна произведению массы тела на ускорение центра масс его и направлен в сторону противоположную ускорению центра масс.
Рассмотрим несколько частных случаев.
1. Твердое тело движется поступательно.
При таком движении главный момент сил инерции можно не определять, а находить сразу равнодействующую этих сил.
Она равна главному вектору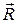 
ин =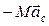 
, и приложена к точке, радиус-вектор которой 
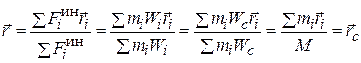, равен радиусу-вектору центра масс.
Следовательно, равнодействующая сил инерции точек тела при поступательном движении приложена к центру масс тела, как к центру параллельных сил.
2. Твердое тело вращается вокруг неподвижной оси.
Главный момент сил инерции точек тела относительно неподвижной оси вращения равен произведению момента инерции тела относительно этой оси на модуль углового ускорения
.
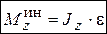Направляется он в сторону, противоположную угловому ускорению.
Главный момент сил инерции относительно оси x
,
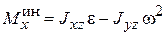где Jxz, Jyz – центробежные моменты инерции тела относительно соответствующих осей в точке О
Главный момент сил инерции точек тела относительно оси у
.
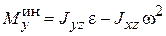Опять, если тело имеет плоскость симметрии, перпендикулярную оси вращения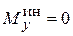 
.
Определив главные моменты сил инерции точек тела относительно взаимно перпендикулярных осей х, у, z, можно найти главный момент относительно точки О, начала координат,
,
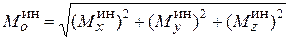1. Тело совершает плоскопараллельное движение.
Главный момент сил инерции точек тела при плоскопараллельном движении относительно центральной оси С, перпендикулярной плоскости движения, равен произведению момента инерции относительно этой оси на модуль углового ускорения
.
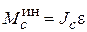Направляется этот момент в сторону, противоположную направлению углового ускорения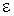 
.
Принцип Даламбера удобно использовать при решении задач, в которых требуется определить неизвестные силы и, иногда, ускорение.
Пример 1. Шар весом Р скатывается без скольжения по наклонной плоскости. Определим реакции плоскости и ускорение центра масс С.
Показываем внешние силы, действующие на шар: вес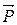 
, реакци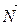и 
и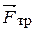 
(трение качения учитывать не будем). Добавляем силы инерции: главный вектор 
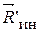, приложенный к центру масс, и главный момент сил инерции относительно центральной оси. Величина их
;
.
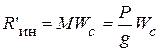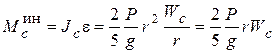Составляем уравнения равновесия:
; 
;
; 
;
; 
.
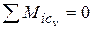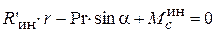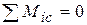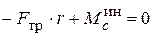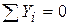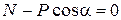Из первого уравнения находим ускорение центра масс.
Так как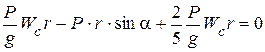 
, то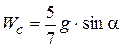 
.
Из второго уравнения – силу трения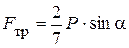 
;
из третьего – нормальную реакцию N = P cos α..
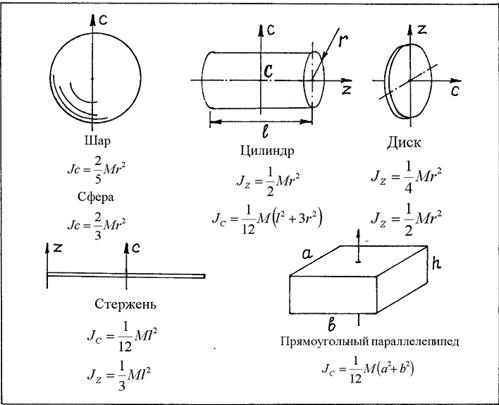
Моменты инерции некоторых тел, которые чаще всего встречаются при исследовании движения материальных систем:
