Самостоятельная работа обучающегося с преподавателем 1 страница
| № | Тема | Форма контроля и проведения |
| 1, 2 | Полная и средняя кривизна поверхности | 1.Конспект лекций 2. Решение домашних заданий 3. Решение задач СРС |
| 3-4 | Асимптотические линии. Геодезическая кривизна. Геодезические линии | 1.Конспект лекций 2. Решение домашних заданий 3. Решение задач СРС |
| 5-6 | Огибающая однопараметрического семейства кривых на плоскости | 1.Конспект лекций 2. Решение домашних заданий 3. Решение задач СРС |
| 7-8 | Огибающая однопараметрического семейства поверхностей | 1.Конспект лекций 2. Решение домашних заданий 3. Решение задач СРС |
| 9-10 | Некоторые приложения дифференциальной геометрии к механике | 1.Конспект лекций 2. Решение домашних заданий 3. Решение задач СРС |
Вопросы 1-ого рубежного контроля.
12. Вектор - функция скалярного аргумента.
13. Понятие линии. Параметризация кривой. Частные случаи кривых.
14. Гладкая кривая.
15. Параметрические уравнения и векторное уравнение кривой.
16. Касательная к кривой.
17. Длина дуги кривой
18. Естественная параметризация кривой.
19. Соприкасающаяся и нормальная плоскости кривой. Репер Френе.
20. Главная нормаль и бинормаль.
21. Кривизна и кручение кривой. Формулы Френе. Натуральные уравнения кривой.
22. Плоские кривые.
Вопросы 2-ого рубежного контроля.
13. Понятие поверхности. Параметризации поверхности. Частные случаи поверхности.
14. Гладкая поверхность.
15. Параметрические уравнения и векторное уравнение поверхности. Криволинейные ко- ординаты точки на поверхности.
16. Касательная плоскость и нормаль поверхности.
17. Первая квадратичная форма поверхности.
18. Длина дуги на поверхности
19. Угол между кривыми на поверхности.
20. Площадь поверхности.
21. Вторая квадратичная форма поверхности.
22. Нормальная кривизна поверхности. Индикатрисса Дюпена.
23. Главные направления в точке поверхности.
24. Главные кривизны.
Методические материалы по дисциплине
Основная литература
1. Атанасян Л.С. Геометрия. М., Просвещение. 1988,ч.1
2. Атанасян Л.С. Геометрия. М., Просвещение. 1988,ч.2
3. Александров П.С. Курс аналитической геометрии. М.Наука,
4. Сборник задач по геометрии (под редакции Л.С. Атанасян). М., Просвещение, 1980
5. Норден А.П. Краткий курс дифференциальной геометрии. М., Физматгиз, 2000
6. Александров А.Д. Нецветов Н.Ю. Геометрия. М., Наука , 1990
Дополнительная литература
4. А. В. Погорелов Дифференциальная геометрия. - М.: Наука, 1969
5. А.Л. Вернер, Б.Е. Кантор. Элементы топологии и дифференциальной геометрии. – М.: Просвещение, 1985.
6. Н. В. Ефимов. Высшая геометрия.- М., 1978
Буквенная система оценки учебных достижений
Обучающихся, соответствующая цифровому эквиваленту
По четырехбалльной системе
Таблица 1
| Оценка по буквенной системе | Цифровой эквивалент баллов | %-ное содержание | Оценка по традиционной системе |
| А | 4,0 | 95-100 | отлично |
| А- | 3,67 | 90-94 | |
| В+ | 3,33 | 85-89 | хорошо |
| В | 3,0 | 80-84 | |
| В- | 2,67 | 75-79 | |
| С+ | 2,33 | 70-74 | удовлетворительно |
| С | 2,0 | 65-69 | |
| С- | 1,67 | 60-64 | |
| D+ | 1,33 | 55-59 | |
| D | 1,0 | 50-54 | |
| Ғ | 0-49 | неудовлетворительно |
8.1. Учебные достижения обучающихся (знания, умения, навыки и компетенции) в соответствии с таблицей 1 оцениваются по 100 бальной шкале (Положительная оценка (А-, А «отлично», В-, В, В+ «хорошо», Д-, Д+, С-, С, С+ «удовлетворительно», оценка F «неудовлетворительно»).
График сдачи рубежного контроля
| Неделя | ||||||||||||||
| * | ** |
*- 1-ый рубежный контроль,**- 2- ый рубежный контроль
9.4. Письменные (устные) экзамены оцениваются также по 100-бальной (100%) шкале в соответствии с бально-рейтинговой буквенной системой (таблица 1).
Политика курса
Студент обязан выполнять следующие требования:
§ не опаздывать на занятия; не пропускать занятия;
§ активно участвовать в учебном процессе;
§ отрабатывать пропущенные занятия в определенное преподавателем время;
§ не разговаривать во время занятий, отключать сотовый телефон;
§ не жевать жвачку;
§ одеваться соответственно;
§ не списывать у других студентов на контрольных и экзаменах;
§ конструктивно поддерживать обратную связь на всех занятиях;
§ содействовать коллективной работе;
§ быть терпеливым, открытым, откровенным и доброжелательным к сокурсникам и преподавателям;
§ соблюдать правила внутреннего распорядка КГУ им. Коркыт Ата.
§ «УТВЕРЖДАЮ»
§ Зав. кафедрой физики и математики
§ __________Калиев Б.К.
§ «___» __________ 2015 г
§ Карта учебно-методической обеспеченности дисциплины (КУМОД)
§ «Геометрия»
§ (название дисциплины)
§ на 2015 - 2016 учебный год
| Специальность | Кол- во студентов | Учебники и учебные пособия | Кол-во | Конспекты лекций, методические указании к выполнению лабораторных и практических занятий, СРС и др. | Кол-во | |||
| Семестр | в библиот. | на кафедре | в библиот. | на кафедре | ||||
| 1-2 сем | Сем | |||||||
| Математика | Атанасян С.Л. Геометрия 1, М,. «Мысль и жизнь», 2001 г. - 376 с | Базылев В. Т. Сборник задач по геометрии / В. Т. Базылев, К. И. | ||||||
| Атанасян Л. С. Геометрия в двух частях. Часть 2. / Л. С. Атанасян, В. Т. Базылев. –– изд. 2-е стереотипное – М.: КноРус, 2011. – 424 с. | Атанасян С. Л. Сборник задач по геометрии. Часть 1. / С. Л. Атанасян, В. И. Глизбург. – М.: ЭКСМО, 2007. – 336 с. | |||||||
| Ильин В.А., Позняк Э.Г. Аналитическая геометрия: учебник для ВУЗов. 7-е изд., стер. − М.: Физматлит, 2006. − Гл. 5, §§ 4,5, с. 135-143 | Атанасян С. Л. Сборник задач по геометрии. Часть II. / С. Л. Атанасян, Н. В. Шевелева, В. Г. Покровский. – М.: ЭКСМО, 2008. – 320 с. |
Преподаватель__________________________________
| Лекционный комплекс | ||||||
| 1.1. Пространственная кривая. Вектор-функция скалярного аргумента | ||||||
Известно, что кривая может быть задана своими параметрическими уравнениями. При этом каждая координата текущего радиус-вектора кривой (или текущей точки кривой) является функцией некоторого параметра 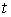 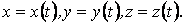 (1.1) Соответственно текущий радиус-вектор имеет вид (1.1) Соответственно текущий радиус-вектор имеет вид 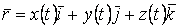 , (1.2) Где , (1.2) Где 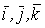 – единичные векторы прямоугольной декартовой системы координат. Вектор – единичные векторы прямоугольной декартовой системы координат. Вектор 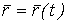 является одновременно и вектором, и функцией; его называют Вектор-функцией скалярного аргумента. Для дальнейшего предполагаем, что функции является одновременно и вектором, и функцией; его называют Вектор-функцией скалярного аргумента. Для дальнейшего предполагаем, что функции 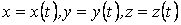 имеют непрерывные производные достаточно высокого порядка. Поскольку имеют непрерывные производные достаточно высокого порядка. Поскольку 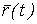 Является функцией, для него можно ввести понятие предела Является функцией, для него можно ввести понятие предела 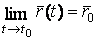 , Где , Где 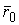 – некоторый постоянный вектор, и понятие производной – некоторый постоянный вектор, и понятие производной 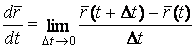 . Очевидно, что . Очевидно, что 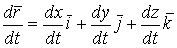 . (1.3) . (1.3)
| |||||
Рассмотрим векторное уравнение кривой (1.2). Выделим две точки на кривой М и 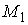 (рис.1.1), которые соответствуют значениям параметра T и (рис.1.1), которые соответствуют значениям параметра T и 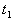 . Хорда, соединяющая точки М и . Хорда, соединяющая точки М и 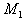 , определяет вектор , определяет вектор 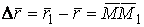 . При переходе к пределу, когда . При переходе к пределу, когда 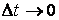 , точка , точка 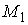 , двигаясь по дуге , двигаясь по дуге 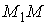 , в пределе совпадает с точкой М. При этом , в пределе совпадает с точкой М. При этом 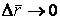 при при 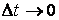 , но отношение , но отношение 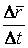 может сохранить в пределе конечное значение. Секущая в пределе займет положение касательной к линии в может сохранить в пределе конечное значение. Секущая в пределе займет положение касательной к линии в 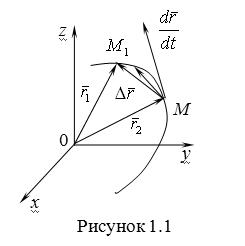 точке М. На этой касательной и будет лежать вектор производной точке М. На этой касательной и будет лежать вектор производной 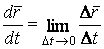 . Последний результат можно сформулировать в виде теоремы. Теорема. Производная от радиус-вектора текущей точки кривой имеет направление касательной к кривой. Поскольку предел отношения длины дуги . Последний результат можно сформулировать в виде теоремы. Теорема. Производная от радиус-вектора текущей точки кривой имеет направление касательной к кривой. Поскольку предел отношения длины дуги 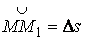 к длине хорды к длине хорды 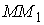 равен 1, т. е. равен 1, т. е. 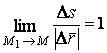 , то , то 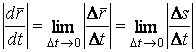 . . |
Степень искривленности кривой определяется углом поворота касательной к кривой (углом смежности). Однако этот угол зависит от длины дуги кривой AB (рис.1.2). Введем среднюю кривизну кривой для заданной дуги AB
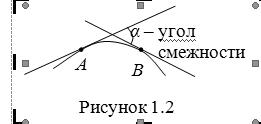
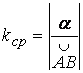 .
.
Обозначив
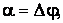

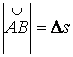 ,
,
запишем 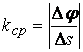 .
.
Так как 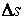 – конечная величина, значение средней кривизны зависит от выбора
– конечная величина, значение средней кривизны зависит от выбора 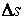 . Для характеристики степени искривленности (кривизны) кривой в точке необходимо перейти к пределу при
. Для характеристики степени искривленности (кривизны) кривой в точке необходимо перейти к пределу при 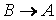 .
.
Определение. Кривизна кривой в точке А равна
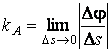 . (1.5)
. (1.5)
Для получения формулы вычисления кривизны кривой, заданной уравнением 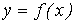 в прямоугольных декартовых координатах, используем рис. 1.3.
в прямоугольных декартовых координатах, используем рис. 1.3.
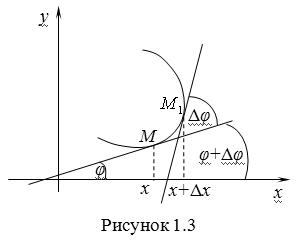 Исходя из формулы (1.5), запишем
Исходя из формулы (1.5), запишем
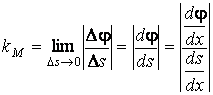 .
.
Вспоминая геометрический смысл производной, 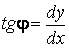 , получаем
, получаем
 ,
,
Тогда 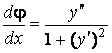 (здесь и далее
(здесь и далее 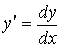 и т. д.), кроме того,
и т. д.), кроме того, 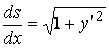 . Окончательно
. Окончательно
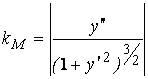 . (1.6)
. (1.6)
Пример 1. Парабола 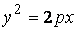 . Тогда
. Тогда 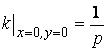 .
.
Пример 2. Прямая 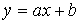 , здесь
, здесь  и
и 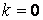 в любой точке.
в любой точке.
Пример 3. Окружность радиуса R. Здесь удобнее использовать не формулу (1.5), а выражение для средней кривизны.
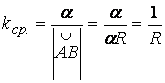 .
.
Переход к пределу не изменит этого значения, и, следовательно, кривизна в любой точке окружности равна 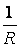 .
.
Во многих задачах и теоретических выкладках помимо кривизны вводят Радиус кривизны
 . (1.7)
. (1.7)
| 1.5. Кривизна пространственной кривой и её вычисление |  |  |  |
Определение кривизны по формуле (1.5) имеет место и в пространственном случае. В качестве основного “естественного параметра” принимаем длину дуги кривой 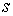 , так что текущий радиус-вектор кривой запишем как , так что текущий радиус-вектор кривой запишем как 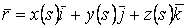 . Рассмотрим модуль вектора . Рассмотрим модуль вектора 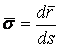 , а именно , а именно 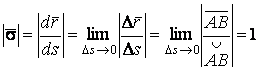 , Т. е. , Т. е. 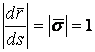 в любой точке кривой. Пусть вектор в любой точке кривой. Пусть вектор 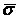 направлен по касательной к кривой в некоторой точке А (рис.1.4). Задавая приращение параметра направлен по касательной к кривой в некоторой точке А (рис.1.4). Задавая приращение параметра 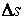 , переходим к точке В, а вектор , переходим к точке В, а вектор 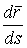 , направленный по касательной к кривой в точке В, обозначим через , направленный по касательной к кривой в точке В, обозначим через 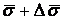 . Так как . Так как 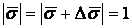 , о , о 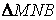 является равнобедренным, поэтому, обозначив угол поворота касательной через является равнобедренным, поэтому, обозначив угол поворота касательной через 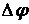 , запишем , запишем 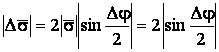 . . 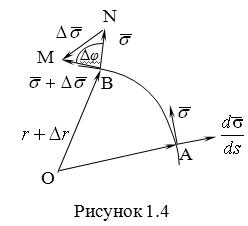 Отсюда получаем Отсюда получаем 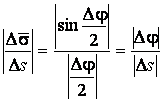 И, следовательно, в пределе при И, следовательно, в пределе при 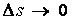 находим, что находим, что  , Как следует из определения кривизны. С другой стороны, , Как следует из определения кривизны. С другой стороны,  . Итак, мы получаем следующую формулу для вычисления кривизны . Итак, мы получаем следующую формулу для вычисления кривизны  (1.8) Далее, поскольку (1.8) Далее, поскольку 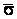 – единичный вектор, то из формулы (1.4) следует, что вектор – единичный вектор, то из формулы (1.4) следует, что вектор 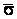 ортогонален вектору ортогонален вектору 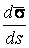 и, следовательно, этот последний вектор лежит в нормальной плоскости к кривой в данной её точке. Соответствующее направление называют направлением главной нормали. Обозначив единичный вектор главной нормали через и, следовательно, этот последний вектор лежит в нормальной плоскости к кривой в данной её точке. Соответствующее направление называют направлением главной нормали. Обозначив единичный вектор главной нормали через 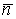 , запишем так называемую Первую формулу Френе , запишем так называемую Первую формулу Френе 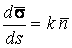 , (1.9) Где коэффициент пропорциональности и является кривизной, поскольку , (1.9) Где коэффициент пропорциональности и является кривизной, поскольку  , т. е. , т. е. 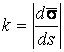 . (Направление главной нормали . (Направление главной нормали 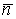 выбирается таким образом, чтобы величина выбирается таким образом, чтобы величина 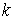 была положительной). Перейдем теперь к вычислению кривизны в более общем случае, когда радиус-вектор кривой есть функция произвольного параметра была положительной). Перейдем теперь к вычислению кривизны в более общем случае, когда радиус-вектор кривой есть функция произвольного параметра 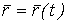 . Справедливо равенство . Справедливо равенство 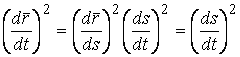 , (1.10) Поскольку ранее было установлено, что , (1.10) Поскольку ранее было установлено, что 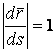 . Дифференцируя равенство (1.10) по параметру T, имеем . Дифференцируя равенство (1.10) по параметру T, имеем 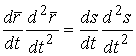 . (1.11) Вновь возводя в квадрат, получим . (1.11) Вновь возводя в квадрат, получим  (1.12) Теперь вычисляем (1.12) Теперь вычисляем  И И  . Отсюда . Отсюда  . В последнюю формулу, исключая естественный параметр . В последнюю формулу, исключая естественный параметр 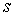 , подставим вместо , подставим вместо  , ,  и и  соответствующие выражения из вспомогательных формул (1.10), (1.11), (1.12). Получаем соответствующие выражения из вспомогательных формул (1.10), (1.11), (1.12). Получаем   , (1.13) Где знак ‘‘´’’ означает векторное произведение. В том, что , (1.13) Где знак ‘‘´’’ означает векторное произведение. В том, что 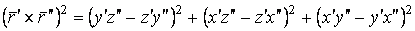 и и 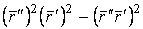 совпадают, можно легко убедиться непосредственным вычислением (здесь для краткости введён символ (¢) как знак дифференцирования по параметру T). В случае если совпадают, можно легко убедиться непосредственным вычислением (здесь для краткости введён символ (¢) как знак дифференцирования по параметру T). В случае если 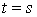 , из (1.13) получаем , из (1.13) получаем 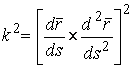 . (1.14) Если рассматриваемая кривая представляет собой траекторию движения некоторой материальной точки, а . (1.14) Если рассматриваемая кривая представляет собой траекторию движения некоторой материальной точки, а 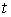 – время, то, вводя векторы скорости – время, то, вводя векторы скорости 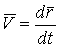 и ускорения и ускорения 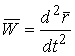 , можно переписать формулу (1.13) в виде , можно переписать формулу (1.13) в виде 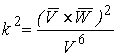 Пример. Винтовая линия, которая задана уравнениями Пример. Винтовая линия, которая задана уравнениями 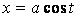 , , 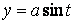 , , 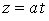 , где , где 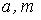 – некоторые постоянные. Выпишем векторы – некоторые постоянные. Выпишем векторы 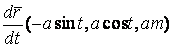 и и 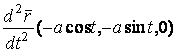 . Тогда . Тогда 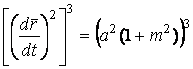 ; ;  И, следовательно, И, следовательно, 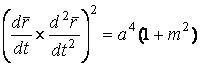 . Итак, по формуле (1.13) . Итак, по формуле (1.13) 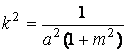 , Т. е. кривизна винтовой линии одна и та же во всех точках данной кривой. , Т. е. кривизна винтовой линии одна и та же во всех точках данной кривой. | |||
| 2.1. Формулы Френе. Трёхгранник Френе |  |  |  |

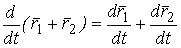 . Действительно, приращение суммы функций складывается из приращений слагаемых
. Действительно, приращение суммы функций складывается из приращений слагаемых 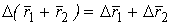 , отсюда
, отсюда 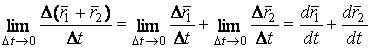 . 2.
. 2. 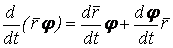 , Где
, Где 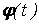 – дифференцируемая скалярная функция. Действительно,
– дифференцируемая скалярная функция. Действительно, 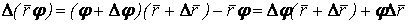 , Откуда
, Откуда 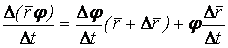 , И после перехода к пределу при
, И после перехода к пределу при 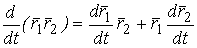 , Где всюду рассматриваются скалярные произведения векторов. Действительно,
, Где всюду рассматриваются скалярные произведения векторов. Действительно, 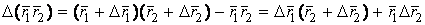 , Откуда получаем искомое, разделив на
, Откуда получаем искомое, разделив на 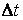 и переходя к пределу при
и переходя к пределу при 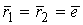 , где
, где 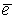 – единичный вектор. Тогда
– единичный вектор. Тогда 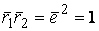 , и из формулы дифференцирования скалярного произведения имеем
, и из формулы дифференцирования скалярного произведения имеем 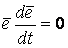 (1.4) Формула (1.4) означает, что Производная единичного вектора ортогональна этому вектору. Этот результат и будет часто использоваться в дальнейшем. 4.
(1.4) Формула (1.4) означает, что Производная единичного вектора ортогональна этому вектору. Этот результат и будет часто использоваться в дальнейшем. 4. 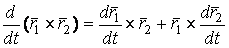 , Где знак “
, Где знак “ 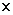 ” является символом векторного произведения. Действительно,
” является символом векторного произведения. Действительно, 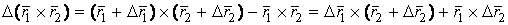 . Разделив на
. Разделив на 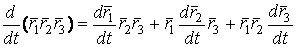 . Доказательство опускаем. Его можно получить без большого труда, комбинируя некоторые предыдущие формулы. 6. Дифференцирование сложной функции. Пусть
. Доказательство опускаем. Его можно получить без большого труда, комбинируя некоторые предыдущие формулы. 6. Дифференцирование сложной функции. Пусть 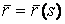 ,
, 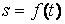 , тогда
, тогда 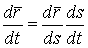 . Действительно,
. Действительно, 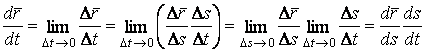 . 7. Для вектор-функции не имеет место теорема Ролля, а значит и теорема Лагранжа. Однако ряд Тейлора с остаточным членом может быть выписан и для вектор-функции. 1.3 Касательная к линии
. 7. Для вектор-функции не имеет место теорема Ролля, а значит и теорема Лагранжа. Однако ряд Тейлора с остаточным членом может быть выписан и для вектор-функции. 1.3 Касательная к линии