Метод разделения для уравнений

ЭЛЛИПТИЧЕСКОГО ТИПА

Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма Лиувилля своеобразны, их граничные ус- ловия определяются спецификой областей:

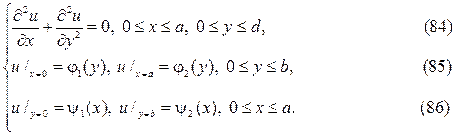
следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач

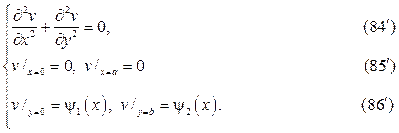
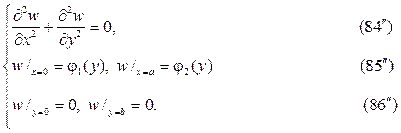
Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.

Рассмотрим задачу Дирихле для круга

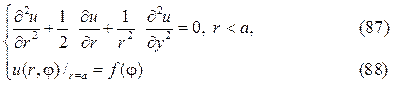
где f(j)кусочно-непрерывная функция.

Следуя схеме метода Фурье полагаем

u (r, j) = R (r) F(j) (89)

подставляем в (87) и разделяем переменные. В результате получим ра -венство

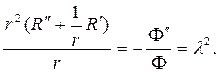(90)

Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма Лиувилля

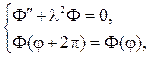
откуда следует, что

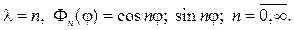(91)

Возвращаясь к (80), решаем уравнение для радианальной функции. При

n ³ 1 имеем

r²R² + rR¢ n²R = 0,

решение следует искать в виде степенной функции R=r^m. Для определе- ния m получим соотношение

m(m 1)r^m+m r^m 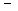n²r^m=0Û m² 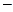n²=0,

поэтому

m = ± n, R_n(r) = rⁿ; r^-n. (92)

Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции

R₀(r) = 1; lnr.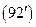

С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге

1, r cosj, r sin j, …, rⁿ cosnj, rⁿsin nj, … .

Если предположить, что ряд

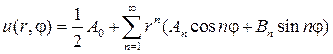(93)

можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем

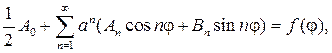(94)

откуда с учетом формул коэффициентов Фурье следует

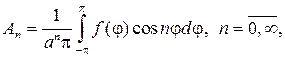(95)

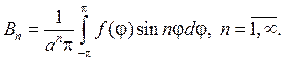(96) Итог состоит в том, что решение задачи (87 88) дается рядом (93), коэффициенты которого определены равенствами (95-96).

Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r<a. При его нахождении мы не привлекали радиальных функций r^-n и lnr, поскольку они разрывны в

центре круга r=0.

Напротив, если рассматривать область r>a, то нельзя привлекать r^-n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом

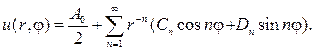(97)

В случае кругового кольца a<r<b необходимо привлекать все встре- тившиеся выше радиальные функции (92 92¢) и гармоническая функция примет вид

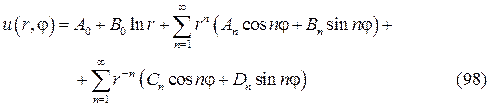
Отметим, что соотношения (93), (97 98) позволяют решать также вторую и третью краевые задачи для названных областей.

Замечание 2. В простейших случаях, когда f(j) есть тригонометричес-

кий полином, т.е. линейная комбинация

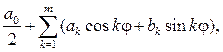
коэффициенты A_n и B_n находятся из равенства (94) путем приравнивания коэффициентов возле одноименных функций слева и справа. Решение задачи (87 88) будет на этот раз представлено в виде конечной суммы.

Рассмотрим теперь первую краевую задачу для уравнения Лапласа в шаре радиуса а:

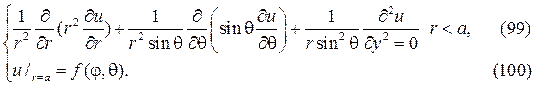
Полагая u(r,j,q) = R(r)Y(j,q), после подстановки в (99) и разделения переменных получим равенство

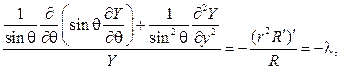(101)

которое распадается на два дифференциальных уравнения с неизвестным параметром l.Их нужно решать при условии ограниченности в области изменения переменных 0 £ r £ a, 0 £ q £ p,0 £ j £ 2p, и периодичность по переменной j с периодом 2p так, что Y(j+2p,q)=Y(j,q).

Дифференциальное уравнение

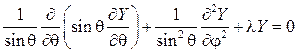(102 )

снова решаем разделением переменных, полагая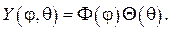

Подставляем в (102) и находим

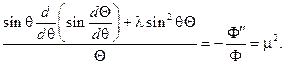(103)

Для функции F(j) с учетом периодичности получим уже встретившуюся выше при решении задачи Дирихи для круга задачу Штурма Лиувилля

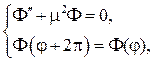
откуда согласно формуле (91)

m=m, F_m(j)=cosmj; sinmj; m= .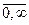

Тогда второе из уравнений (73) примет вид

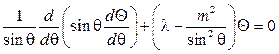(104)

и его нужно решать при условиях ограниченности

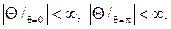(105)

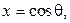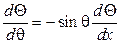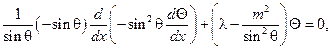В уравнении (104) изменим независимую переменную, полагая тогда и или с

учетом того, что sin²q= 1-x², найдем

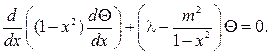(104¢)

Соответственно и граничные условия (105) перейдут после замены в неравенства

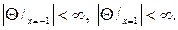(105′)

Задача (104¢) (105¢) есть известная задача для присоединенных функций Лежандра, ее решение (см., например, [3], стр. 115)

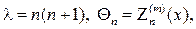
и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):

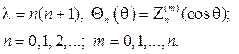(106)

Составив произведения функций (106) на найденные выше функции F_m(j), получим множество решений уравнения (102)

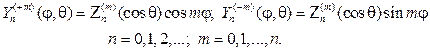(107)

Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.

Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m₁¹m₂ или n₁¹n₂

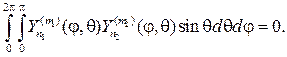(108)

Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции

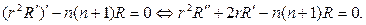
Оно имеет решение в виде степенной функции R=r^m. Действительно, после подстановки

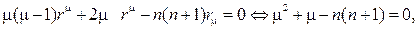
откуда находим значения m=n; (n+1) и соответственно решения

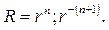(109)

Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:

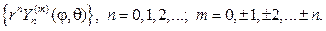
Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами

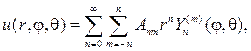(110)

который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.

Для нахождения коэффициентов А_nm подставим (110) в (100), тогда

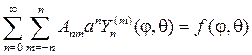
и с учетом (108) найдем

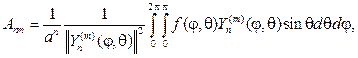(111)

где

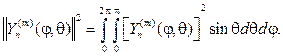
Последний интеграл вычисляется и при m=0 :

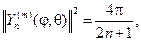(112)

если же |m| ³ 1, то имеем

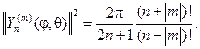(113)

Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).

Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам

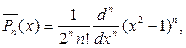(114)

соответственно

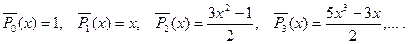
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.

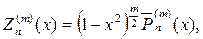(115)

в частности будем иметь

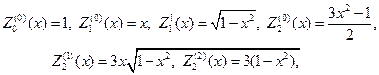
и при любом n

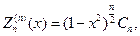(116)

где С_n определенная константа.

С учетом (107), (115) и (116) выпишем несколько сферических функций:

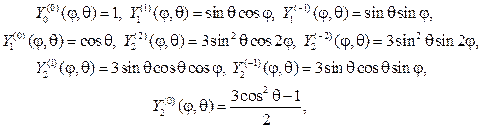
и при любом n

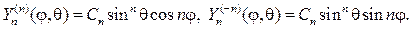(117)

Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд

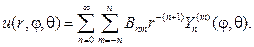(118)

Общий вид гармонической функции в шаровом слое a < r < b получа- ется сложением формул (110) и (118).

Замечание5. При некоторых правых частях удается найти частное ре- шение уравнения Пуассона и свести краевую задачу для уравнения Пуас- сона к краевой задаче для уравнения Лапласа, которая решается методом Фурье.

248. Найдите решение краевой задачи в прямоугольнике

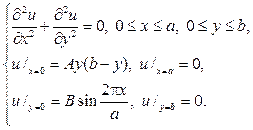
Р е ше н и е. Как и в общем случае, полагая u=v(x,y)+w(x,y), где v(x,y) есть решение задачи

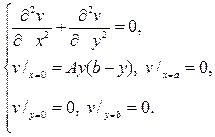
Для ее решения берем v(x,y)=X(x)Y(y), тогда

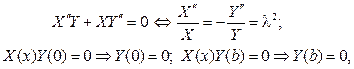
и мы пришли к задаче Штурма Лиувилля

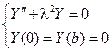
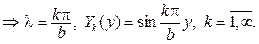
Для функции X(x) будем иметь уравнение 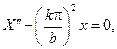общее ре-

шение которого может быть записано в виде

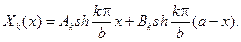
Тогда сумма ряда (если его можно дважды дифференцировать почленно)

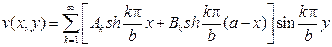
будет гармонической функцией в прямоугольнике. В силу первого из граничных условий будем иметь

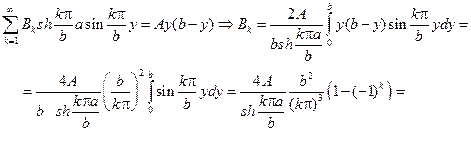
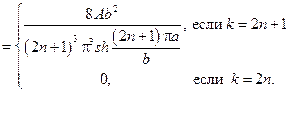
Из второго граничного условия найдем

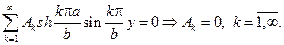
Подставляя значения найденных коэффициентов в ряд, придем к ра -венству

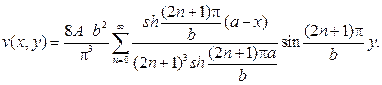
Функция w(x,y) есть решение задачи Дирихле

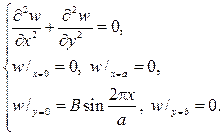
Снова по методу Фурье w(x,y) = X(x)Y(y). На этот раз придем к задаче

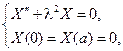
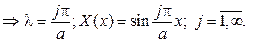
Для функции Y(y)получится дифференциальное уравнение

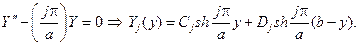
Перемножая Y_j(y) и X_j(x) и суммируя по всем j, найдем гармоничес- кую в прямоугольнике и равную нулю на сторонах х=0 и х=а функцию

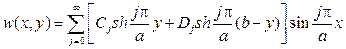
С учетом граничного условия при y=0 имеем

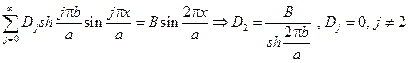
Из граничного условия w_/y=b=0 вытекает

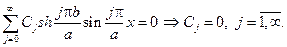
Таким образом получаем, что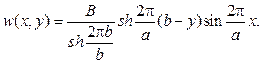

Складывая найденные функции v(x,y) и w(x,y), придем к ответу

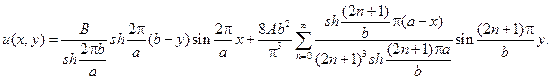
249. Найдите решение краевой задачи в прямоугольнике

W={(x,y): 0 £ x £ a, 0 £ y £ b}

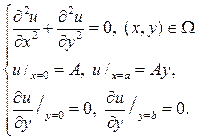
По методу Фурье полагаем u(x,y) = X(x)Y(y) и приходим к равенству

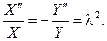
Из граничных условий при y=0и y=b найдем 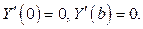Далее из задачи Штурма Лиувилля

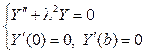
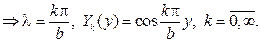
Для функции Х(х) имеем дифференциальное уравнение

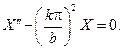
Если 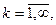то его общее решение имеет вид

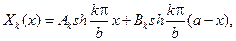
при k=0 общее решение будет линейной функцией Х₀(х)=А₀х+В₀. Гармо- ническая функция в W

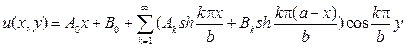
будет, очевидно, удовлетворять условиям 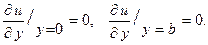Остается выбрать ее коэффициенты так, чтобы выполнялись граничные условия на сторонах x=0 и x=a.

Будем иметь

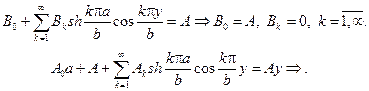
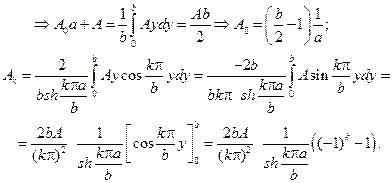
При четных k=2n коэффициенты A_2n=0,поэтому окончательно реше-ние запишется в виде

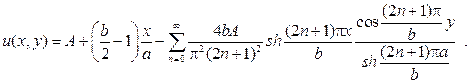
250. Найдите стационарное распределение температуры в прямоугольной пластине 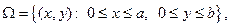если стороны х=а и у=b покрыты тепловой изоляцией, стороны х=0 и у=0 поддерживаются при нулевой температуре, и в пластинке выделяется тепло с плотностью Q.

Р е ш е н и е. Текстовая задача равносильна следующей краевой зада- че (k – коэффициент внутренней теплопроводности)

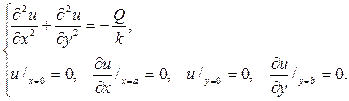
Возьмем частное решение, зависящее только от у

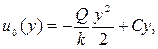
выберем константу С так, чтобы

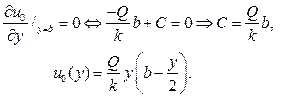
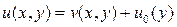Полагая теперь , придем к краевой задаче для уравнения Лапласа относительного новой неизвестной функции v(x,y) :

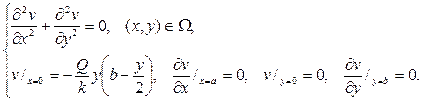
Как обычно, полагаем теперь 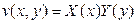и приходим к диффе- ренциальным уравнениям

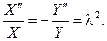
Из граничных условий 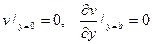находим, что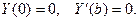

Следовательно, нужно решать задачу Штурма Лиувилля:

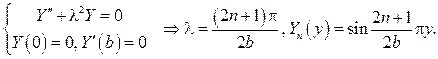
Для функции Х(х) будем иметь уравнение 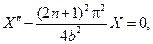и его решение может быть записано в виде

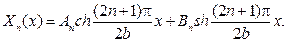
Гармоническая в W функция

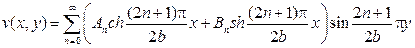
удовлетворяет условиям 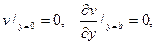и остается выбрать коэффи- циенты A_n и B_n так, чтобы выполнялись два других граничных условия

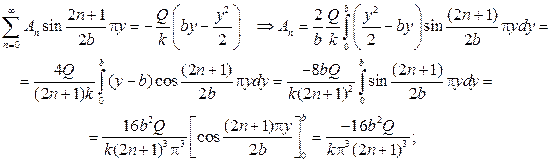
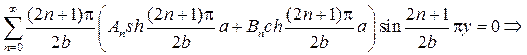
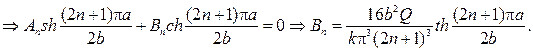
Подставляя найденные коэффициенты в ряд, найдем

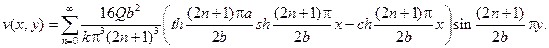
Решение исходной задачи получится окончательно в форме

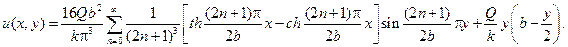
251. Найдите стационарную температуру u(r,z) внутренних точек ци- линдра 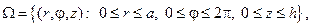если температура нижнего основания и боковой поверхности равна нулю, а температура верхнего основания u(r,h)=f(r).

Р е ш е н и е. Здесь нужно решать уравнение Лапласа в W , и поскольку температура не зависит от j , то 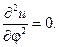Стало быть краевая задача запи- шется в форме

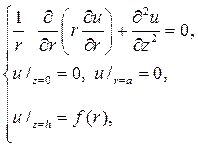
и решать ее нужно методом Фурье, полагая u(r,z)=R(r)Z(z). После разде- ления переменных в дифференциальном уравнении получим

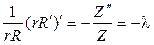
Из граничного условия на боковой поверхности u/_r=a=0 следует, что R(a)=0, поэтому с учетом обращения в нуль коэффициента k(r)=r при r=0 придем к задаче Штурма Лиувилля:

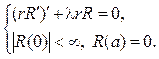
Собственные функции этой задачи образуют ортогональную систему с весом r на отрезке [0,а] (см. теорему 2 из параграфа 3). Дифференциальное уравнение

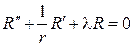
после введения новой переменной 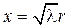приводится к уравнению Бес- селя нулевого порядка:

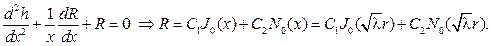
Применяя граничные условия, будем иметь с учетом того, что J₀(0)=1, N₀(0)=¥ и 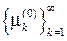положительные нули функции J₀(x) :

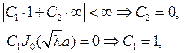
следовательно

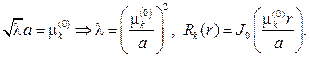
Из дифференциального уравнения

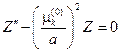
вытекает, что

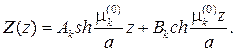
Составляем ряд

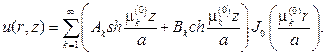
Из условия u/_z=0=0 найдем, что

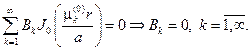
Из граничного условия на верхнем основании (см. (81))

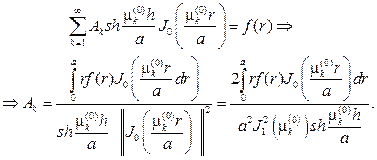
С учетом найденных значений коэффициентов придем к ответу:

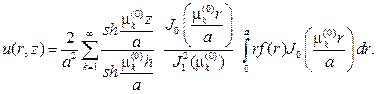
252. Найдите стационарную температуру u(r,z) внутренних точек цилин- дра 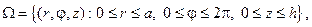если температура верхнего

основания и боковой поверхности равна нулю, а к нижнему основанию подводится постоянный тепловой поток q.

Р е ш е н и е. Текстовая задача равносильна следующей краевой зада-

че (k– коэффициент теплопроводности) в W

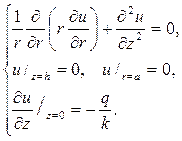
Как и в предыдущей задаче находится гармоническая в W функция, равная нулю на боковой поверхности

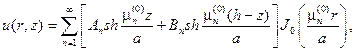
здесь вместо линейной комбинации гиперболических синуса и косинуса взята линейная комбинация гиперболического синуса и его сдвига. При- меняя условие u/_z=h=0,

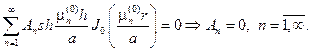
Из граничного условия на нижнем основании будем иметь

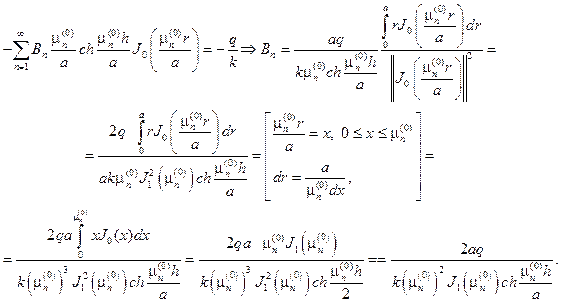
С учетом значений коэффициентов А_n и B_n придем к ответу

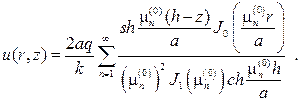
253. Найдите решение краевой задачи

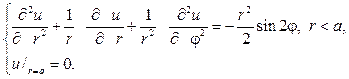
Р е ш е н и е. Сперва найдем частное решение уравнения Пуассона в виде u₀(r,j)=v(r)sin2j.

Тогда

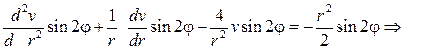
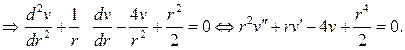
Очевидно, решение уравнения Эйлера нужно искать в виде v=cr⁴, и получим

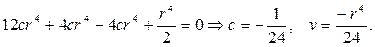
Таким образом, частным решением будет функция

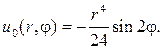
Вводим новую неизвестную функцию w(r,j) , полагая

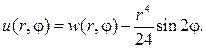
Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа

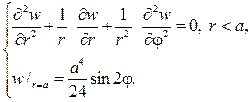
Согласно (93), решение этой задачи дается формулой

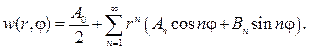
Подставляя ее в граничное условие, получим

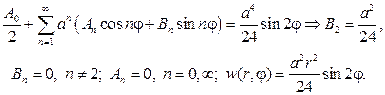
Ответом в задаче будет функция

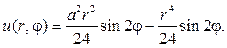
254. Найдите решение первой краевой задачи для уравнения Гельмгольца

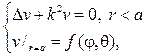
предполагая, что k не является собственным значением задачи

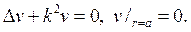
Р е ш е н и е. Запишем уравнение в сферических координатах

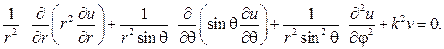
Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:

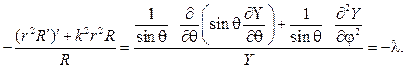
Функция 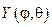будет решением уравнения (72), которое нужно решать при условии ограниченности и 2p-периодичности по j. В результате при- дем к сферическим функциям при l=n(n+1):

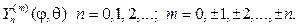
Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение

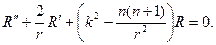
Выполняя в этом уравнении замену

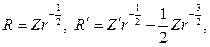
придем к соотношению относительно новой функции Z(r):

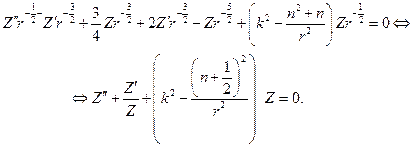
Последнее уравнение в качестве ограниченных в окрестности нуля

r=0 решений имеет бесселевы функции

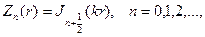
соответственно будем иметь набор радиальных функций

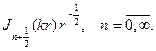
Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:

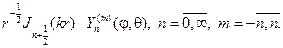
Составляем ряд с числовыми коэффициентами

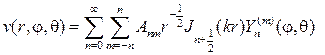(119)

и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a

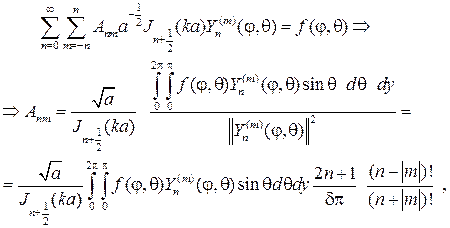
где d = 4 при m = 0 и d =2 при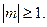

При найденных коэффициентах A_nm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.

255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1 < r < 2, чтобы выполнялись условия

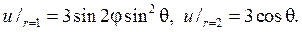
Р е ш е н и е. Согласно (80), (88) и замечанию 4 общий вид гармонической функции в шаровом слое

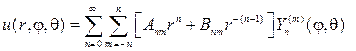(120)

Поскольку 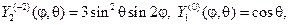то можно считать в (120) все коэффициенты равными нулю, кроме 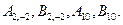Отмечен- ные четыре коэффициента будут решениями уравнений

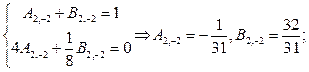
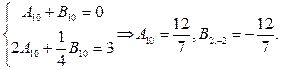
В итоге получим, что искомая гармоническая функция в шаровом слое имеет вид

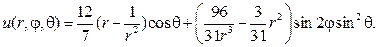
256. Найдите решение краевой задачи в прямоугольнике

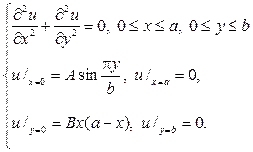
257. Найдите стационарное распределение температуры внутри тонкой прямоугольной пластинки 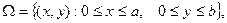если к стороне у=0 подводится постоянный тепловой поток q, а остальные три стороны поддерживаются при постоянной температуре u₁.

258. Найдите потенциал электростатического поля u(x,y) внутри прямоу- гольника 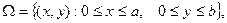если вдоль стороны у=0потенци- ал равен u₁, а три другие стороны заземлены. Электрические заряды внут- ри W отсутствуют.

259. Найдите стационарное распределение температуры u(x,y) в прямоу- гольной пластинке 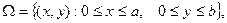если стороны х=а и у=b покрыты тепловой изоляцией, две другие стороны поддерживаются при нулевой температуре, а в пластинке выделяется тепло с постоянной плот- ностью q.

260. Найдите решение уравнения Лапласа в полуполосе 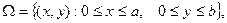удовлетворяющее краевым условиям u(0,y)=0, u(a,y)=0,u(x,0)=A(a x), u(x,¥)=0.

261. Найдите решение уравнения Лапласа в полуполосе 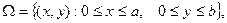удовлетворяющее краевым условиям u(0,y)=0,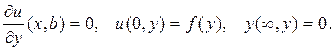

262. Найдите распределение потенциала электростатического поля u(x,y,z) внутри прямоугольного параллелепипеда {0£x£a, 0£y£b, 0£z£c}, если его боковые грани и верхнее основание заземлены, а нижнее основание заряжено до потенциала u₁.

263.Найдите стационарную температуру u(r,z) внутренних точек цилинд- ра радиуса а и высотой h, если температура обоих оснований равна нулю и на боковой поверхности u(r,z)/_r=a=f(z).

264. Найдите стационарное распределение температуры в цилиндре {0£r£a, 0£j£2p, 0£z£h}, если нижнее основание имеет температуру u₁, а на остальной поверхности температура равна нулю.

265. Нижнее основание цилиндра {0£r£a, 0£j£2p, 0£z£h}, имеет нуле- вую температуру, верхнее теплоизолировано, а температура боковой по- верхности равна 0. Найдите стационарное распределение температуры внутри цилиндра.

Решите следующие краевые задачи

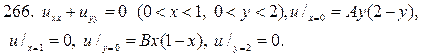
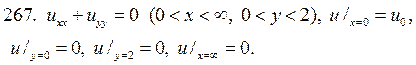
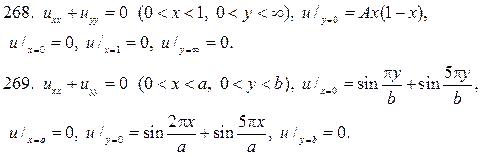
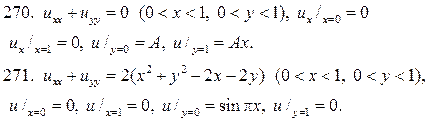
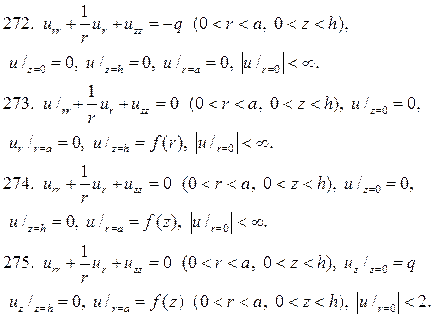
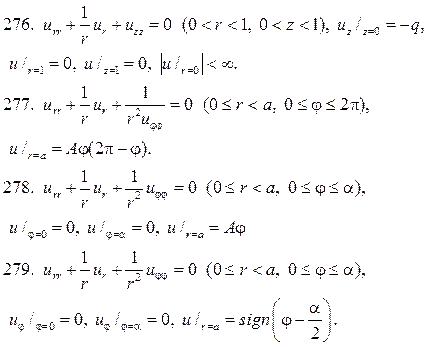
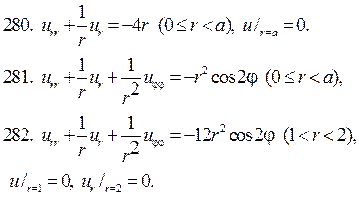
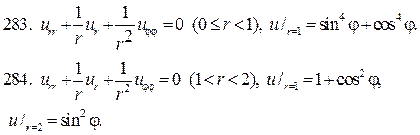
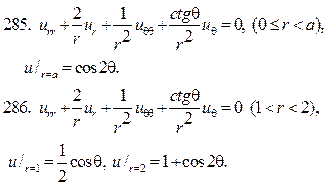
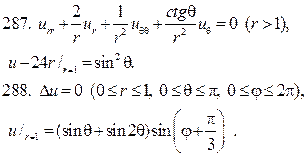
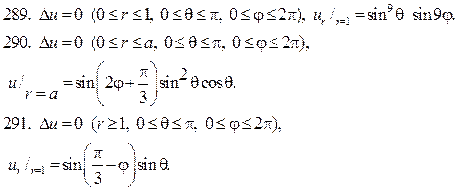
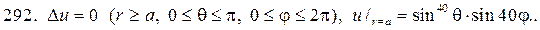
Литература

1. Смирнов В.И. Курс высшей математики. Т. 1 5. М.: Физматгиз, 1958-1960.

2. Ильин В.А., Позняк Э. Г. Основы математического анализа. М.: Наука, 1965.

3. Будак Б.М., Фомин С.В. Кратные интегралы и ряды. М.: Наука, 1965.

4. Свешников А. Г., Тихонов А. Н.Теория функций комплексной переменной. М.: Наука, 1967.

5. Демидович Б. П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1972.

6. Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.

7. Арсенин В. Я. Математическая физика.- М.: Наука, 1966.

8. Владимиров В. С. Уравнения математической физики. М.: Наука, 1967.

9. Кошляков Н. С., Глинер Э. Б., Смирнов М. М. Основные дифференциальные уравнения математической физики. М.: Физматгиз, 1962.

10. Петровский И. Г. Лекции об уравнениях с частными производны- ми. М.: Физматгиз, 1961.

11. Тихонов А. Н., Самарский А. А. Уравнения математической физии- ки. М.: Наука, 1966.

12. Будак Б. М., Самарский А. А., Тихонов А. Н . Сборник задач по математической физике. М.:Гостехиздат, 1956.

13. Смирнов М. М. Задачи по уравнениям математической физики. М.: Наука, 1968.

14. Сборник задач по уравнениям математической физике./ Под редакцией В.С.Владимирова. М.: Наука, 1974.

15. Бицадзе А. В., Колиниченко Д. Ф. Сборник задач по уравнениям математической физике. М.: Наука, 1977.

16. Русак В.Н. Математическая физика. Мн.: Дизайн ПРО, 1998.

Содержание

Предисловие..………………………………………………………………....3

§1.Ряды и преобразования Фурье…….……………………………………...4

§2.Операционное исчисление………………………………………………11

§3. Классификация и приведение к каноническому виду уравнений в

частных производных второго порядка……………………………….…..21

§4. Простейший вариант метода разделения переменных………………..27

§5. решение смешанной задачи с неоднородностями в уравнении или в граничных условиях……………………………………………………...…39

§6. Метод разделения переменных для параболических уравнений……49

§7. Цилиндрические функции и решение смешанных задач для уравнений

гиперболического и параболического типов………………………………60

§8. Метод разделения для уравнений эллиптического типа…………..…81

Литература………………………………………………………………….103

Учебное издание

Задачи по математической

и их решения

Авторы=составители:

Русак Валентин Николаевич,

Филиппова Нелли Константиновна.

В авторской редакции

Технический редактор Т. К. Раманович

Корректор О. Н. Кохно

Копьютерная верстка

Ответственный за выпуск Л. В. Рутковская

Подписано в печать 00.00.2006. Формат Бумага офсетная.

Гарнитура Таймс. Печать офсетная. Усл. печ. л. Уч. изд. Л. 4,0.

Тираж экз. Зак.

Белорусский государственный университет.

Лицензия на осуществление издательской деятельности

№02330/0056804 от 02.03.2004.

220050, Минск, проспект Независимости, 4.

Отпечатано с оригинала=макета заказчика.

Республиканское унитарное предприятие

«Издательский центр Белорусского государственного университета».

Лицензия на осуществление полиграфической деятельности

№02330/0056850 от 30.04.2004.

220050, Минск, ул. Красноармейская, 6.