Возможное оформление по типам задач.

Общие требования к оформлению задач

1.В задачах обязательно должна быть краткая запись условия задачи в наиболее подходящей к данному типу задачи наглядной форме (текстовой, табличной, графической или схематичной) и поставлен главный вопрос задачи!

2.Ecли решение задачи содержит несколько действий, то после каждого действия должна быть приведена в скобках единица измерения результата действия, а после единицы измерения пояснение к действию в сжатой форме!

(В самих выражениях (числовых или буквенных) единицы измерения не должны содержаться. Необходимые переводы из одних единиц измерения в другие делаются либо сразу в краткой записи, либо перед конкретным действием.)

3.Действия, содержащие вычисления с многозначными числами, должны обязательно сопровождаться расчетами в столбик.(Калькулятор допустим только лишь для проверки расчетов при выполнении домашнего задания.)

4.В конце обязательно должен быть ответ к задаче!

5.В геометрических задачах связанных с нахождением длин отрезков, величин углов, площадей фигур и др. геометрических величин, за исключением редких (!) случаев, должен быть чертеж с соответствующими обозначениями: либо точный, либо в масштабе, либо иллюстрирующего характера.

6.В геометрических задачах связанных с нахождением длин отрезков, величин углов, площадей фигур и др. геометрических величин все числовые данные приводятся в краткой записи условия, в редких (!) случаях дублируются и на чертеже.

7.В задачах теоретического или логического характера ответ должен быть развернутым и аргументированным, т.е. односложного ответа недостаточно.

Требования к чертежам

1.Чертежи должны быть выполнены карандашом аккуратно по линейке, обозначения аккуратно ручкой (основной учебник – параграфы 3, 4, 11, 13, 23, 27-37; наглядная геометрия – параграф 3).

2.Если обозначения не содержаться в условии задания, то их необходимо выбрать самому.

3.Равные отрезки отмечаются на чертежах равным количеством черточек (основной учебник, параграф 5, №88)

4.Равные углы отмечаются равным количеством дуг (основной учебник – параграф 30, наглядная геометрия – параграф 3).

Требования к буквенным выражениям

1. В записи буквенных выражений числовой множитель ставиться на первое место (перед буквой), знак умножения лишь подразумевается: 2x (читается: произведение чисел 2 и x или удвоенное число x), 2z+3y (сумма удвоенного числа z и утроенного числа y).

2. Если буквенное выражение содержит скобки, то:
а) если множитель ставится перед скобкой, знак умножения лишь подразумевается: a(b+3) (произведение числа a и суммы чисел b и 3), 3(x+y) (произведение числа 3 и суммы чисел x и y);
б) если множитель ставится после скобки, знак умножения обязателен: (b+3)×a (произведение суммы чисел b и 3 и числа a), (x+y)×3 (произведение суммы чисел x и y и числа 3).

Форма записи буквенных выражений без знаков умножения более предпочтительная, удобная и сжатая.

Возможное оформление по типам задач.

1. Задачи на составление выражений.

Оформление.

Цена груш – x р. за 1 кг

Цена моркови – у р. за 1 кг

1) x–y = 18-6 = 12 (р.);

2) x:y = 18:6 = 3;

......................................................

6) 2x+3y = 2×18+3×6 = 36+18 (р.);

7) (2x) : (3y) = 36:18=2;

В данной задаче каждое действие является фактически ответом.

2. Задачи на общее количество.

Оформление 1.

? г

Масса клубничного варенья – 850 г

Масса вишнёвого варенья – ? г, в 2 раза больше

Масса сливового варенья – ? г, на 300 г больше

850+850×2+ 850–300=1700+1700–300=3100 (г)

Ответ: 3100 г.

Оформление 2.

? г

Масса клубничного варенья – 850 г

Масса вишнёвого варенья – ? , 850×2=1700 г

Масса сливового варенья – ? , 850–300=550 г

850+1700+ 550=1400+1700=3100 (г)

Ответ: 3100 г.

3. Зависимость между данными и результатом действия.

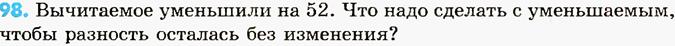
Оформление 1.

Вычитаемое	–52		–52
Уменьшаемое		–52	–52
Разность	–52	+52

Ответ: чтобы разность не изменилась нужно уменьшить вычитаемое на 52.

Оформление 2.

x –вычитаемое; y – уменьшаемое; x-y – разность.

(x–52) – y=(x–y)–52, т.е. разность уменьшится на 52.

x – (y–52)=(x–y)+52, тогда разность увеличится на 52

Ответ: чтобы разность не изменилась нужно уменьшить вычитаемое на 52.

Оформление 3.

При уменьшении вычитаемое на 52 разность уменьшается тоже на 52, тогда чтобы разность не изменилась нужно вычитаемое уменьшить на 52.

4. Задачи на движение.

а) движение по реке:

Оформление 1.

	Скорость (км/ч)	Время (ч)	Расстояние (км)
Катер (по течению)	?
Скорость течения	2
Скорость катера	?

72:4–2=18–2=16 (км/ч)

или

1) 72:4=18 (км/ч) – скорость катера по течению.

2) 18–2=16 (км/ч) – собственная скорость катера

Ответ: 16 км/ч.

Оформление 2 (только краткая запись).

Катер	? км/ч	? км/ч, 4 ч, 72 км
Течение		2 км/ч

Оформление 1.

	Скорость (км/ч)	Время (ч)	Расстояние (км)
Лодка (против течения)	?
Плот	2
Скорость лодки	?

126:7+126:63=18+2=20 (км/ч)

или

1) 126:7=18 (км/ч) – скорость лодки против течения.

2) 126:63=2 (км/ч) – скорость плота (течения).

3) 18+2=20 (км/ч) – собственная скорость лодки.

Ответ: 20 км/ч.

Оформление 2 (только краткая запись).

Лодка	? км/ч	? км/ч, 7 ч, 126 км
Плот (течение)		? км/ч, 63 ч, 126 км

б) встречное движение:

Оформление

(150: (60+15)) 15=30 (км)

или

1) 60+15=75 (км/ч) – скорость сближения мотоциклиста и телеги.

2) 150:75=2 (ч) – время до встречи.

3) 15×2=30 (км) – расстояние до встречи от посёлка.

Ответ: 30 км.

в) движение в противоположные стороны:

Оформление

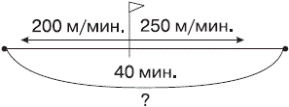
(200+250) 40 = 1800 (м)

или

1) 200+250=450 (м/мин)×– скорость удаления.

2) 450×40=1800 (м)

Ответ: 1800 м.

в) движение в одном направлении:

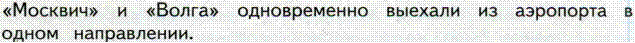
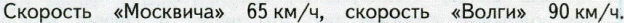
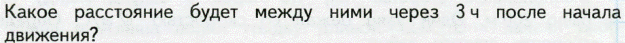
Оформление.

65 км/ч 90 км/ч

3 ч, ? км

(90–65) ×3=75 (км)

или

1) 90–65=25 (км/ч) – скорость обгона.

2) 25×3=75 (км)

Ответ: 75 км.

5. Геометрические задачи.

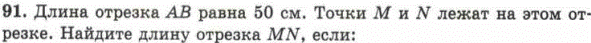
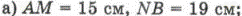
Оформление.

А M N В

Дано: AB=50 см AM=15 см NB=19 см	Решение.   MN=AB–AM–NB=50–19–15=26 (см)   Ответ: 26 см.
Найти: MN

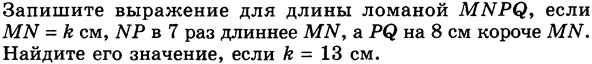
Оформление.

Дано: MNPQ – ломаная MN=k см NP=7k см PQ=k–8 см k=13 см	Решение. lMNPQ= MN+ NP+PQ=k+7k+k–8=9k–8 (см);   9×13–8=117–8=109 (см)   Ответ: 9k–8; 109 см.
Найти: lMNPQ

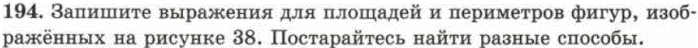
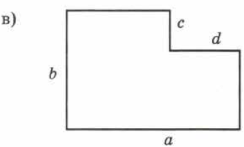
Оформление.

Дано: AB=b CD=c DE=d AF=a	Решение. 1) CC1=DE=A1F=d, C1E=CD=c, AB=C1F=b; BC=AA1=AF– A1F=a–d; EF=C1F–C1E=b–c; I способ: PABCDEF=AB+BC+CD+DE+EF+FA=b+(a–d)+c+d+(b–c)+a= =2a+2b II способ: PABCDEF=PABC1F =AB+BC1+C1F+FA=a+b+a+b=2a+2b 2) SABCDEF=S ABC1F – S CDEC1=AB×AF–CD×DE=a×b – c×d; SABCDEF=S ABCA1 + S A1DEF=AB×AA1– DE×EF=b×(a–d)+d×(b–c) Ответ: PABCDEF=2a+2b; SABCDEF= b×(a–d)+d×(b–c), SABCDEF = a×b – c×d.
Найти: PABCDEF SABCDEF