Аффинные преобразования с использованием однородных координат

В однородных координатах точка 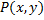записывается как для любого масштабного множителя . При этом если для точки задано ее представление в однородных координатах , то можно найти ее двухмерные декартовы координаты как и .

Геометрический смысл однородных координат состоит в следующем (рис.6). произвольная точка на прямой

Рис. 6. Геометрическая интерпретация однородных координат

Тем самым между производительной точкой с координатами (x, y) и множеством троек чисел вида (W×x, W×y, W), W≠0 устанавливается взаимно однозначное соответствие, позволяющее считать числа W×x, W×y, W новыми координатами этой точки. Таким образом, однородные координаты можно представить как вложение промасштабированной с коэффициентом W двухмерной плоскости в плоскость z = W (здесь z = 1) в трехмерном пространстве.

Применение однородных координат оказывается удобным при решении даже простейших задач.

Если устройство отображения работает только с целыми числами (или если необходимо работать только с целыми числами), то для произвольного значения W (например, W=1) точку с однородными координатами (0,5; 0,1; 2,5) представить нельзя. Однако при разум, ном выборе W можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при W=10 для рассматриваемо­го примера имеем (5; 1; 25).

Другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению, для точки с координатами (80000; 40000; 1000) можно взять, например, W=0,001. В результате получим (80; 40; 1).

Однако основное применение однородных координат — это гео­метрические преобразования, поскольку при помощи троек однород­ных координат и матриц третьего порядка можно описать любое аффинное преобразование в плоскости. Аналогично с помощью чет­верок однородных координат и матриц четвертого порядка можно описать любое преобразование в трехмерном пространстве.

Как известно, преобразования переноса, масштабирования и по­ворота в матричной форме записываются в виде

Р’ = Р + T;

Р’ = Р × S;

Р’ = P × R.

Перенос реализуется отдельно (с помощью сложения) от масшта­бирования и поворота (с помощью умножения). Если выразить точ­ки в однородных координатах, то все три преобразования можно реализовать с помощью умножений. Здесь мы рассмотрим двухмерные преобразования.

Уравнения переноса записываются в виде матрицы преобразования однородных координат следующим образом:

или

Р’ = Р × T(dx, dy),

где

.

Иногда подобные выражения записываются следующим образом:

Рассмотрим, например, двойной перенос точки. Пусть необходи­мо перенести точку Р в точку Р’ на расстояние (dx1, dy1), а затем в P’’ на расстояние (dх2, dу2). Суммарный перенос должен быть равен расстоянию (dх1+d2, dу1+dу2). Запишем данные в виде

P’ = P × T ( dx1, dy1 );

P’’ = P’ × T ( dx2, dy2 ).

Подставляя первую формулу во вторую, получим

P’’ = P × ( T ( dx1, dy1 ) × T ( dx2, dy2 )).

Матричное произведение T ( dx1, dy1) ∙ T ( dx2, dy2 ) есть

Таким образом, результирующий перенос есть (dx1+dx2, dy1+dy2), т.е. последовательные переносы являются аддитивными.

Уравнения масштабирования в матричной форме с использованием однородных координат записываются в виде

,

.

P’ = P’ × S(Sx, Sy).

Матричное произведение S(Sx1, Sy1) × S(Sx2, Sy2) есть

Таким образом, последовательные масштабирования мультипликативны.

И наконец, уравнение поворота ( в правосторонней системе ) можно представить в виде

.

P’ P × R(A).

Последовательные повороты являются аддитивными.

Композиция двухмерных преобразований с помощью однородных координат. Матричное произведение в разных случаях называют объединением, соединением, конкатенацией и композицией. Будем пользоваться последним из перечисленных терминов.

Рассмотрим, например, поворот объекта относительно некоторой произвольной точки P1. Поскольку нам известно лишь как поворачивать вокруг начала координат, разобьем исходную задачу на три подзадачи:

- перенос, при котором точка P1 перемещается в начало координат;

- поворот;

- перенос, при котором точка из начала координат возвращается в первоначальное положение P1.

Последовательность этих преобразований показана на рис. 7.1.

Рис. 7.1. Поворот объекта относительно некоторой произвольной точки

Результирующее преобразование имеет вид

Используя аналогичный подход, можно промасштабировать объект относительно произвольной точки P1: перенести P1 в начало координат, промасштабировать, перенести назад в точку P1. Результирующее преобразование в этом случае будет иметь вид

Рассмотрим более сложное преобразование. Предложим, что нам необходимо промасштабировать, повернуть и расположить в нужном месте объект (домик на рис. 7.2), где центром поворота и масштабирования является точка P1.

Рис. 7.2. пример последовательности преобразования

Последовательности преобразований заключается в переносе точки P1 в начало координат, проведении масштабирования и поворота, а затем переносе из начала координат в новую позицию P2. В структуре данных прикладной программы, в которой содержится это преобразование, могут находиться масштабный множитель (множители), угол поворота и величины переноса или может быть записана матрица результирующего преобразования:

T ( -x1, -y1 ) × S ( Sx, Sy ) × R ( A ) × T ( x2, y2 ).

В общем случае перемножение матриц некоммутативно. Если М1 и М2 представляют собой элементарные перенос, масштабирование или поворот, в следующих частных случаях коммутативность имеет место:

M1	M2
Перенос Масштабирование Поворот Масштабирование (при Sx=Sy)	Перенос Масштабирование Поворот Поворот

Композиция наиболее общего вида, составленная из операций R, S и T, имеет матрицу

Ее верхняя часть размером 2 × 2 является объединенной матрицей поворота и масштабирования, в то время как tx и ty описывают суммарный перенос. Для вычисления Р∙М как произведения вектора на матрицу размером 3 × 3 требуются 9 операций умножения и 6 операций сложения. Структура последнего столбца обобщенной матрицы позволяет упростить фактически выполняемые действия:

x’ = x × r₁₁ + y r₁₁ + t_x,

y’ = x × r₁₂ + y × r₂₂ + t_y,

сводя процесс к 4 операциям на то что матрицы размером 3 × 3 удобны и полезны для совмещения преобразований, в программе целесообразно использовать результирующую матрицу с учетом особенностей ее структуры. Если же умножение матриц выполняется аппаратно с помощью параллельно работающих сумматоров и умножителей (или систолических процессов), то вопрос эффективности перестает быть актуальным.