Типовые практические задания

Вопросы к дифференцированному зачету по дисциплине

««Математика»

для специальности 230401 «Информационные системы»

Семестр

1. Комплексные числа. Действия над комплексными числами.

2. Геометрическая интерпретация комплексного числа.

3. Тригонометрическая форма комплексного числа. Действия над ними.

4. Показательная форма комплексного числа.

5. Определение матрицы, правила, действия над матрицами

6. Определители, свойства определителей

7. Обращение квадратных матриц.

8. Формулы Крамера.

9. Системы линейных уравнений. Матричный метод решения систем линейных уравнений.

10. Метод Гаусса.

11. Векторы. Действия над векторами. Координаты вектора.

12. Действия над векторами в координатах.

13. Векторное произведение.

14. Смешанное произведение векторов.

15. Уравнение линии на плоскости. Уравнения прямой

16. Угол между прямыми.   17. Взаимное расположение двух прямых на плоскости

18. Кривые второго порядка. Окружность.

19. Кривые второго порядка. Эллипс.

20. Гипербола.

21. Парабола.

22. Предел функции. Производная функции.   23. Геометрический смысл производной.   24. Физический смысл производной.

25. Правило Лопиталя. Первый замечательный предел.

26. Асимптоты графика функции.

27. Монотонность функций.   28. Точки экстремума.

29. Выпуклость графиков функций.   30. Вогнутость графиков функций   31. Точки перегиба.

32. Построение графиков функций

33. Неопределенный интеграл. Его свойства.

34. Метод непосредственного интегрирования.   35. Метод замены переменной.

36. Метод интегрирования по частям.

37. Определенный интеграл. Его свойства.

38. Вычисление определенного интеграла

39. Приложения определенного интеграла.

40. Несобственные интегралы.

41. Дифференциальные уравнения первого порядка. Задача Коши.

42. Однородные линейные уравнения первого порядка.

43. Дифференциальные уравнения второго порядка.

44. Числовой ряд.   45. Признак Даламбера.

46. Знакопеременные и знакочередующиеся ряды. Признак Лейбница.

47. Степенные ряды.

48. Функции нескольких переменных.

49. Частные производные и дифференциал функции нескольких переменных.

50. Экстремумы функции нескольких переменных

51. Двойные интегралы. Их свойства.

Типовые практические задания

1. Найдите вторую производную функции y = e^x − x e^x.

2. Найти интервалы выпуклости и точки перегиба графика функции: y = x³ + 3x²

3. Исследовать функцию на точки перегиба y = х³ -3х² + 3х +2

4. Исследовать функцию на монотонность y = 2х³ + 8х² + 12х + 5

5. Исследовать функцию на монотонность, экстремумы: y = х³ − 12х + 11

6. Найти производную функции y = 2 ln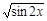

7. Исследовать функцию на точки перегиба y = х⁵ -х³ - 2х

8. Исследовать функцию на монотонность y = - 3х² + 12х

9. Найти производную функции y = ln ln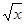

10. Исследовать функцию на монотонность y = - х² + 2х

11. Найти производную функции y = е^-х 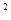ln x

12. Найти точки экстремума функции y 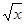= х -6х

13. Найти первую производную функции y = cos² x

14. Найти интервалы выпуклости и точки перегиба графика функции:y = x³ −6x² +x

15. Исследовать функцию на монотонность, экстремумы: y = х³ + 5х + 6.

16. Определить асимптоты кривых. Функция y =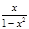

17. Вычислите производную функции y =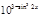

18. Вычислите производную функции y = ln tg 5x

19. Найти интервалы выпуклости и точки перегиба графика функции: y = 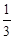x³ − 4x

20. Вычислить первую производную функции y = ln (x² + 2x)

Вычислить:

1.

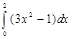
2.

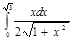
3.

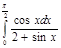
4.

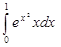
5.

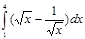
6.

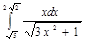
7.

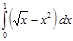
8.

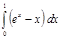
9.

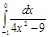
10.

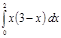
11.

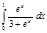
12.

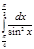
13.

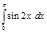
Найти:

1.

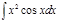
2.

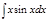
3.

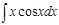
4.

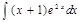
5.

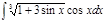
6.

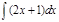
7.

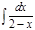
8.

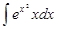
9.

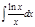
10.

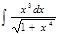
11.

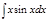
12.

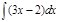
13.

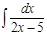
14.

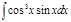
15.

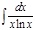
16.

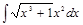
Решите систему уравнений:

1.

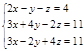
2.

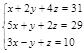
3.

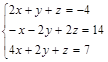
4. Найдите матрицу, обратную данной В =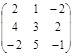

5. Найти матрицу, обратную данной А =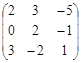

6. Найти матрицу, обратную данной А =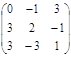

7. Найти произведение матриц А = 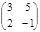и В =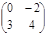

8. Найти 3А − 2В, если А = 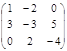, В =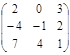

9. Вычислить +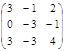

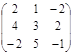
10. Вычислить 2 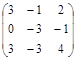- 5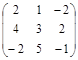

1. Вычислите объем фигуры, образованной вращением площадей, ограниченных указанными линиями y = − x² − x и y = 0 вокруг оси Ох

2. Вычислите объем фигуры, образованной вращением площадей, ограниченных указанными линиями y = x² − 9 и y = 0 вокруг оси Ох

Преподаватель
	Подпись	И.О. Фамилия.