Опертых пластин

Как уже отмечалось, исследование изгиба абсолютно жестких пластин сводится к интегрированию дифференциального уравнения

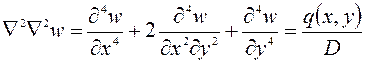(176)

Уравнение (176) представляет дифференциальное уравнение в частных производных с постоянными коэффициентами.

Интегрирование таких уравнений будем производить методом разделения переменных, используя для этой цели тригонометрические функции.

Рассмотрим пластину, все четыре кромки которой свободно оперты на жесткий контур. В этом случае упругая поверхность пластины на опорном контуре должна удовлетворять условиям (см. § 7)

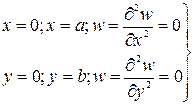(177)

Будем искать решение дифференциального уравнения (176) в виде ряда

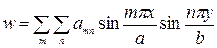(178)

где а_mn — неизвестные коэффициенты, подлежащие определению.

Выражение (178) удовлетворяет граничным условиям (177). Представляя нагрузку q(х, у) в виде двойного ряда Фурье

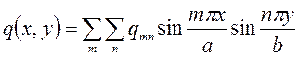(179)

и подставляя выражения (178) и (179) в дифференциальное уравнение (176), получим

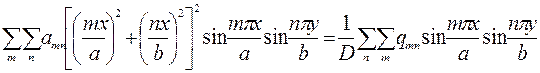(180)

Приравнивая коэффициенты при произведении синусов в левой и правой части, найдем

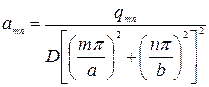(181)

так что общее выражение для стрелки прогиба будет

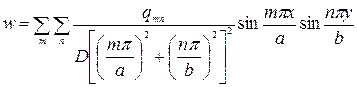(182)

Элементы изгиба пластины могут быть определены по формулам § 4.

Для определения коэффициентов разложения нагрузки q(х, у) в двойной тригонометрический ряд воспользуемся общим методом разложения функции в ряды Фурье.

Умножая обе части равенства

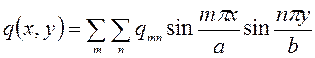(183)

на произведение 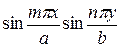и интегрируя в пределах от

«О» до «a2 и от «О» до «b», получим

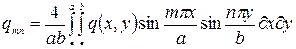(184)

Так, в случае действия на пластику нагрузки, изменяющейся по закону

,

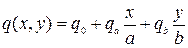нетрудно получить следующую формулу, определяющую коэффициенты q_mn

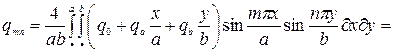
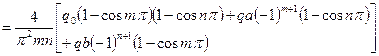(185)