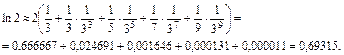Разложение функции в ряд Тейлора

Если функция f(x) имеет производные всех порядков в окрестности точки x=a, то для нее можно написать ряд по степеням (x-a):

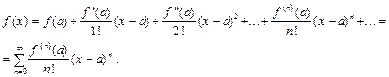
Этот ряд называется рядом Тейлора функции f(x) в точке x=a.

Теорема 6. Если функция f(x) и все ее производные ограничены на интервале (a-R, a+R) одним и тем же числом, т.е. существует постоянная M>0 такая, что выполняется неравенство 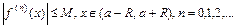, то функция f(x) представляется сходящимся к ней рядом Тейлора:

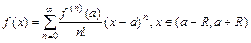. (13)

Равенство (13) верно и в случае, когда остаточный член ряда Тейлора 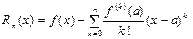стремится к нулю при n®¥. Остаточный член R_n(x) можно вычислить по формуле:

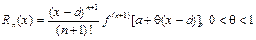. (14)

Если 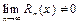, то ряд не сходится к данной функции.

Если в ряде Тейлора положим a=0, получим частный случай ряда Тейлора, который называют рядом Маклорена:
.

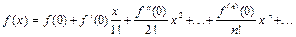Приведем разложения в ряд Маклорена некоторых элементарных функций:

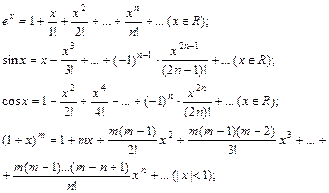
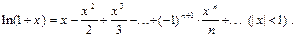
Пример 1. Разложить функцию 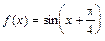в ряд Тейлора в окрестности точки x=0.

Решение. Имеем 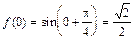. Вычисляем 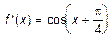, т.е. 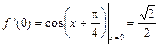. Далее последовательно получаем:

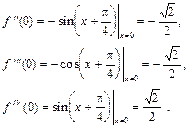
Отметим, что 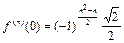. Записываем ряд Тейлора:

Пример 2. Разложить функцию 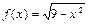в ряд по степеням x, используя разложения основных элементарных функций. Воспользуемся приведенным выше биномиальным разложением 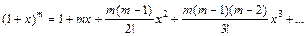. (15)

Преобразуем исходную функцию: 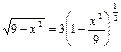. Подставим в формулу (15) 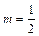, а вместо x выражение 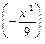. Получим следующее разложение:

Разложение имеет место при 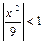, т.е. при |x|<3.

Применение степенных рядов в приближенных вычислениях

Приближенное вычисление значений функций.

Пусть функция f(x) в окрестности точки a разлагается в ряд Тейлора. Тогда приближенное значение функции f(x) в любой точке этой окрестности может быть вычислено как частичная сумма этого ряда.

Пример 1. Вычислить 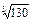с точностью до 0,001.

Решение. 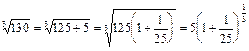. Воспользуемся биномиальным рядом (15) при 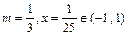. Получаем:

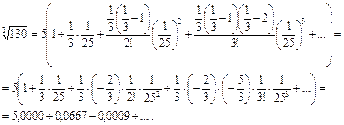
Полученный ряд является знакочередующимся рядом. Третий член по модулю меньше 0,001, поэтому его и следующие за ним члены можно отбросить. С указанной точностью получим .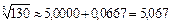

Пример 2. Вычислить 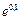с точностью до 0,001.

Решение. Воспользуемся разложением

,

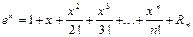где 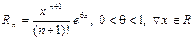. При x=0,1 получаем: 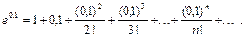Определим, сколько надо слагаемых для достижения требуемой точности. Так как 0,1Î[0,0,5], то 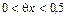. Тогда 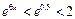; 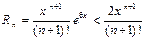. При x=0,1 имеем неравенство: 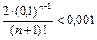. Полагая n=2, получим 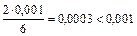. Значит, достаточно взять три слагаемых: .

Пример 3. Вычислить ln2 с точностью до .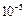

Решение. Применим разложение . Этот ряд сходится при
xÎ(-1,1). Если 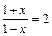, то x=1/3. Возьмем n-ю частичную сумму . Погрешность этого равенства выражается остатком ряда 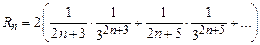. Для его оценки все множители в знаменателях, стоящие перед степенью 3, заменим на 2n+3. Получим

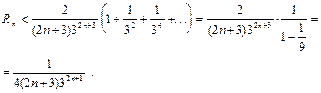
Решая неравенство 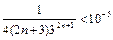, находим, что n=4: 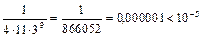. Итак,