Теорема о сложении скоростей – абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей точки.

Составное (сложное) движение точки

Сложное движение точки – такое движение, при котором точка участвует одновременно в двух или нескольких движениях.

Примеры сложного движения точки (тела): лодка, переплывающая реку; человек, идущий по движущемуся эскалатору; камень подвижной кулисы, поршень качающегося цилиндра

Рассмотрим тело, которое свободно движется по отношению к неподвижной системе координат Оxyz. Пусть точка М совершает движение по поверхности этого тела. Через произвольную точку О₁ движущегося тела проведем неизменно связанные с этим телом оси x₁ , y₁, z₁ . Систему осей О₁ x₁ y₁ z₁ называют подвижной системой отсчета.

Движение точки М по отношению к неподвижной системе отсчета называют абсолютным движением точки.

Абсолютное движение ( a ) - движение точки, рассматриваемое относительно неподвижной системы отсчета. Абсолютное движение точки характеризуется изменением радиуса-вектора по модулю и направлению. Абсолютная скорость(ускорение)точки v^a( a^a ) - скорость (ускорение) точки, вычисленная относительно неподвижной системы отсчета.

Относительное движение ( r ) - движение точки, рассматриваемое относительно подвижнойсистемы отсчета.Относительная скорость(ускорение)точки v^r(a^r ) – скорость (ускорение) точки, вычисленная относительно подвижной системы отсчета.

Переносное движение ( e ) - движение подвижной системы отсчета, рассматриваемое относительно неподвижной системы отсчета.

Переносная скорость (ускорение)точки v^e (a^e) – скорость (ускорение) точки, принадлежащей подвижной системе координат или твердому телу, с которым жестко связана подвижная система координат, совпадающейс рассматриваемой движущейся точкой в данный момент времени и вычисленная относительно неподвижной системы отсчета.

К - неподвижная система отчета; К₁ - подвижная система отчета.

Для пояснения сказанного, рассмотрим движение человека по палубе идущего катера.

Неподвижную систему свяжем с берегом реки.

Подвижную систему отчета совместим с движущимся катером.

Движение человека по палубе – относительное движение.

Движение самой палубы – переносное движение.

Движение человека относительно берега – абсолютное движение.

Теорема о сложении скоростей – абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей точки.

Пусть точка М совершает сложное движение.

Положение точки М определяется по отношению к неподвижной системе отчета радиус-вектора .

,

По отношению к подвижной системе отчета положение точки М определяется радиус-вектором .

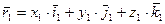
Положение точки О₁ по отношению к неподвижной системе.

Из рисунка имеем

(1)

Дифференцируем векторное равенство (1) по времени t, получим

,

где - абсолютная скорость точки.

(2)

Формула вида (2) или (2^/) выражают теорему параллелограмма сложения скоростей.

Модуль абсолютной скорости найдем по теореме косинуса.

,