Обобщенная модель регрессии

При несоблюдении основных предпосылок обычного метода наименьших квадратов приходится корректировать модель: изменять ее форму, добавлять или, наоборот, исключать факторы, преобразовывать исходные данные и т.п. Особенно часто на практике приходится сталкиваться с ситуациями, в которых не выполняются предпосылки 3 и 4 о том, что возмущения модели имеют постоянную дисперсию и не коррелированны между собой.

Невыполнение предпосылки 3, т.е. нарушение условия гомоскедастичности возмущений (8), означает, что дисперсия возмущения зависит от значений факторов. Такие регрессионные модели называются моделями с гетероскедастичностью возмущений. Например, при исследовании зависимости стоимости туристической путевки (переменная Y) от среднемесячного дохода клиента турагенства (фактор X) можно ожидать, что для более обеспеченных клиентов разброс расходов на отдых выше, чем для менее обеспеченных, т.е. дисперсия возмущений не будет одинаковой для разных значений фактора X (рис. 1).

рис. 1. Линейная модель регрессии с гетероскедастичностью возмущений

Если имеет место гетероскедастичность возмущений, то оценки параметров модели (1) обычным методом наименьших квадратов не будут эффективными, т. е. их дисперсии не будут наименьшими. Рассчитанные значения стандартных ошибок коэффициентов уравнения регрессии (2) могут быть заниженными, а при проверке статистической значимости коэффициентов может быть ошибочно принято решение об их значимом отличии от нуля, тогда как на самом деле это не так.

При малом числе наблюдений, что характерно для эконометрических исследований, для выявления гетероскедастичности может использоваться метод Голдфельда–Квандта. Данный тест используется, если предполагается, что возмущения регрессионной модели распределены по нормальному закону, а среднее квадратическое отклонение возмущений (i=1, 2, …, n) возрастает пропорционально значению фактора. Проверка проводится для всех факторов, включенных в модель, либо только для факторов, предположительно влияющих на однородность исследуемой совокупности. Проверка по некоторому фактору X_j выполняется в следующей последовательности:

1. Все n остатков упорядочиваются по возрастанию значений фактора X_j.

2. В упорядоченном ряду выбирают k первых и k последних остатков, при этом k должно быть больше числа факторов, включенных в модель. Обычно принимают . Центральные остатки, таким образом, исключаются из рассмотрения.

3. По каждой из групп выбранных остатков определяется сумма их квадратов: и .

4. Рассчитывается F-статистика Фишера по формуле , если SS₁>SS₂, или по формуле , если SS₂>SS₁.

5. Статистическая гипотеза об одинаковой дисперсии возмущений не отклоняется, если F-статистика не превышает табличное значение F-критерия Фишера для принятого уровня значимости a и чисел степеней свободы числителя и знаменателя , где р — число факторов в модели (см. приложение).

Предпосылка 4 [условие (10)] может не выполняться при построении регрессионной модели по временным рядам исследуемых переменных, где ввиду наличия тенденции последующие уровни ряда могут зависить от предыдущих уровней. В таком случае говорят, что в модели имеется автокорреляция возмущений. Другими причинами автокорреляции являются:

Ø неучет в модели какого-либо важного фактора;

Ø неправильный выбор формы регрессионной зависимости;

Ø наличие ошибок измерения результативного признака;

Ø цикличность значений экономических показателей;

Ø запаздывание изменения значений показателей по отношению к изменению экономических условий.

При наличии автокорреляции возмущений обычный метод наименьших квадратов дает несмещенные и состоятельные оценки параметров модели, которые однако неэффективны, т. е. их дисперсии не будут наименьшими. По сравнению с гетероскедастичностью возмущений автокорреляция приводит, наоборот, к завышению стандартных ошибок коэффициентов уравнения регрессии. На основе таких результатов может быть сделан ошибочный вывод о несущественном влиянии исследуемого фактора на зависимую переменную, в то время как на самом деле влияние фактора на нее значимо.

Автокорреляция возмущений бывает положительной или отрицательной. Положительная автокорреляция проявляется в том, что завышенные значения возмущений предыдущих наблюдений результата Y приводят к завышению возмущений последующих наблюдений. На графике временного ряда остатков регрессии это выражается, например, в чередовании зон положительных и отрицательных остатков (рис. 2). При отрицательной автокорреляции, наоборот, завышенные значения возмущений предыдущих наблюдений занижают возмущения последующих наблюдений, а остатки регрессии «слишком часто» меняют знак (рис. 3).

Автокорреляцию возмущений выявляют путем исследования ряда остатков с помощью разных критериев. Наиболее часто для этой цели используется тест Дарбина–Уотсона, основанный на предположении, что если имеется автокорреляция возмущений, то она присутствует и во временном ряду остатков регрессии. Тест основан на расчете d‑статистики

,

(20)

значение которой сравнивают с критическими значениями d₁ и d₂ (см. приложение). При этом могут возникнуть следующие ситуации:

· если , то возмущения признаются некоррелированными;

· если 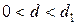, то имеется положительная автокорреляция возмущений;

· если , то существует отрицательная автокорреляция;

· если или , то это указывает на неопределенность ситуации.

В последнем случае для выявления автокорреляции используется коэффициент автокорреляции остатков первого порядка

.

(21)

Статистическая гипотеза об отсутствии автокорреляции возмущений не отклоняется на принятом уровне значимости a, если коэффициент автокорреляции не превышает по абсолютной величине критическое значение (см. приложение). В противном случае делают вывод об автокорреляции возмущений: положительное значение коэффициента автокорреляции указывает на положительную автокорреляцию, а отрицательное — соответственно на отрицательную.

рис. 2. Модель регрессии с положительной автокорреляцией возмущений

рис. 3. Модель регрессии с отрицательной автокорреляцией возмущений

Невыполнение предпосылок 3 и 4 означает, что ковариации и дисперсии возмущений могут быть произвольными, т. е. задаваться некоторой положительно определенной матрицей W:

,

(22)

где W — ковариационная матрица вектора возмущений.

Модель множественной регрессии, для которой выполняется условие (22), называется обобщенной линейной моделью множественной регрессии (Generalized Linear Multiple Regression Model). Для получения несмещенных и наиболее эффективных оценок параметров такой модели применяют обобщенный метод наименьших квадратов (Generalized Least Squares), условие которого имеет вид:

.

(23)

Вектор оценок b* параметров обобщенной модели определяется как

.

(24)

Следует заметить, что коэффициент детерминации R² для обобщенной модели не является удовлетворительной мерой ее качества и может использоваться лишь как приближенная характеристика модели.

На практике ковариационная матрица вектора возмущений W, как правило, неизвестна, и для реализации обобщенного метода наименьших квадратов приходится вводить дополнительные условия на структуру матрицы W. Поэтому устранение гетероскедастичности и автокорреляции возмущений производят раздельно, для чего используют частные случаи обобщенного метода наименьших квадратов.