Тест егэ - 2017 по математике

ПРОФИЛЬНЫЙ УРОВЕНЬ

ВАРИАНТ 3

Часть 1

1. В доме, в котором живёт Женя, один подъезд. На каждом этаже по восемь квартир. Женя живёт в квартире 87. На каком этаже живёт Женя?

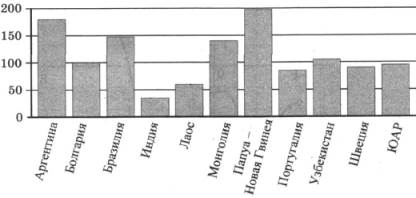
2. На диаграмме показано распределение выплавки меди в 11 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимала Папуа - Новая Гвинея, одиннадцатое место - Индия. Какое место занимал Узбекистан?

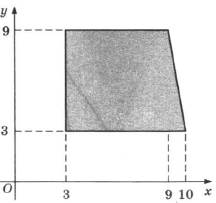
3. Найдите площадь прямоугольной трапеции, вершины которой имеют координаты (3; 3), (10; 3), (9; 9), (3; 9).

4. В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос о Великой Отечественной войне. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о Великой Отечественной войне.

5. Найдите корень уравнения

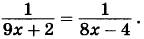
6. Угол А четырёхугольника ABCD, вписанного в окружность, равен 25°. Найдите угол С четырёхугольника. Ответ дайте в градусах.

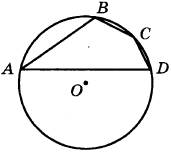
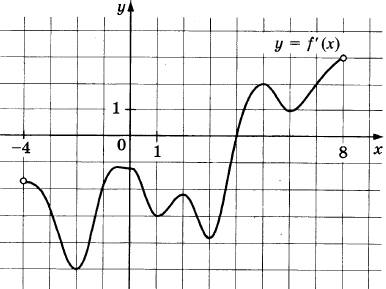
7. На рисунке изображён график производной у = f'(x) функции f(x), определённой на интервале (−4; 8). В какой точке отрезка [−3; 1] функция f(x) принимает наименьшее значение?

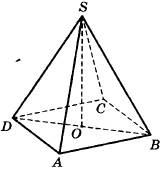
8. В правильной четырёхугольной пирамиде SABCD точка О - центр основания, S - вершина, SA = 10, BD = 16. Найдите длину отрезка SO.

Часть 2

9. Найдите значение выражения

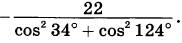
10. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением pV^1,4 = const, где р (атм) - давление в газе, V - объём газа в литрах. Изначально объём газа равен 256 л, а его давление равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде поднялось до 128 атмосфер? Ответ выразите в литрах.

11. Плиточник должен уложить 300 м² плитки. Если он будет укладывать на 5 м² в день больше, чем запланировал, то закончит работу на 5 дней раньше, чем наметил. Сколько квадратных метров плитки в день планирует укладывать плиточник?

12. Найдите точку максимума функции

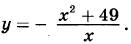
13. а) Решите уравнение tg²x + 5tg x + 6 = 0.

б) Найдите все корни этого уравнения, принадлежащие отрезку

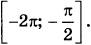
14. Ребро SA пирамиды SABC перпендикулярно плоскости основания АВС.

а) Докажите, что высота пирамиды проведённая из точки А, делится плоскостью, проходящей через середины рёбер АВ, АС и SA, пополам.

б) Найдите расстояние от вершины А до этой плоскости, если SA = √5, AB = AC = 5, BC = 2√5.

15. Решите неравенство

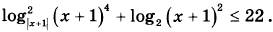
16. Точки В₁ и С₁ лежат на сторонах соответственно АС и АВ треугольника АВС, причём АВ₁ : В₁С = АС₁ : С₁В. Прямые ВВ₁ и СС₁ пересекаются в точке О.

а) Докажите, что прямая АО делит пополам сторону ВС.

б) Найдите отношение площади четырёхугольника АВ₁ОС₁ к площади треугольника АВС, если известно, что АВ₁ : В₁С = АС₁ : С₁В = 1 : 4.

17. Тимофей хочет взять в кредит 1,1 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Тимофей взять кредит, чтобы ежегодные выплаты были не более 270 тысяч рублей?

18. Найдите все значения а, при каждом из которых уравнение

64х⁶ + 4х² = (3х + а)³ + 3х + а

не имеет корней.

19. Конечная последовательность а₁, а₂, ... , а_n состоит из n ≥ 3 не обязательно различных натуральных чисел, причём при всех натуральных k ≤ n − 2 выполнено равенство

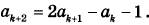
а) Приведите пример такой последовательности при n = 5, в которой а₅ = 4.

б) Может ли в такой последовательности некоторое натуральное число встретиться три раза?

в) При каком наибольшем n такая последовательность может состоять только из трёхзначных чисел?

Ответы:

выбрать другой вариант