Влаж. воздух. Способы задания его парам-ов. Абсол. и относ. влажность

h, кДж/кг

Атмосф возд - всегда смешан с водян паром: Такая смесь сухого возд с водяным паром наз влажным возд. Однако кол-во водяного пара в газов смеси не м б произвольным. В зав-ти от т-ры и полного давлениясмеси кол-во водяного пара во влажном воздухе не мож превышать определ велич.Тк в пр-х изм-я физич состояния влажного воздуха состав сухого воздуха не изменяется, его мож считать одним из компонентов паровоздушн смеси, несмотря на то, что в действит-ти он сам явл-ся смесью газов. Вторым компонентом влажного воздуха явл-ся водяной пар. Возм-ть фазового перехода у одного из компонентов смеси (воды) отличает влаж возд от обычной газов смеси. Кроме водяного пара влажн возд мож содержать мельчайш капельки воды(в виде тумана) или кристаллики льда. Водяной пар во влаж воздухе мб в перегретом или насыщенном состоянии. Парциаль давление водяного пара р_п во влаж воздухе не м б выше давления насыщения р_н при данной т-ре влажн возд (р_п ≤ p_н). Наибольшее зн-е парциального давления водяного пара во влажном воздухе р_H определяется только т-рой смеси и не зависит от давления смеси р. Смесь сухого воздуха с перегретым водяным паром называется ненасыщ влаж воздухом. Для такой смеси справедливо условие р_п < p_н. Смесь сухого воздуха с насыщ водяным паром называется насыщ влажным возд. В насыщ влаж воздухе р_п = p_н. Понижая т-ру насыщ влажн воздуха при р=const, мож охладить воздух до такой т-ры, при кот парциальное давление водяного пара будет соотв-ть состоянию насыщения, и при дальнейшем понижении т-ры из воздуха начнет выделяться влага. Так, напр, понижение т-ры атмосф воздуха часто приводит к появлению тумана(к конденсации пара). При давлениях, близких к атмосферному, газовая смесь, состоящая из воздуха и водяного пара, по своим св-вам мало отличается от св-в ид газа. Парциаль давл водяного пара в воздухе обычно мало, поэтому и водяной пар при этих условиях мож считать ид газом. Масса водяного пара, содержащегося в 1 м³ влажного воздуха, наз абс влажностью. Тк влажный воздух представляет собой газов смесь, то объём водяного пара в смеси равен объему всей смеси и, сл-но, абс влажность равна парциальной плотности пара r'_п в смеси при своем парциальном давлении р_п и т-ре смеси: r'_п = m_п/V=p_п/(R_пT). Отношение абс влаж воздуха r'_п к максимально возможной абс влажности r'_н при данной т-ре называется относит влажностью. Так как для ид газов в условиях T = const отнош-е плотностей мож заменить отнош-ем давлений, то относит влаж j = r’_п/r’_н = p_п/p_н,где р_п и р_н— парциальные давления водяного пара во влажном воздухе и насыщенного пара при т-ре влажного воздуха. Относит влаж обычно выр-ся в процентах и изменяется в пределах 0<j<100%, так как пределы изменения парциального давления пара 0£p_п£р_н. Для сухого воздуха j = 0, для насыщенного j= 100%. Для определения содержания пара во влажном воздухе, помимо относительной влажности j, необходимо знать т-ру влаж возд, по кот (из паровых таблиц) определяется давление насыщенного пара р_н. Абс влажность воздуха r'_п = jr'_н.

35.Дифференц ур тд устанавливают кол-ные хар-ки м\у различными физич св-ми в-ва, вытекающих из основных зак тд-ки. В случае, когда часть параметров оказывается известной, остальные параметры мб найдены путем интегрирования соответствующих диф-х ур.

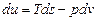(1)

Независимые переменные v и Т:

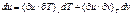-для внутренней энергии (2)

Частные производные входящие в это выражение можно найти ч/з термодинамические параметры и их проихводные. Так из (1) следует, что при Т=const

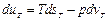,откуда

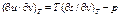(3)

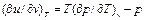(4)

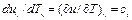(5) ,подставляем (4) и (5) в (2)

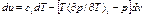(6)

Диф ур для энтропии мож получить совместно решая уравнеия (1) и (6)

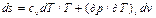
Независимые переменные р и Т: Энтальпия является функцией состояния, поэтому:

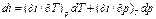
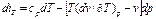
Дифференциалы характеристич-х функций в математич смысле явл-ся полными дифференциалами, а ур вида dψ=(δψ/δx_k)_xldx_k+(δψ/δx_l)_xkdx_l представляют собой линейные дифференциальные соотношения. Согласно св-ву полного дифференциала, 2производная от фун ψ не зависит от порядка дифференцирования δ/δxl(δψ/δx_k)=δ/δx_k(δψ/δx_l). В соответсвии с этим соотношением смешанные производные, напр, производные от внутренней Е, мож записать в виде (δ/δx_l(δu/δs)_ν)_s=(δ/δs(δu/δν)_s)_ν, или после замены частных производных (δu/δs)_ν и (δu/δν)_s через т/д-ские параметры получается (δT/δν)_s=-(δp/δs)_ν. Также (δT/δp)_s=(δν/δs)_p; (δs/δν)_T=(δp/δT)_ν; (δs/δp)_T=-(δν/δT)_p. Эти последние 4 уравнения наз-ся дифференциальными соотношениями т/д-ки или соотношениями взаимности Максвелла и широко испо-ся в т/д-ском анализе.Эти соотношения, являясь следствием 1-го и 2-го законов т/д-ки, в такой же степени достоверны, как и сами основные законы

36. Вл.возд. Расчет т/д парам-ов вл. возд. (молярка, плотность, газ.пост., теплоемкость, энтал).

Объемные доли сухого возд и пара во влажном воздухе Мб определены, если известны парциальные давления пара и сухого воздуха, отношениями r_B = p_B/р = (р -р_п)/р, r_П = p_П/р, где в соответствии с законом Дальтона р = р_В + р_П. При известных объемных долях кажущаяся молярная масса влаж воздуха мб вычислена по формуле M = M_Br_B + M_Пr_П = [28,96(р - р_п)/ р] +18,016 p_П/р. Если учесть, что р_П = j p_H, и принять водяной пар, находящийся во влажном воздухе, в качестве ид газа, то М = 28,96—10,94j p_H/p. При заданном давлении влаж возд кажущаяся молярная масса влажн возд зав-т от т-ры и относит влаж воздуха. тк газов постоянная смеси газов R = 8314/M, газ постоянную возд мож определить отношением R = 8314/(28,96— 10,94p_П/p) = 8314/(28,96—10,94j p_H/p).При j = 0 (соответствует сухому воздуху) R = R_B = 287 Дж/(кг*К). В др предельном случае при j = 1 (соответствует чистому водяному пару) p_H = p, a R = R_П = 461 Дж/(кг*К). Газов постоянная влаж возд всегда больше газов постоянной сухого воздуха. Массов доли сухого воздуха и пара во влажном воздухе Мб выражены через влагосодержание так: g_B = (m_B/m) = m_B/(m_B+m_П) = 1/(1+d); g_П = (m_П/m) = m_П/(m_B+m_П) = d/(1+d). Отношение массы m_пводяного пара, содержащегося во влаж воздухе, к массе т_всухого воздуха наз влагосодержанием dвлажного воздуха. Для газов постоянной влаж воздуха мож получить формулу R = (287 + 461d)/(1+d). Ур состояния влажного воздуха мб записано в след форме: р/r = 8314T/(28,96 — 10,94p_П/p), откуда плотность влаж возд r = (28,96р-10,94р_П)/(8314Т). Из полученной формулы следует, что с увелич парциального давления пара (т. е. с увелич влажн воздуха) плотность влаж воздуха уменьш.Поэтому влаж воздух всегда легче, чем сухой. тк плотность влаж воздуха равна сумме парциальных плотностей сухого воздуха и водяного пара, а влагосодерж d = r'_П/r'_B, то r = (r'_П/d)(1+d). Парциальная плотность водяного пара м б вычислена по уравнению состояния r'_П = m_П/V = p _П /(R _П T) = d*p/[0,622+d)R _ПT)] Подставляя значения r'_П в выражение (12.19), окончательно получим r = p(1+d)/[(0,622+d) R _ПT] Теплоемк влаж возд с_р обычно относят к (1+d) кг влажного воздуха (или, что то же самое, к 1 кг сухого воздуха). Она равна сумме теплоемкостей 1 кг сухого воздуха и d кг водяного пара: c_P = c_PB+d*c_PП, где c_PB и c_PП - массовые изобарные теплоемкости сухого воздуха и водяного пара соотв-но. В приближенных тд-ких расчетах, связанных с влажным воздухом, мож принимать c_PB »1 кДж/(кг-К) и c_PП »1,93 кДж/(кг-К). Энтальпия влаж воздуха определяется как энтальпия газов смеси, состоящей из 1 кг сухого воздуха и d кг водяного пара, поэтому h = h_В+d*h_П , где h_В - энтальпия сухого воздуха, h_П - энтальпия водяного пара. При определении энтальпии газов смеси необх, чтобы энтальпии компонентов смеси имели одно и то же начало отсчета. Энтальпия сухого воздуха h_В = c_РВt = t, так как c_PB = 1. Водяной пар в первом приближении мож принять в качестве ид газа, энтальпия кот не зависит от давления. Если кроме того, учесть, что в условиях изменения физич состояния влажного воздуха интервал изменения т-р мал, то мож принять теплоемкость водяного пара постоянной. При этих упрощающих предположениях энтальпия водяного пара может быть вычислена по формуле h_П = r + c_PП t, где r - скрытая теплота парообразования при 0°С. Так как r = 2501 кДж/кг, то h_П = 2501 + 1,93t. Т о h = t + (2501+1,93t)d.Установим зависимость энтальпии влажного воздуха от относит влаж: h = t + (1555+1,2t) jp_H)/(р – jp_H). В общ случае, когда влаж возд помимо водяного пара содержит воду (туман) и лед (снег), в правой части формулы h = t + (2501+1,93t)d появятся еще 2 слагаемых d_Жh_Ж и d_Th_T, в которых d_Ж и d_T - содержание жидкой и твердой фазы во влажном воздухе; h_Ж = c_Жt = 4,l9t и h_T = 2,lt - 335 - энтальпия воды и льда соответственно. В этом случ формула для расчета энтальпии влаж воздуха получит вид h = t + (2501+1,93t)d + 4,l9d_Жt + (2,lt – 335)d_T. При наличии жидкой или твердой фазы влагосодержание d = d_Н.

37. Диф. уравнения т/д. Уравнения взаимосвязи 3-х частных производных.

Необходимость введения харак-х функций в т/д-ку впервые была теоретически обоснована Масье, однако в наиболее строгом и полном изложении метод хар-их функ получил в работах Дж. Гиббса. Гиббс показал, что из всего множ-ва т/д-их фун мож выбрать такие функц, частные производные кот наиболее просто выражаются через т/д-ие параметры. Построение т/д-ого анализа на особых св-вах таких функций и составляет основу метода хар-их функций. В основу построения метода положено обобщенное уравнение 1закона т/д-ки

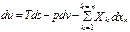
Внутр Е явл-ся функцией состояния, то ее дифференциал обладает св-ми полного диф-ла. Диф-ал получит вид du=(δu/δs)_υds+(δu/δυ)_sdv. (δu/δs)_υ=T, (δu/δυ)_s=-p. Характеристической функцией явл-ся уде энтальпия с независимыми переменными s и p. Полный диф-ал функциональной зависимости i=f(s,p) им вид di=(δi/δs)_pds+(δi/δp)_sdp. ее частные производные (δi/δs)_p=T, (δi/δp)_s=υ. Энтальпия явл-ся характеристической функцией с независимыми переменными s и p. Ур 1 закт/д-ки свидетельствует также, что свободная Е явл-ся характер. функцией с независимыми переменными υ и T. Дифференциал функциональной зав-ти F=f(υ,T) имеет вид dF=(δF/δT)_υdT+(δF/δυ)_Tdυ, а ее частные производные: (δF/δT)_υ=-s, (δF/δυ)_T=-p. Эти все характеристические уравнения связаны с 1 зак т/д

38. Вл.воздух. dh – диаграмма. Кондицир-ие воздуха

Наиболее просто и быстро мож определять парам влажного воздуха, а также проводить исследования термодинамических процессов с влажным воздухом с помощью dh - диагр.

Впервые dh – диагр для влажного воздуха была предложена профессором Л. К. Рамзиным (1918) и нашла широкое прим-е в расчетах систем кондиционирования, сушки, вентиляции и отопления. В dh – диаграмме по оси абсцисс откладывается влагосодерж d (г/кг сухого воздуха), а по оси ординат - уд энтальпия hвлаж воздуха (кДж/кг). При построении dh - диаграммы использована косоугольная система коорд, тк в такой сист обл ненасыщенного воздуха занимает значительно большую площадь диаграммы. Ч\з точки на оси ординат проводят линии h = const под углом а=135° к линиям d = const. После нанесения сетки линий d = const и h = const на диаграмму наносят изотермы (t = const) и кривые j = const.Обычно dh - диаграмму строят для какого-то ср атмосф давления. Пр-с нагрева влаж воздуха на dh-диаграмме изображается вертикальной линией снизу-вверх при d = const. Пр-с охлаждения также протекает при d = const и изображается также вертикальной прямой сверху-вниз. Этот пр-с справедлив только до состояния полного насыщения (j = 100%). при дальнейшем охлаждении воздух будет пересыщен влагой, и она будет выпадать в виде росы. На dh - диаграмме дана схема определения точки росы. С уменьшением т-ры влажного ненасыщенного воздуха при d = const увеличивается j. При j = 100% имеем состояние насыщ влажн воздуха. Т-ру, при кот j = 100%, называют точкой росы. Атмосф возд представляет смесь сухих газов и водяного пара, т. е. является влажным воздухом. Практически неизменной остается лишь сухая часть состава воздуха. Во многих отраслях промышленности практически нельзя работать без создания изолированного климата, без применения так называемого кондиционирования воздуха. Термин «кондиционирование» происходит от латинского слова «condicio», что означает «условие». Путем создания систем кондициониров необх обеспечить определенные знач параметров воздуха, подаваемого в кондиционируемое помещение. Для поддержания заданных параметров воздуха в помещении необходимо при летнем режиме его охлаждать и осушать, а при зимнем режиме — нагревать и увлажнять. Указанные пр-сы при кондиционировании осуществляются в аппаратах, называемых кондиционерами.

39. Диф. уравнения т/д.Частные производные характеристических функций.

Получены 4 характеристических функций : u(s¸υ), i(s¸p), F(T¸υ), G(T¸p). Все эти функции обладают особым свойством – их частные производные по определенным независимым переменным могут быть выражены через сопряженные т/д-ские параметры: (δu/δs)_ν=T, (δu/δν)_s=-p, (δi/δp)_s=ν;(δF/δT)_ν=-s;

(δi/δs)_p=T; (δF/δν)_T=-p; (δG/δT)_p=-s; (δG/δp)_T=ν. Это особое свойство характеристических функций существенно упрощает весь т/д-ский анализ.

Ур-я в частных производных от характеристических функций наз-ся диф ур т/д.Частные производные характеристич функ однозначно определяют физич св-ва в-ва, поэтому диф. ур т/д, отражают связи м\у различными физич эффектами, вытекающие из 1 и 2 законов т/д. Эти ур позволяют выразить величины du, di, ds, входящие в уравнение 1-го закона т/д, через основные т/д-ческие характеристики в-ва. Если рассматривать внутр Е как функцию независимых переменных υ и T, то ее дифференциал можно представить в виде суммы: du=(δu/δT)_υdT+(δu/δυ)_Tdυ.

Частные производные находится через т/д-ские параметры и их производные. При T=соnst du_T=Tds_T-pdυ_T, откуда (δu/δυ)_T=T(δp/δT)_υ-p или (δu/δυ)_T=T(δp/δT)_υ-p ,а производную (δuδT)_υ определяем: du=cdT-pdυ, при υ=const du_υ=c_υdT_υ, отсюда du_υ/dT_υ=(δu/δT)_υ=c_υ. Энтальпия является функцией состояния, поэтому дифференциал функциональной зависимости i=f(p,T) имеет вид di=(δi/δT)_pdT+(δi/δp)_Tdp. Частная производная (δi/δp)_T : di_T=Tds_T+υdp_T, то (δi/δp)_T=T(δs/δp)_T+υ или (δi/δp)_T=-T(δυ/δT)_p+υ. Для (δi/δT)p : δq=c_pδT, где c_p-удельная теплоемкость системы в процессе при постоянном давлении. Знач (δi/δT)_p=c_p. Если в кач-ве независимых переменных выбрать υ и p, то дифференциал удельной внутренней энергии можно представить в виде: du=(δu/δp)_υdp+(δu/δυ)_pdυ.тк (δu/δp)_υ=(δu/δT)_υ(δT/δp)_υ, значит (δu/δp)_υ=c_υ(δT/δp)_υ, а при p=const du_p=c_pdT_p-pdυ_p, откуда (δu/δυ)_p=c_p(δT/δυ)p-p.

41.Диф Ур тд устанавливают кол-ные хар-ки м\у различ физич св-ми в-ва, вытекающих из основных зак тд. В случае, когда часть параметров оказывается известной, остальные параметры Мб найдены путем интегрирования соответствующих дифференциальных уравнений.

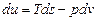(1)

Независимые переменные v и Т:

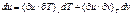-для внутренней энергии (2)

Частные производные входящие в это выражение можно найти ч/з термодинамические параметры и их проихводные. Так из (1) следует, что при Т=const

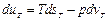,откуда

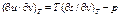(3)

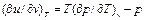(4)

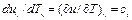(5) ,подставляем (4) и (5) в (2)

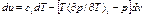(6)

Дифференциальное уравнение для энтропии можно получить совместно решая уравнеия (1) и (6)

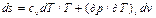
Независимые переменные р и Т: Энтальпия является функцией состояния, поэтому:

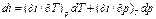
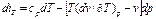
Истинная теплоемкесть отнош кол-ва теплоты dQ в бесконечно малом тд-ом процессе к изменению т-ры dT в том же процессе: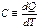

Для конечного процесса 1-2 вводится понятие ср теплоемк как отношения полного кол-ва теплоты Q_I-2 к изменению температуры: .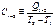

Если сист представляет собой однородное в-во (рабочее тело), то применяют понятия:уд теплоемкости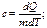

молярной теплоемкости ­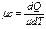

объемной (при н у) теплоемкости ,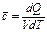

где m- масса; m- количество вещества; V - объем рабочего тела, приведенный к нор­мальным условиям (давление 101325 Па; температура 273,15 К). Единицы этих тепло­емкостей соответственно: Дж/(кг.К),Дж/(кмоль.К) и Дж/(м³.К).

Теплоемк данного раб тела хар-ет не только его собственное физич св-во, но и зависит от того, в каком конкретном тд-ом процессе раб тело получает или отдает энергию в форме теплоты. В зависимости от характера тд-ого процесса, в кот участвует раб тело, его теплоемк может принимать любое значение от + µ до - µ. .

для пр-са при постоянном объеме рабочего тела получаем изохорную теплоемкость: ,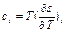

для пр-са при постоянном давлении - изо­барную теплоемкость: .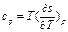

Истинную теплоемк рабочего тела в каком- либо состоянии в ходе данного термодинамического процесса можно определить графичес­ки, построив линию процесса в sT-диаграмме