Интегрирование рациональных дробей
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
Федеральное государственное образовательное учреждение высшего профессионального образования
"Мурманский государственный технический университет"
Кафедра высшей математики
и программного обеспечения ЭВМ
Интегральное исчисление
функции одной переменной.
Дифференциальные уравнения
Часть 3
Методические рекомендации к выполнению контрольных работ
для студентов 1 курса вечерне-заочного факультета
по дисциплине "Математика"
Мурманск
УДК 514.2 + 512.64 + 514.144.2 (075.8)
ББК 22.151.5 + 22.143Я73
М 33
Составители: Великая Елена Евгеньевна, старший преподаватель кафедры высшей математики и программного обеспечения ЭВМ МГТУ;
Мостовская Любовь Григорьевна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ;
Хохлова Людмила Ивановна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой
15 февраля 2006 г., протокол № 4
Рецензент – В.С. Кацуба, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Оригинал-макет подготовлен в авторской редакции
Электронная верстка Е.И. Бабушкиной
© Мурманский государственный
технический университет, 2007
Оглавление
Введение... 4
Методические указания по темАМ
"Интегральное исчисление функции одной переменной"
И "Дифференциальные уравнения". 5
Справочный материал по теме "Интегральное
исчисление функции одной переменной". 6
1. Первообразная и неопределенный интеграл. Таблица интегралов. 6
2. Свойства неопределенного интеграла.
Замена переменной под знаком неопределенного интеграла. 7
3. Интегрирование по частям.. 9
4. Интегрирование рациональных дробей. 9
5. Интегрирование некоторых тригонометрических функций. 9
6. Формула Ньютона-Лейбница. 10
7. Несобственные интегралы первого и второго рода. 11
8. Вычисление площади плоской фигуры
в декартовой системе координат (ДСК) 12
9. Вычисление площади плоской фигуры
в полярной системе координат (ПСК) 12
10. Вычисление объема тела вращения. 12
11. Вычисление длины дуги плоской кривой. 13
Примерный вариант и образец выполнения
контрольной работы 5. 13
Справочный материал по теме
"Дифференциальные уравнения". 20
1. Дифференциальные уравнения 1-го порядка. 20
2. Методы решения основных типов
дифференциальных уравнений 1-го порядка. 21
3. Дифференциальные уравнения 2-го порядка. 27
4. Решение дифференциальных уравнений 2-го порядка,
допускающих понижение порядка. 28
5. Решение линейных дифференциальных уравнений
2-го порядка с постоянными коэффициентами. 32
6. Системы двух линейных дифференциальных уравнений
и их решение порядка методом повышения порядка. 37
Примерный вариант и образец выполнения
контрольной работы 6. 38
Варианты контрольнЫХ работ.. 47
Рекомендуемая литература.. 52
Введение
В настоящем пособии содержатся методические рекомендации к изучению теоретического материала и выполнению контрольных работ по темам "Интегральное исчисление функции одной переменной" и "Дифференциальные уравнения", варианты этих контрольных работ и список рекомендуемой литературы.
В результате изучения этих тем студенты должны:
• изучить основные методы интегрирования – интегрирование методом замены переменной и интегрирование по частям, научиться интегрировать рациональные дроби и тригонометрические функции;
• получить представление об определенном интеграле и его свойствах, научиться вычислять его по формуле Ньютона-Лейбница;
• научиться исследованию несобственных интегралов первого и второго рода на сходимость и расходимость;
• научиться использовать определенный интеграл для решения геометрических задач, таких как вычисление площади плоской фигуры, объема тела вращения, длины дуги плоской кривой.
• знать основные понятия теории дифференциальных уравнений
(порядок дифференциального уравнения, его общее и частное решения, начальные условия и др.) и уметь определять тип дифференциального уравнения;
• знать и уметь использовать методы решения основных типов дифференциальных уравнений 1-го порядка а также дифференциальных уравнений 2-го порядка, допускающих понижение порядка;
• уметь решать линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и системы линейных дифференциальных уравнений 1-го порядка методом повышения порядка.
Данные методические рекомендации включают также справочный материал, необходимый для выполнения контрольных работ по темам "Интегральное исчисление функции одной переменной" и "Дифференциальные уравнения", и подробные решения примерных вариантов работ со ссылками на используемый справочный материал.
Методические указания по темАМ
"Интегральное исчисление функции одной
переменной" И "Дифференциальные уравнения"
В табл. 1 приведены наименования тем в соответствии с содержанием контрольных работ и ссылки на литературу по этим темам. Перед выполнением каждой из контрольных работ рекомендуется изучить соответствующий теоретический материал и решить указанные в таблице задачи.
Таблица 1
| № к. раб. | № задачи | Содержание (темы) | Литература |
| Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица интегралов. Основные методы интегрирования: метод замены переменной, интегрирование по частям | [1], гл. VII, § 29, 30; [3], гл.7, § 1–4; [4], гл. IX, № 1337–1350, 1368–1371, 1373–1375; 1392–1396; [6], гл. 6, № 2–14, 36–50, 102, 103, 108, 109, 114, 118–120 | ||
| Интегрирование рациональных дробей. Интегрирование некоторых тригонометрических функций | [1], гл. VII, § 31, 32; [3], гл.7, § 5, 6.3; [4], гл. IX, № 1410–1416, 1428–1434, 1489–1490, 1494–1505; [6], гл. 6, № 172, 177–180, 193, 194–199, 230–242 | ||
| Определенный интеграл и его свойства. Вычисление определенного интеграла по формуле Ньютона-Лейбница. Несобственные интегралы первого и второго рода | [1], гл. VIII, § 35-40; [3], гл. 8, § 1, 4–9, 11; [4], гл. X, № 1552–1554, 1559–1560; 1572–1578; [6], гл. 6, № 255–266, 355–360, 366–369 | ||
| Приложение определенного интеграла: вычисление площади плоской фигуры | [1], гл. VIII, § 41.1, 41.2; [3], гл. 8, § 10.1, 10.2; [4], гл. X, № 1596–1601; [6], гл. 6, № 290–294, 301, 302 | ||
| Приложение определенного интеграла: вычисление объема тела вращения | [1], гл. VIII, § 41.4; [3], гл. 8, § 10.4; [4], гл. X, № 1628–1631; [6], гл. 6, № 319–323 |
Продолжение табл. 1
| № к. раб. | № задачи | Содержание (темы) | Литература |
| Приложение определенного интеграла: вычисление длины дуги плоской кривой | [1], гл. VIII, § 41.3; [3], гл. 8, §10.3; [4], гл. X, № 1613–1618; [6], гл. 6, № 307–312 | ||
| Дифференциальные уравнения 1-го порядка | [2], гл. I, § 1.1, 1.2, 2.1–2.4; [3], гл. 15, § 1.1–1.6; [5], гл. IV, № 515–517, 550–556, 603–608; [6], гл. 14, № 32–38, 43–54, 61–64, 139–140 | ||
| Дифференциальные уравнения 2-го порядка, допускающие понижение порядка | [2], гл. I, § 3.1, 3.2; [3], гл. 15, § 2.1–2.2; [5], гл. IV, № 651, 652, 654, 659–665 | ||
| Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами | [2], гл. I, § 3.4, 4.1, 5.1–5.3; [3], гл. 15, § 3–4; [5], гл. IV, № 696–699; 721–726; [6], гл. 14, № 98–111, 180, 184, 185 | ||
| Системы линейных дифференциальных уравнений 1-го порядка | [2], гл. I, § 6.1–6.2; [5], гл. IV, № 778–782; [6], гл. 14, № 208–213 |
Примечание. Ссылки на литературу в таблице даны в соответствии с номерами
в списке рекомендуемой литературы.
Справочный материал по теме "Интегральное
исчисление функции одной переменной"
Первообразная и неопределенный интеграл. Таблица интегралов
Функция F(x) называется первообразной для функции f(x) на интервале (a, b), если для всех x из этого интервала выполняется равенство
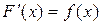 . (1)
. (1)
Неопределенным интегралом от функции f(x) называется множество всех первообразных этой функции, то есть неопределенный интеграл – это выражение вида 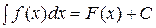 , где
, где 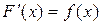 .
.
Процедуру нахождения неопределенного интеграла называют интегрированием. При интегрировании используют: таблицу интегралов (табл. 2), свойства интегралов и специальные методы интегрирования, основные
из которых – замена переменной и интегрирование по частям.
Таблица 2
1.  ; 2. ; 2. 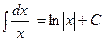 ; 3. ; 3.  ; 4. ; 4. 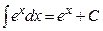 ; 5. ; 5. 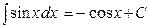 ; 6. ; 6.  ; 7. ; 7. 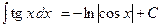 ; 8. ; 8. 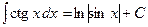 ; 9. ; 9.  ; ; | 10. 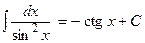 ; 11. ; 11.  ; 12. ; 12. 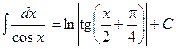 ; 13. ; 13. 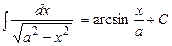 ; 14. ; 14. 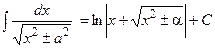 ; 15. ; 15.  ; 16. ; 16. 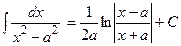 . . |
2. Свойства неопределенного интеграла.
Замена переменной под знаком неопределенного интеграла
При интегрировании функций наиболее часто используются следующие его свойства:
1) 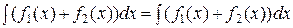 ;
;
2) 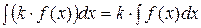 ;
;
3) 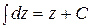 .
.
Пример 1. Найти 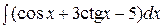 .
.
Решение. Воспользуемся свойствами 1–3, а также таблицей интегралов:
 =
=  + 3
+ 3 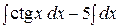 =
= 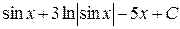 .
.
Ответ: 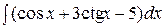 =
=  .
.
Одним из основных методов интегрирования является метод замены переменной (метод подстановки), который в некоторых случаях позволяет свести заданный интеграл к табличному интегралу.
Замена переменной под знаком неопределенного интеграла осуществляется по формулам:

или
 . (2)
. (2)
Пример 2. Найти 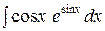 .
.
Решение. Воспользуемся формулой (2) и таблицей интегралов:
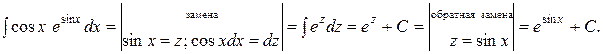
Ответ: 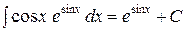 .
.
Этот интеграл можно взять, используя подведение под знак дифференциала части подинтегральной функции (не прописывая замену переменной)
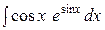 =
=  =
= 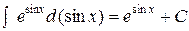 .
.
Наиболее часто прием подведения под знак дифференциала используется при линейной замене переменной интегрирования:
 , (3)
, (3)
так как  .
.
Пример 3. Найти  .
.
Решение. Согласно формуле (3) можно записать:
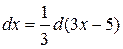
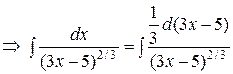 .
.
Теперь воспользуемся свойством 2, а также таблицей интегралов:
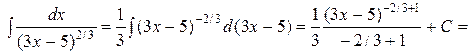
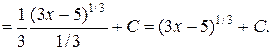
Ответ:  =
=  .
.
Интегрирование по частям
Формулой интегрирования по частям называют следующую формулу:
 . (4)
. (4)
Обычно за 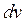 принимают такое выражение, интегрирование которого не вызывало бы трудностей, а за u – функцию, дифференцирование которой приводит к ее упрощению.
принимают такое выражение, интегрирование которого не вызывало бы трудностей, а за u – функцию, дифференцирование которой приводит к ее упрощению.
Можно выделить два основных класса интегралов, берущихся по частям:
1) 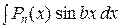 ;
;  ;
; 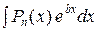 ;
; 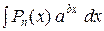
– здесь за u принимают целый многочлен 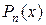 , за
, за  – оставшееся выражение, то есть, например
– оставшееся выражение, то есть, например  .
.
2)  ;
;  ;
; 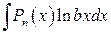
– здесь за u принимают обратную функцию, например, arcsinbx, за 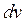 – оставшееся выражение, то есть
– оставшееся выражение, то есть  .
.
Интегрирование рациональных дробей
Рациональной дробью 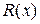 называют отношение двух целых многочленов
называют отношение двух целых многочленов 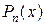 и
и 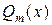 , т. е.
, т. е. 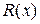 =
= 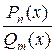 . Для интегрирования рациональной дроби необходимо предварительно разложить ее, т. е. представить
. Для интегрирования рациональной дроби необходимо предварительно разложить ее, т. е. представить 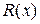 в виде суммы простейших дробей видов:
в виде суммы простейших дробей видов:
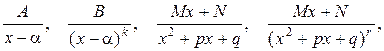
где k, r – целые положительные числа, а трехчлен  не имеет действительных корней.
не имеет действительных корней.
Если дробь 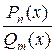 неправильная (
неправильная ( 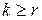 ), то необходимо предварительно выделить целую часть дроби.
), то необходимо предварительно выделить целую часть дроби.
