А) множество событий называется полной группой, если в результате испытания произойдет хотя бы одно из них

158.1. Два единственно возможных события, образующих полную группу, называются:

D) противоположными

159.1. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.

C)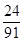

160.1. На склад поступило 100 тракторных дизелей. Из них 50 изготовлены за рубежом, остальные на Павлодарском тракторном заводе. Найти вероятность того, что взятый наудачу дизель изготовлен на Павлодарском тракторном заводе.

Е) 0,5

161.1. В ящике три стандартных и две нестандартных деталей. Наудачу отобрали 3 детали. Найти вероятность того, что среди отобранных деталей, окажется одна стандартная.

Е)

162.1. Для совместных событий А и В сумма вероятности Р(А+В) =

D) Р(А) +Р(В) – Р(АВ)

163.1. События называются несовместными, если:

D) P(A+B)=P(A)+P(B)

163.2. События называются совместными, если:

B) P(A+B)=P(A)+P(B)-P(AB)

164.1. Вероятность появления хотя бы одного из независимых событий А₁, А₂, …, А _n равна:

D) 1 - ×××

165.1. Известна вероятность р. Найти .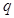

D)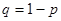

166.1. Вероятность того, что студент сдаст первый экзамен, равна 0,9, второй – 0,8. Найти вероятность того, что студентом будет сдан только второй экзамен.

С) 0,08

167.1. Указать формулу Бернулли.

D)

168.1. При каких условиях применяется формула Бернулли?

А) при небольшом числе испытаний

169.1. Законом распределения дискретной случайной величины называют

C) перечень её возможных значений и соответствующих вероятностей

170.1. На базу отправлено 4000 генераторов для автомобильного двигателя. Вероятность изготовления бракованного генератора равна 0,0005. Найти вероятность того, что прибудут три бракованных генератора.

А)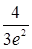

171.1. Математическое ожидание ДСВ (дискретной случайной величины) равно:

Е)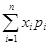

172.1. Средним квадратическим отклонением называется

А) квадратный корень из ее дисперсии

173.1. Число продаж Х автомашин в течение дня подчиняется следующему закону распределения

Х
Р	0,15	0,2	0,3	0,25	0,1

Найти математическое ожидание ежедневной продажи числа машин.

Е) 1,95

174.1. Число проданных компьютеров в течение дня подчиняется следующему закону распределения

Х
Р	0,15	0,1	0,1	0,25	0,4

Найти математическое ожидание ежедневной продажи числа компьютеров.

С) 2,65

175.1. Найти дисперсию Д(Х)?

Х
Р	0,1	0,5	0,3	0,1

D) 3,29

176.1. Найти дисперсию Д(Х)?

Х
Р	0,2	0,3	0,4	0,1

C) 2,01

177.1. 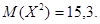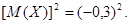Найти среднее квадратическое отклонение.

C) 3,9

178.1. Биномиальное распределение определяется формулой

А) Р(Х= ) =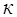

179.1. Плотностью распределения вероятностей непрерывной случайной величины называют

A) =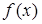

180.1. Случайная величина задана функцией распределения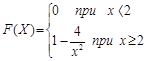

Найти плотность распределения.

А)

181.1. Вероятность того, что Х примет значение, принадлежащее интервалу ( :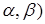

В) Р( 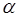< Х < ) =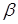

182.1. Статистическое распределение выборки устанавливает соответствие между: