Знаходження невідомих параметрів у разі завдання емпіричні формули у вигляді многочлен або показовою функції.

ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДЛЯ ПРАКТИЧНОЇ РОБОТИ

Методом найменших квадратів за даними таблиці знайти наближення у вигляді лінійної, квадратичної і показовою функцій. У кожному разі оцінити відхилення апроксимуючої функції від табличній в заданих точках, вказати функцію найкращого наближення.

Побудувати графіки функцій, знайдених методом найменших квадратів.

Варіанти завдань.

Варіант вибирається відповідно номера списку в журналі.

1)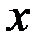
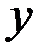		5,31	5,26	5,16	5,47	5,08

2)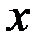
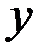		0,32	6,45	1,02	12,69	13,32

3)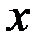
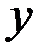		4,88	1,79	1,51	1,40	0,50

4)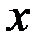
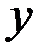		13,51	10,62	5,80	4,56	2,21

5)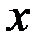
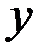		3,18	6,43	1,10	2,61	6,44

6)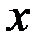
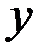		0,50	2,31	1,96	2,32	2,59

7)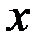
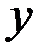		3,99	3,09	2,80	3,31	2,30

8)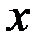
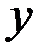		1,93	1,06	1,1	1,91	1,87

9)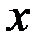
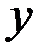		3,36	2,43	2,33	2,23	2,26

10)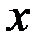
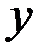		5,11	5,16	5,22	4,89	4,17

11)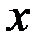
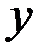		4,13	1,02	13,1	14,42	14,60

12)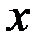
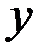		2,34	1,51	1,25	1,06	0,82

13)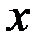
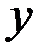		10,53	5,80	2,29	4,79	9,82

14)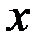
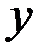		6,74	1,10	5,85	1,70	4,93

15)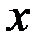
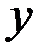		1,68	1,96	1,95	2,22	2,00

16)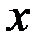
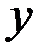		3,97	2,80	2,58	2,24	2,44

17)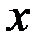
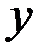		1,35	1,31	1,79	1,21	2,40

18)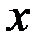
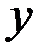		3,94	2,33	2,33	2,48	2,90

19)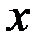
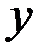		5,31	6,07	5,47	4,92	4,43

20)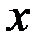
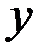		0,32	8,57	12,69	14,24	15,10

МЕТОД НАЙМЕНШИХ КВАДРАТІВ.

І. Теоретичні відомості

Нехай функція задана таблицею 2.1 і, як і раніше, потрібно побудувати функцію, що наближає табличну на заданому проміжку найкращим чином.

Крім побудови інтерполяційного многочлена існують і інші способи, один з яких без докладного пояснення, може бути вказаний. Це метод інтерполяційних або згладжують сплайнів. Сплайном називається функція, яка разом з кількома похідними неперервна на відрізку завдання функції, а на кожному окремому відрізку 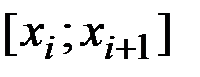є деяким алгебраїчним многочленом. Найчастіше використовуються кубічні сплайни, які беруть в вузлах 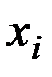значення .

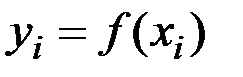Сплайни є більш зручним засобом апроксимації функцій на великих проміжках (при великих n), ніж інтерполяційний многочлен. Апроксимація функції на великому проміжку одним многочленом може значно збільшити ступінь многочлена, що на практиці неприйнятно.

Раніше зазначені методи застосовують не завжди, так як при побудові інтерполяційного полінома можлива чисельна нестійкість (тобто проміжні значення можуть суттєво відрізнятися від точок кривої). До того ж значення 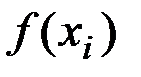можуть бути задані з похибками, можливими при отриманні досвідчених даних.

Для побудови сплайна потрібен великий обсяг обчислювальної роботи, результатом якої є функція, що має різний вигляд на різних ділянках, що не завжди зручно на практиці.

Принципово інший підхід методу найменших квадратів полягає в тому, щоб підібрати функцію 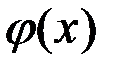, відхилення якої від досвідчених даних було б мінімальним серед всіх функцій даного виду. При цьому можливо точкове апроксимування функції на відрізку, якщо вихідні дані записані в таблицю, і інтегральне апроксимування функції на відрізку, якщо потрібно наблизити задану аналітичним виразом функцію деяким многочленом.

Мірою відхилення апроксимуючої функції 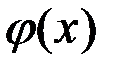від досвідчених даних 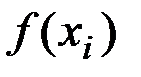є величина 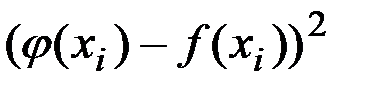, а мірою загальної помилки S є сума заходів відхилень для всіх дослідів, тобто

.

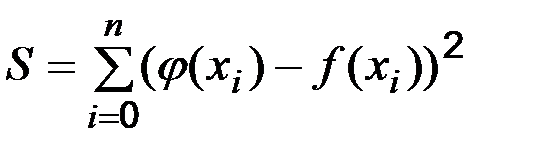Квадрати відхилень розглядають для того, щоб уникнути взаємного знищення окремих доданків великий величини і різних знаків.

Метод визначення констант, що входять в формулу 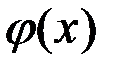шляхом мінімізації функції S називається методом найменших квадратів. Метод найменших квадратів націлений на зменшення найбільших відхилень. Формула 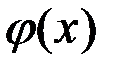, служить для аналітичного подання досвідчених даних, називається емпіричною.

Вид функції встановлений або з теоретичних міркувань, або на підставі характеру розташування на координатної площині точок, відповідних табличному значенню функції. Якщо вид емпіричної формули обраний, то виникає задача визначення параметрів, що входять в цю формулу, тобто

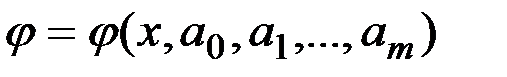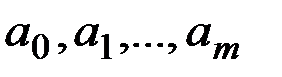, де - невідомі постійні.

Кількість цих констант вибирається зазвичай менше числа точок в таблиці.

Найкращими значеннями параметрів будуть ті, для яких сума заходів відхилень приймає найменше значення.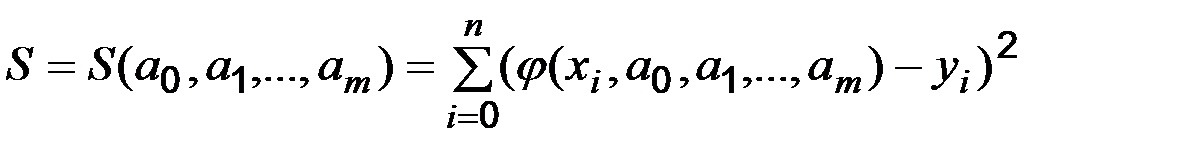

Якщо розглядається S як функція від 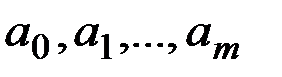, то очевидно, що 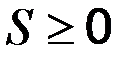і найменше значення цієї функції існує. Це можливо тільки в точці мінімуму функції S. Використовуючи необхідні умови екстремуму, отримуємо систему рівнянь для визначення параметрів .

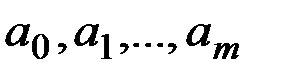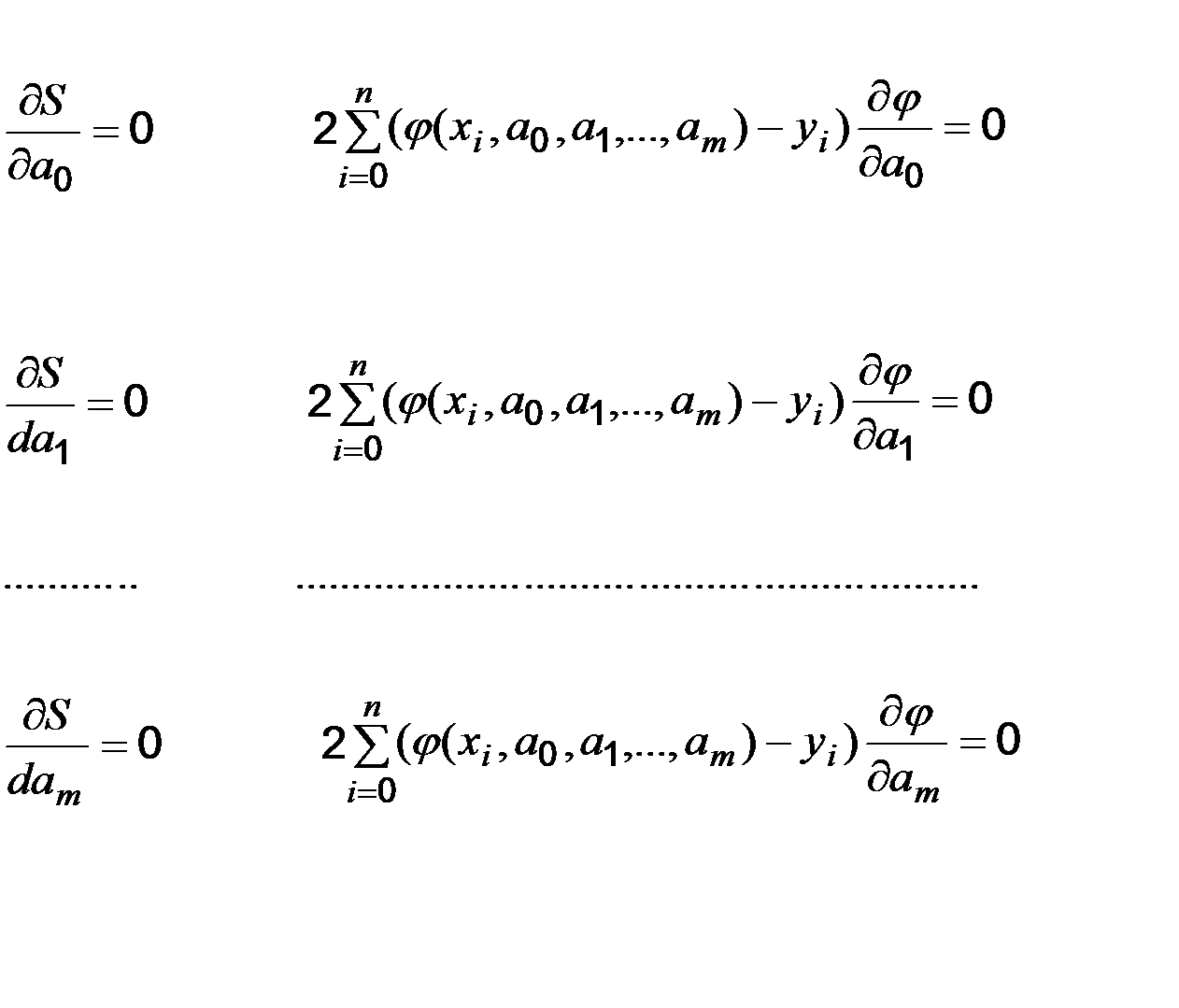
Якщо система має єдине рішення, то воно буде шуканим.

Як наближає функції в інженерних і економічних розрахунках часто використовується многочлен:

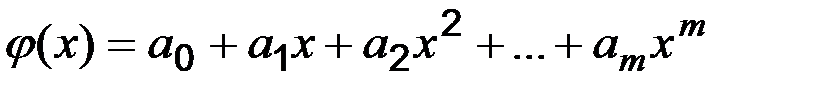
Якщо 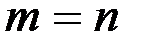, то апроксимуючий поліном збігається з поліномом Лагранжа ( при цьому ).

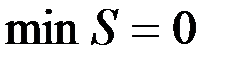Якщо залежність близька до періодичної, то апроксимація може бути задана тригонометричним многочленом.

Якщо емпірична формула обрана у вигляді показової функції 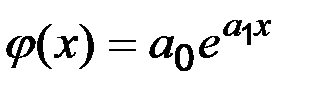, у вигляді степеневої 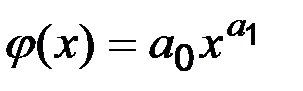, або у вигляді логарифмічної 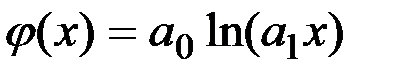, то позовними є тільки два параметри.

Формула, отримана методом найменших квадратів, називається рівнянням регресії, а відповідна крива - лінією регресії. Якщо в результаті обчислень отримано рівняння прямої лінії, то регресія називається лінійною, в іншому випадку - нелінійної.

Вихідні дані можуть мати найрізноманітніший характер і належати до різних галузей науки або техніки, наприклад

1) залежність тривалості служби електричних ламп 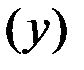від поданого на них напруги ;

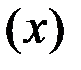2) залежність пробивної напруги конденсаторів 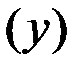від температури навколишнього середовища ;

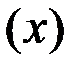3) залежність межі міцності стали 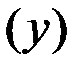від вмісту вуглецю ;

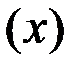4) залежність показників безробіття 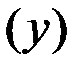та інфляції ;

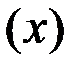5) залежність цін товару 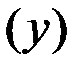від попиту 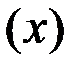на цей товар;

6) залежність приватного споживання 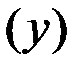від наявного доходу ;

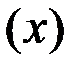та інші залежності.

ЗНАХОДЖЕННЯ НЕВІДОМИХ ПАРАМЕТРІВ У РАЗІ ЗАВДАННЯ ЕМПІРИЧНІ ФОРМУЛИ У ВИГЛЯДІ МНОГОЧЛЕН АБО ПОКАЗОВОЮ ФУНКЦІЇ.

Нехай в якості апроксимуючої функції обраний многочлен ступеня :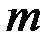

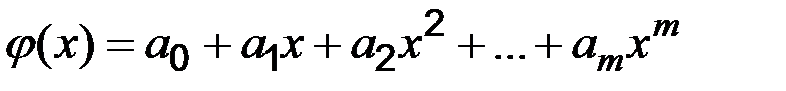
Толі сума квадратів відхилень має вигляд:

,

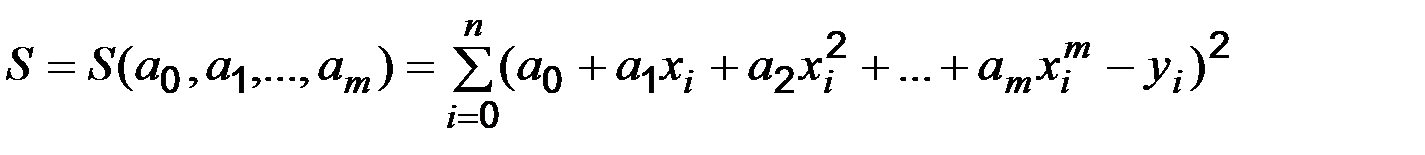а невідомі параметри будуть визначатися системою рівнянь: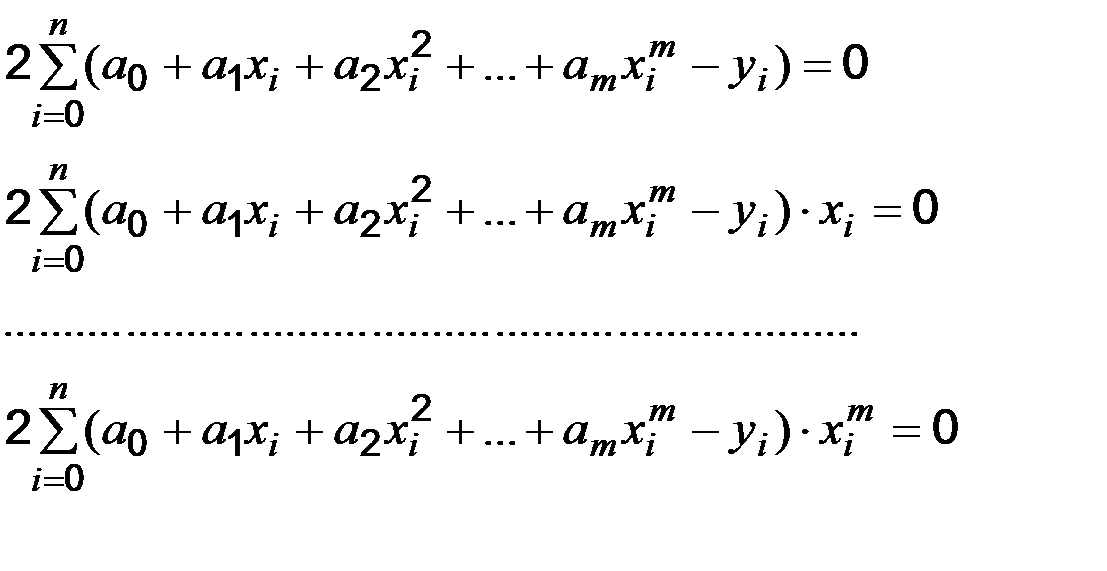

Якщо наближає функція 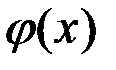обрана у вигляді показової функції 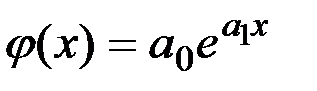, то вираз можна звести до лінійного, логарифмуючи ліву і праву частини рівності:

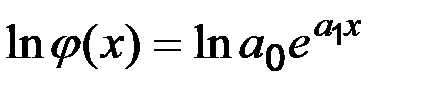або .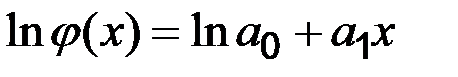

Після введення позначень: 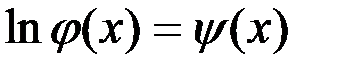, 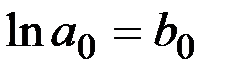; 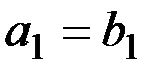, функція 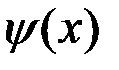записується як лінійна по аргументу :

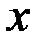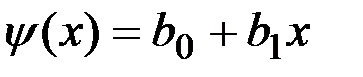
Сума відхилень визначається формулою:

,

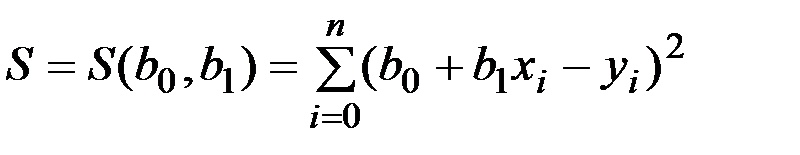А коефіцієнт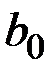и и 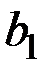знаходяться з розв’язку системи:

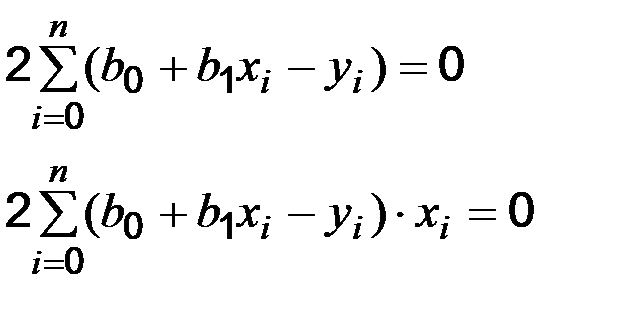
після чого здійснюється зворотний перехід до параметрів 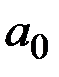і .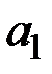

Аналогічно можна зробити і в тих випадках, коли в якості апроксимуючої функції обрані, наприклад, гіпербола 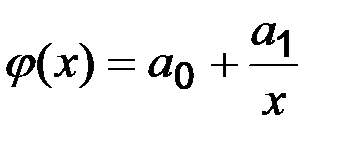або логарифмічна функція .

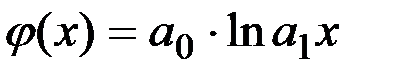ПРИКЛАД РОЗВЯЗАННЯ ЗАВДАННЯ:

ПРИКЛАДИ ПОБУДОВИ РІЗНИХ ВИДІВ АПРОКСИМУЮЧОЇ ФУНКЦІЇ.

Нехай функція задана таблицею 3.1. Потрібно побудувати методом найменших квадратів функцію, що наближає табличну найкращим чином. Для зручності позначень змінимо нумерацію вихідних даних і будемо вважати, що 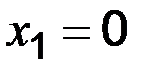; ; 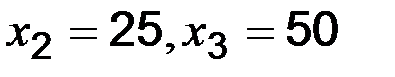; ; 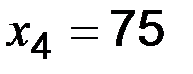; ; 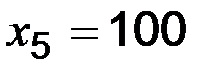; ; 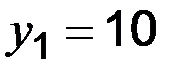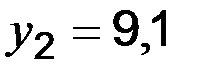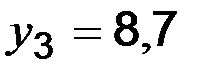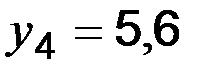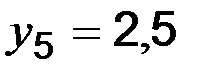. Зробимо припущення щодо характеру апроксимуючої функції, розглянувши розташування точок, заданих таблицею, на графіку (рис. 1.). (можна будувати точковий, а можна звичайний графік по даним)

Рис.1. Вихідні дані

За характером розташування точок на графіку можна висунути припущення про лінійну квадратичної або показовою залежності величин. Розглянемо всі три припущення.

Випадок 1. Будемо шукати наближену функцію 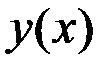у вигляді лінійної функції .

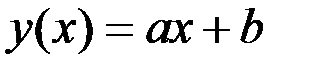Сума заходів відхилень 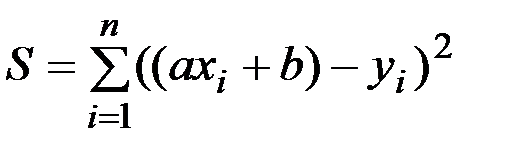, где 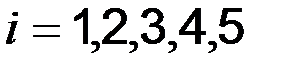; 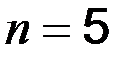- число вимірювань.

Знайдемо невідомі коефіцієнти із системи:

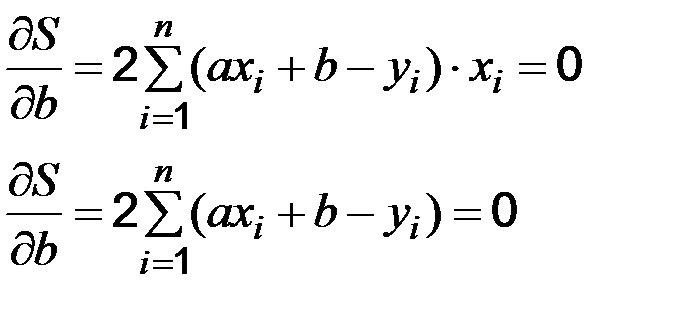
Після перетворення система приймає вигляд:

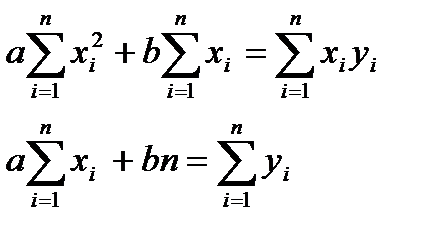… (1)

Складемо допоміжну таблицю

Таблиця 6.1.

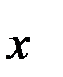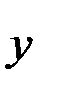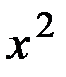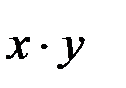		9,1		227,5
		8,7
		5,6
		2,5
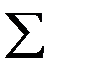		35,9		1332,5

Підставивши дані з таблиці 6.1 в систему (1), отримаємо: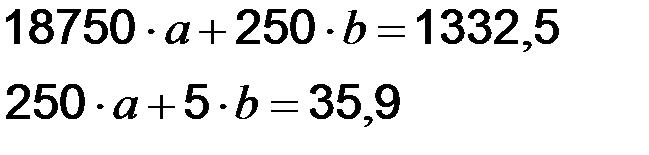

(систему розв’язувати методом Крамера)

Розрахунок можна робити у різних програмах таких як MatLab, MatCAD або Excel, який є найпростішою і найдоступнішою програмою)